The n-Category Café

Eric Drexler likes to say: engineering is dual to science, because science tries to understand what the world does, while engineering is about getting the world to do what you want. I think we need a slightly less ‘coercive’, more ‘cooperative’ approach to the world in order to develop ‘ecotechnology’, but it’s still a useful distinction.

For example, classical mechanics is the study of what things do when they follow Newton’s laws. Control theory is the study of what you can get them to do.

Say you have an upside-down pendulum on a cart. Classical mechanics says what it will do. But control theory says: if you watch the pendulum and use what you see to move the cart back and forth correctly, you can make sure the pendulum doesn’t fall over!

Control theorists do their work with the help of ‘signal-flow diagrams’. For example, here is the signal-flow diagram for an inverted pendulum on a cart:

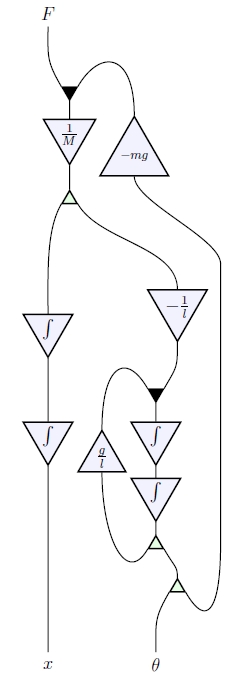
When I take a look at a diagram like this, I say to myself: that’s a string diagram for a morphism in a monoidal category! And it’s true. Jason Erbele wrote a paper explaining this. Independently, Bonchi, Sobociński and Zanasi did some closely related work:

• John Baez and Jason Erbele, Categories in control.

• Filippo Bonchi, Paweł Sobociński and Fabio Zanasi, Interacting Hopf algebras.

• Filippo Bonchi, Paweł Sobociński and Fabio Zanasi, A categorical semantics of signal flow graphs.

Next week I’ll explain some of the ideas at the Turin meeting on the categorical foundations of network theory. But I also want to talk about this new paper that Simon Wadsley of Cambridge University wrote with my student Nick Woods:

• Simon Wadsley and Nick Woods, PROPs for linear systems.

This makes the picture neater and more general!

You see, Jason and I used signal flow diagrams to give a new description of the category of finite-dimensional vector spaces and linear maps. This category plays a big role in the control theory of linear systems. Bonchi, Sobociński and Zanasi gave a closely related description of an equivalent category, $\mathrm{Mat}(k),$ where:

• objects are natural numbers, and

• a morphism $f : m \to n$ is an $n \times m$ matrix with entries in the field $k,$

and composition is given by matrix multiplication.

But Wadsley and Woods generalized all this work to cover $\mathrm{Mat}(R)$ whenever $R$ is a commutative rig. A rig is a ‘ring without negatives’—like the natural numbers. We can multiply matrices valued in any rig, and this includes some very useful examples… as I’ll explain later.

Wadsley and Woods proved:

Theorem. Whenever $R$ is a commutative rig, $\mathrm{Mat}(R)$ is the PROP for bicommutative bimonoids over $R.$

This result is quick to state, but it takes a bit of explaining! So, let me start by bringing in some definitions.

Bicommutative bimonoids

We will work in any symmetric monoidal category, and draw morphisms as string diagrams.

A commutative monoid is an object equipped with a multiplication:

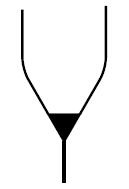
and a unit:

obeying these laws:

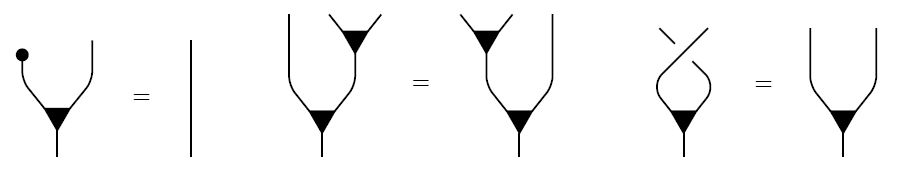
For example, suppose $\mathrm{FinVect}_k$ is the symmetric monoidal category of finite-dimensional vector spaces over a field $k$, with direct sum as its tensor product. Then any object $V \in \mathrm{FinVect}_k$ is a commutative monoid where the multiplication is addition:

$(x,y) \mapsto x + y$

and the unit is zero: that is, the unique map from the zero-dimensional vector space to $V.$

Turning all this upside down, cocommutative comonoid has a comultiplication:

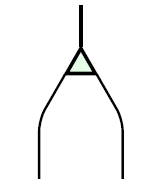
and a counit:

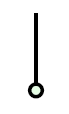
obeying these laws:

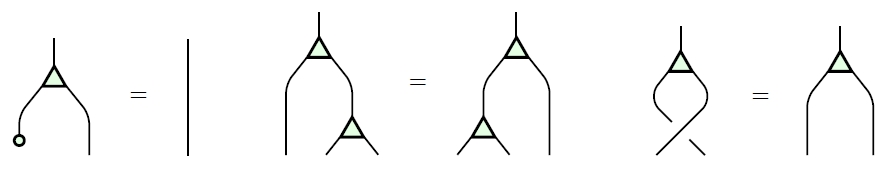
For example, consider our vector space $V \in \mathrm{FinVect}_k$ again. It’s a commutative comonoid where the comultiplication is duplication:

$x \mapsto (x,x)$

and the counit is deletion: that is, the unique map from $V$ to the zero-dimensional vector space.

Given an object that’s both a commutative monoid and a cocommutative comonoid, we say it’s a bicommutative bimonoid if these extra axioms hold:

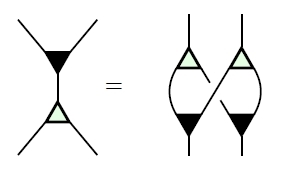
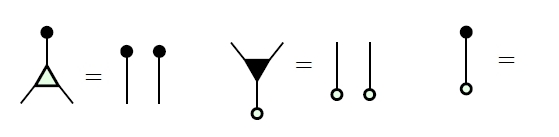
You can check that these are true for our running example of a finite-dimensional vector space $V.$ The most exciting one is the top one, which says that adding two vectors and then duplicating the result is the same as duplicating each one, then adding them appropriately.

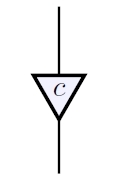
Our example has some other properties, too! Each element $c \in k$ defines a morphism from $V$ to itself, namely scalar multiplication by $c:$

$x \mapsto c x$

We draw this as follows:

These morphisms are compatible with the ones so far:

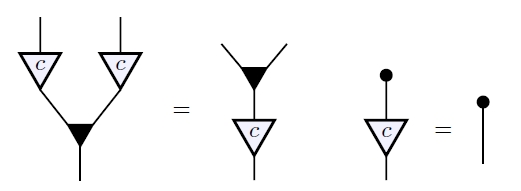
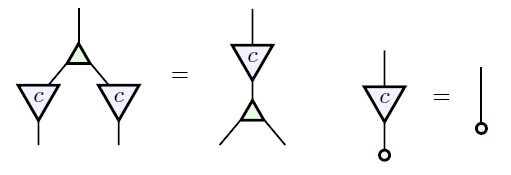
Moreover, all the ‘rig operations’ in $k$—that is, addition, multiplication, 0 and 1, but not subtraction or division—can be recovered from what we have so far:

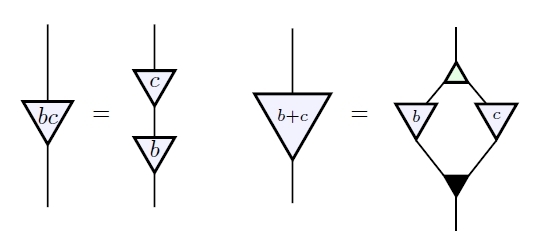
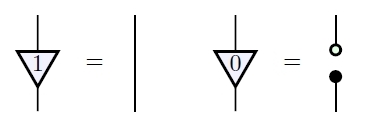
We summarize this by saying our vector space $V$ is a bicommutative bimonoid ‘over $k$’.

More generally, suppose we have a bicommutative bimonoid $A$ in a symmetric monoidal category. Let $\mathrm{End}(A)$ be the set of bicommutative bimonoid homomorphisms from $A$ to itself. This is actually a rig: there’s a way to add these homomorphisms, and also a way to ‘multiply’ them (namely, compose them).

Suppose $R$ is any commutative rig. Then we say $A$ is a bicommutative bimonoid over $R$ if it’s equipped with a rig homomorphism

$\Phi : R \to \mathrm{End}(A)$

This is a way of summarizing the diagrams I just showed you! You see, each $c \in R$ gives a morphism from $A$ to itself, which we write as

The fact that this is a bicommutative bimonoid endomorphism says precisely this:

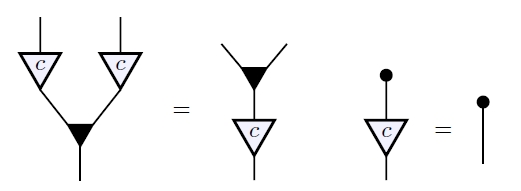
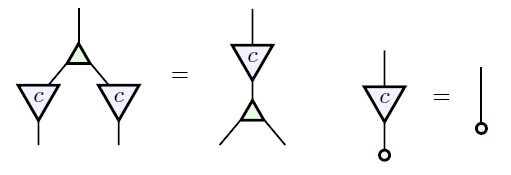
And the fact that $\Phi$ is a rig homomorphism says precisely this:

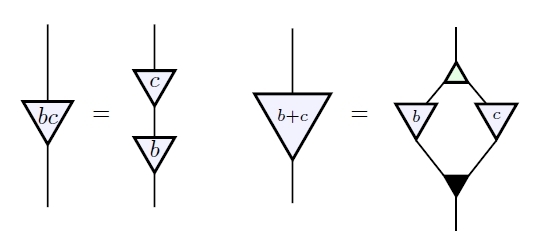
So sometimes the right word is worth a dozen pictures!

What Jason and I showed is that for any field $k,$ the $\mathrm{FinVect}_k$ is the free symmetric monoidal category on a bicommutative bimonoid over $k.$ This means that the above rules, which are rules for manipulating signal flow diagrams, completely characterize the world of linear algebra!

Bonchi, Sobociński and Zanasi used ‘PROPs’ to prove a similar result where the field is replaced by a sufficiently nice commutative ring. And Wadlsey and Woods used PROPS to generalize even further to the case of an arbitrary commutative rig!

But what are PROPs?

PROPs

A PROP is a particularly tractable sort of symmetric monoidal category: a strict symmetric monoidal category where the objects are natural numbers and the tensor product of objects is given by ordinary addition. The symmetric monoidal category $\mathrm{FinVect}_k$ is equivalent to the PROP $\mathrm{Mat}(k),$ where a morphism $f : m \to n$ is an $n \times m$ matrix with entries in $k,$ composition of morphisms is given by matrix multiplication, and the tensor product of morphisms is the direct sum of matrices.

We can define a similar PROP $\mathrm{Mat}(R)$ whenever $R$ is a commutative rig, and Wadsley and Woods gave an elegant description of the ‘algebras’ of $\mathrm{Mat}(R)$. Suppose $C$ is a PROP and $D$ is a strict symmetric monoidal category. Then the category of algebras of $C$ in $D$ is the category of strict symmetric monoidal functors $F : C \to D$ and natural transformations between these.

If for every choice of $D$ the category of algebras of $C$ in $D$ is equivalent to the category of algebraic structures of some kind in $D,$ we say $C$ is the PROP for structures of that kind. This explains the theorem Wadsley and Woods proved:

Theorem. Whenever $R$ is a commutative rig, $\mathrm{Mat}(R)$ is the PROP for bicommutative bimonoids over $R.$

The fact that an algebra of $\mathrm{Mat}(R)$ is a bicommutative bimonoid is equivalent to all this stuff:

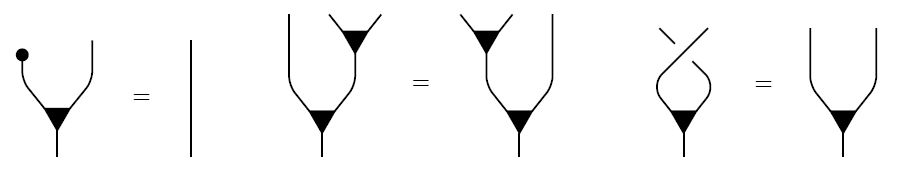
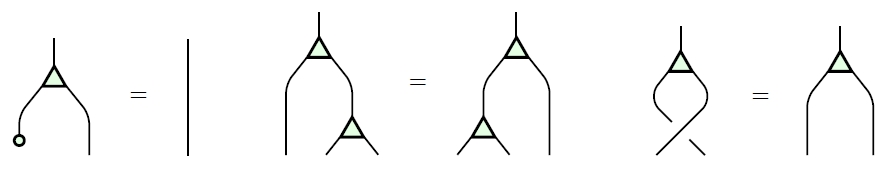
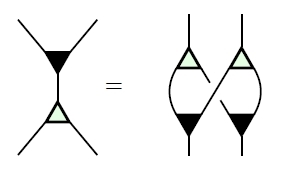
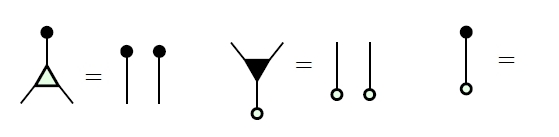
The fact that $\Phi(c)$ is a bimonoid homomorphism for all $c \in R$ is equivalent to this stuff:

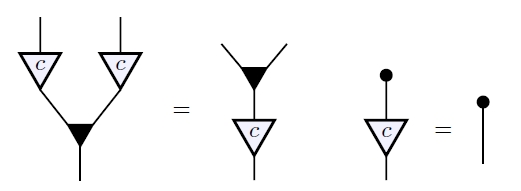
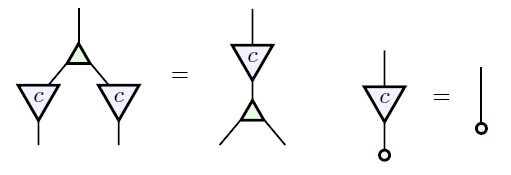
And the fact that $\Phi$ is a rig homomorphism is equivalent to this stuff:

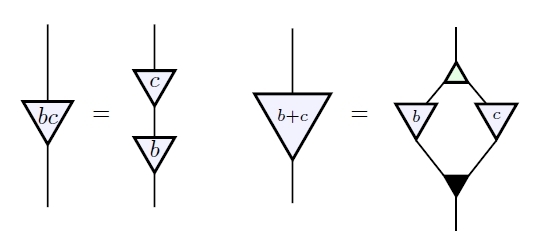
This is a great result because it includes some nice new examples.

First, the commutative rig of natural numbers gives a PROP $\mathrm{Mat}.$ This is equivalent to the symmetric monoidal category $\mathrm{FinSpan},$ where morphisms are isomorphism classes of spans of finite sets, with disjoint union as the tensor product. Steve Lack had already shown that $\mathrm{FinSpan}$ is the PROP for bicommutative bimonoids. But this also follows from the result of Wadsley and Woods, since every bicommutative bimonoid $V$ is automatically equipped with a unique rig homomorphism

$\Phi : \mathbb{N} \to \mathrm{End}(V)$

Second, the commutative rig of booleans

$\mathbb{B} = \{F,T\}$

with ‘or’ as addition and ‘and’ as multiplication gives a PROP $\mathrm{Mat}(\mathbb{B}).$ This is equivalent to the symmetric monoidal category $\mathrm{FinRel}$ where morphisms are relations between finite sets, with disjoint union as the tensor product. Samuel Mimram had already shown that this is the PROP for special bicommutative bimonoids, meaning those where comultiplication followed by multiplication is the identity:

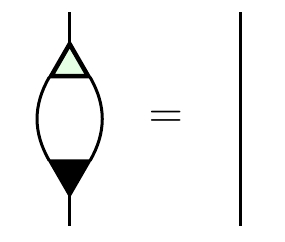
But again, this follows from the general result of Wadsley and Woods!

Finally, taking the commutative ring of integers $\mathbb{Z},$ Wadsley and Woods showed that $\mathrm{Mat}(\mathbb{Z})$ is the PROP for bicommutative Hopf monoids. The key here is that scalar multiplication by $-1$ obeys the axioms for an antipode—the extra morphism that makes a bimonoid into a Hopf monoid. Here are those axioms:

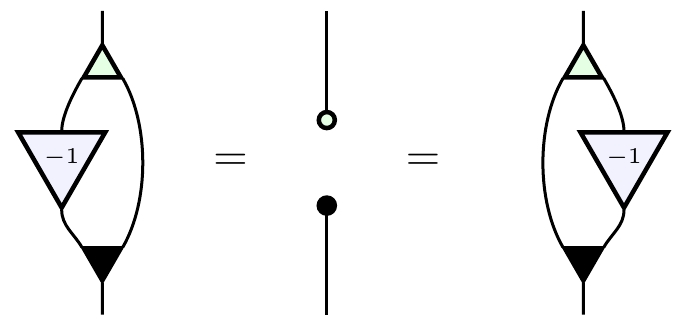
More generally, whenever $R$ is a commutative ring, the presence of $-1 \in R$ guarantees that a bimonoid over $R$ is automatically a Hopf monoid over $R.$ So, when $R$ is a commutative ring, Wadsley and Woods’ result implies that $\mathrm{Mat}(R)$ is the PROP for Hopf monoids over $R.$

Earlier, in their paper on ‘interacting Hopf algebras’, Bonchi, Sobociński and Zanasi had given an elegant and very different proof that $\mathrm{Mat}(R)$ is the PROP for Hopf monoids over $R$ whenever $R$ is a principal ideal domain. The advantage of their argument is that they build up the PROP for Hopf monoids over $R$ from smaller pieces, using some ideas developed by Steve Lack. But the new argument by Wadsley and Woods has its own charm.

In short, we’re getting the diagrammatics of linear algebra worked out very nicely, providing a solid mathematical foundation for signal flow diagrams in control theory!