The n-Category Café

The homotopy coherent nerve

By familiar abstract nonsense, the adjunction $ℂ⊣\mathbb{N}$ is uniquely determined by a functor Δ$\to$sSet-Cat, which sends each object $[n]$ of Δ $\subset$Cat to a simplicial category $ℂ{\Delta }^n$. The simplicial category $ℂ{\Delta }^n$ is a cofibrant replacement of the trivial simplicial category structure on the poset category $[n]$ and has the same objects 0, 1, $\dots$, $n$. Its hom-spaces are typically defined to be nerves of certain poset categories, but we prefer an alternate description.

There is a free-forgetful adjunction $F:$rGrph$\leftrightarrow$Cat$:U$ between small categories and reflexive graphs, which are directed graphs equipped with an identity edge at each vertex. This adjunction induces a comonad $\mathrm{FU}$ on Cat and the resulting comonad resolution defines a simplicial object in Cat

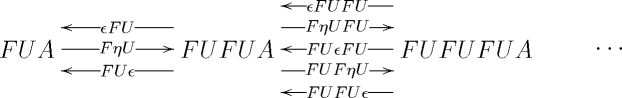
for any (ordinary) small category $A$. A simplicial object in Cat gives rise to a simplicial category if and only if all of the functors involved are identities on objects, which is the case here. The $n$-simplices of the hom-object from $a$ and $b$ are the morphisms from hom-set $(FU{)}^{n+1}A(a,b)$.

Unraveling the definition, the 0-simplices of this simplicial category are strings of composable non-identity morphisms in $A$; the 1-simplices are strings of morphisms where every morphism appears in exactly one set of parentheses; the 2-simplices are strings where every morphism appears in exactly two sets of parentheses; and so forth. The face maps $(FU{)}^kϵ(FU{)}^j$ remove the parentheses that are contained in exactly $k$ others; $FU\cdots FUϵ$ composes the morphisms inside the innermost parentheses. The degeneracy maps $F(UF{)}^k\eta (UF{)}^{j}U$ double up the parentheses that are contained in exactly $k$ others; $F\cdots UF\eta U$ inserts parentheses around each individual morphism.

When we let $A$ be the poset category $[n]$, the simplicial category arising from this comonad resolution is $ℂ{\Delta }^n$, as usually defined. For example, let’s compute the hom-object $ℂ{\Delta }^3(0,3)$ for the simplicial category associated to the poset category $[3]$ with objects 0, 1, 2, 3 and morphisms as shown

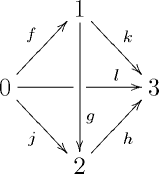
Examining the morphisms of $FU[3]$ from 0 to 3 we see there are four 0-simplices: $l$, $hj$, $kf$, and $hgf$. Similarly, examining $FUFU[3]$ reveals nine 1-simplices - $(hgf)$, $(hg)(f)$, $(h)(gf)$, $(hj)$, $(kf)$, $(h)(g)(f)$, $(h)(j)$, $(k)(f)$, and $(l)$ - the last four of which are degenerate. Finally, examining $FUFUFU[3]$ reveals two non-degenerate 2-simplices $((hg)(f))$ and $((h)(gf))$ with boundary as indicated

together with 14 degenerate ones. There are no non-degenerate higher simplices. Hence, $ℂ{\Delta }^3(0,3)={\Delta }^1\times {\Delta }^1$.

In general, the hom-object $ℂ{\Delta }^n(i,j)$ is empty if $i>j$, a point if $i=j$, and the cube $({\Delta }^1{)}^{j-i-1}$ when $i<j$.

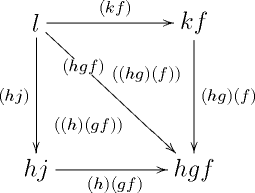
The homotopy coherent nerve of a simplicial category $C$ is the simplicial set with $\mathbb{N}{C}_n=$ sSet-Cat$(ℂ{\Delta }^n,C)$. So, for example, the data of a 3-simplex in the homotopy coherent nerve of $C$ consists of four objects $x$, $y$, $z$, $w$ of $C$; 6 vertices $f\in C(x,y{)}_0$, $g\in C(y,z{)}_0$, $h\in C(z,w{)}_0$, $j\in C(x,z{)}_0$, $k\in C(y,w{)}_0$, and $l\in C(x,w{)}_0$; 1-simplices $j\to gf$, $k\to hg$, $l\to hj$, $l\to kf$, $l\to hgf$ (where the new vertices are defined using the horizontal composition of $C$); and two 2-simplices in $C(x,w)$ whose boundary edges are depicted below.

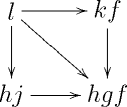
Understanding the hom-spaces of $ℂX$

Now let’s turn our attention to the left adjoint $ℂ$. Let $X$ be a simplicial set. By definition

$$ℂX={\int }^{[n]\in \Delta }\coprod _{X_n}ℂ{\Delta }^n.$$

Morally,

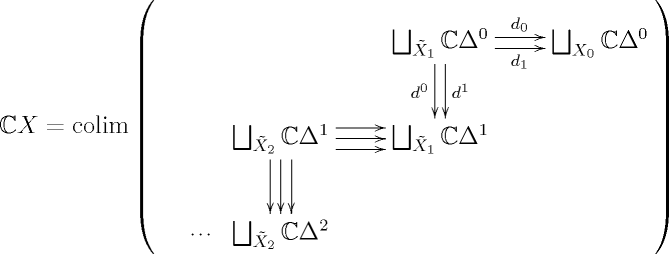
where ${\tilde{X}}_n$ denotes the non-degenerate $n$-simplices of $X$.

The objects of $ℂX$ are the vertices of $X$. The simplicial categories $ℂ{\Delta }^0$ and $ℂ{\Delta }^1$ are the free simplicial categories on the poset categories $[0]$ and $[1]$ respectively, and the free simplicial category functor is a left adjoint and so commutes with colimits. Hence, if $X$ is 1-skeletal so that ${\tilde{X}}_n=\varnothing$ for all $n>1$, then $ℂX$ is the free simplicial category on the graph with vertex set $X_0$ and edge set ${\tilde{X}}_1$. Concretely, this means that the hom-spaces $ℂX(x,y)$ are all discrete simplicial sets containing a vertex for each path of edges from $x$ to $y$ in $X$.

In general, for each 2-simplex of $X$ with 2nd face $f$, 0th face $g$, and 1st face $j$, there exists a 1-simplex from the vertex $j$ to the vertex $gf$ in $ℂX(x,y)$. Furthermore, for each vertex in some hom-space representing a sequence of paths containing $j$, there is a 1-simplex connecting it to the vertex representing the same sequence, except with $gf$ in place of $j$.

However, the 2-skeleton of $X$ does not determine the 1-skeleta of the hom-spaces. For example, for each 3-simplex of $X$ as depicted by (1), there is an edge from $l$ to $hgf$ in $ℂX(x,y)$. In general, there is an edge between the vertices represented by paths $p_1\dots p_r$ and $q_1\dots q_r$ of edges from $x$ to $y$ in $X$ if and only if each edge $p$ in the first path that does not appear in the second is replaced by a sequence of $n$-edges that appear as the spine of some $n$-simplex of $X$ with $p$ as its diagonal. Here, the spine of an $n$-simplex is the sequence of edges between the adjacent vertices, using the usual ordering of the vertices, and the diagonal is the edge $[0,n]$ from the initial vertex to the final one.

In this way, each edge of $ℂX(x,y)$ corresponds to a necklace ${\Delta }^{n_1}\vee \cdots \vee {\Delta }^{n_r}\to X$ in $X$, where ${\Delta }^n\vee {\Delta }^k$ means that the final vertex of the $n$-simplex is identified with the initial vertex of the $k$-simplex, and the initial and final vertices of the necklace map to $x$ and $y$ respectively. A necklace is comprised of a sequence of beads, the ${\Delta }^{n_i}$ above, that are strung together along the joins, defined to be the union of the initial and final vertices of each bead.

The necklace characterization

By a theorem of Dugger and Spivak, necklaces can be used to characterize the higher dimensional simplices of the hom-spaces $ℂX(x,y)$ as well, provided we keep track of additional vertex data.

Theorem (DS) Let $X$ be a simplicial set with vertices $x$ and $y$. An $n$-simplex in $ℂX(x,y)$ is uniquely represented by a triple $(T,f,\stackrel{\rightharpoonup }{T})$, where $T$ is a necklace; $f:T\to X$ is a map of simplicial sets that sends each bead of $T$ to a non-degenerate simplex of $X$ and the endpoints of the necklace to the vertices $x$ and $y$ respectively; and $\stackrel{\rightharpoonup }{T}$ is a flag of sets $$J_T=T^0\subset T^1\subset T^2\subset \cdots \subset T^{n-1}\subset T^n=V_T$$ of vertices $V_T$ of $T$, where $J_T$ is the set of joins of $T$.

Necklaces $f:T\to X$ with the property described above are called totally non-degenerate. Note that the map $f$ need not be injective. If $x=y$ is a vertex with a non-degenerate edge $e$, the map $e:{\Delta }^1\to X$ defines a totally non-degenerate necklace in $X$.

Importantly, the face maps $d_i:ℂX(x,y{)}_n\to ℂX(x,y{)}_{n-1}$ can also be described in the language of flags and necklaces. When $0<i<n$, $d_i(T,f,\stackrel{\rightharpoonup }{T})=(T,f,d_i\stackrel{\rightharpoonup }{T})$ where $d_i\stackrel{\rightharpoonup }{T}$ is the flag of sets $J_T\subset \cdots \subset \widehat{T^i}\subset \cdots \subset V_T$ with $T^i$ removed from the sequence.

To compute $d_n$, restrict $T$ to the subnecklace $T\prime =T{\mid }_{T^{n-1}}$ with vertices $T^{n-1}$. If the triple $(T\prime ,f{\mid }_{T\prime },d_n\stackrel{\rightharpoonup }{T})$ is totally non-degenerate, this is the $n$th face. Otherwise, there exists a unique quotient $(\overline{T\prime },\overline{f})$ of $(T\prime ,f{\mid }_{T\prime })$ that is totally non-degenerate, and $d_n(T,f,\stackrel{\rightharpoonup }{T})=(\overline{T\prime },\overline{f},\overline{d_n\stackrel{\rightharpoonup }{T}})$, where $\overline{d_n\stackrel{\rightharpoonup }{T}}$ is the image of $d_n\stackrel{\rightharpoonup }{T}$ under the surjection $T\prime \to \overline{T\prime }$.

To compute $d_0$, break up the beads of $T$ along the vertices in $T^1$ to form a necklace $T^{″}\subset T$ with joins $T^1$; we call this the $T^1$-splitting of $T$. If $(T^{″},f{\mid }_{T^{″}},d_0\stackrel{\rightharpoonup }{T})$ is totally non-degenerate, this is the 0th face. Otherwise, $d_0(T,f,\stackrel{\rightharpoonup }{T})=(\overline{T^{″}},\overline{f},\overline{d_0\stackrel{\rightharpoonup }{T}})$, the unique totally non-degenerate quotient, as above.

For example, let’s take $X={\Delta }^3$ and recompute $ℂ{\Delta }^3(0,3)$. The vertices are necklaces whose set of joins must equal the set of vertices. These necklaces necessarily have the form ${\Delta }^1\vee \cdots \vee {\Delta }^1$ and are in bijective correspondence with paths of 1-simplices from 0 to 3, as above.

The 1-simplices of $ℂ{\Delta }^3(0,3)$ are precisely the non-degenerate necklaces of ${\Delta }^3$ from 0 to 3. They have shapes ${\Delta }^3$, ${\Delta }^1\vee {\Delta }^2$, ${\Delta }^2\vee {\Delta }^1$, ${\Delta }^2$ (mapping to the 2-simplex $d^1$), ${\Delta }^2$ (mapping to the 2-simplex $d^2$), ${\Delta }^1\vee {\Delta }^1\vee {\Delta }^1$, ${\Delta }^1\vee {\Delta }^1$, ${\Delta }^1\vee {\Delta }^1$, and ${\Delta }^1$, where these are listed in the same order given above (2).

Non-degenerate 2-simplices are necklaces together with a subset of vertices that strictly contains the set of joins. There are only two such, both with shape ${\Delta }^3$ and flags $\{0,3\}\subset \{0,1,3\}\subset [3]$ or $\{0,3\}\subset \{0,2,3\}\subset [3]$. It is a good exercise to compute the boundaries of these two 2-simplices to see which is which.

Applications

To my mind, a main selling point of the necklace characterization is that it makes it easy to compute the simplicial category associated to a generic simplicial set. (Exercise: compute the simplicial category $ℂ{\Lambda }_k^n$ associated to the $(n,k)$-horn.) Even better, it allows us to easily prove a number of theorems.

The first result, describing the cofibrant replacement of an ordinary category regarded as a simplicial category with discrete hom-objects, might be known already, but I can’t find a reference. (Please tell me if you know one!)

Theorem. For any ordinary category $A$, the simplicial category $ℂNA$ is equal to the simplicial category constructed by the comonad resolution described above (where $N$ is the ordinary nerve).

Proof: A necklace in a category is uniquely determined by its spine and the set of joins. An $n$-simplex in the comonad resolution is a string of morphisms, each contained within $(n-1)$ sets of parentheses. The morphisms in the string describe the spine and the locations of each level of parentheses defines the corresponding set in the flag of vertex data. $\square$

When I started thinking about these things, I naively hoped that the simplicial categories associated to quasi-categories might have some fibrancy properties. Using the necklaces, we can prove:

Theorem. If $X$ is a quasi-category, any horn ${\Lambda }_1^2\to ℂX(x,y)$ has a filler.

Proof: Amalgamate the two necklaces given by the horn, and then extend the resulting simplicial set to a larger necklace containing the two. This will determine the missing face and also the filler.$\square$

However, for most quasi-categories $X$, indeed for all quasi-categories that are not themselves categories and then for many categories as well, there are some 3-dimensional inner horns (and likely also 4-dimensional horns) in some $ℂX(x,y)$ which cannot be filled. But in higher dimensions all horns (not necessarily inner) can be filled uniquely, as a consequence of the following Theorem, which really surprised me.

Theorem. For any simplicial set $X$, $ℂX(x,y)$ is 3-coskeletal.

This says that any sphere $\partial {\Delta }^n$ in $ℂX(x,y)$ with $n$ at least four can be filled uniquely. The proof is actually quite easy. The necklace of the unique filler to a sphere also represents each of the inner faces and when $n\ge 4$, the flags of these faces also define the flag of the filler. It remains to check that this filler is compatible with the outer faces, but this can be done by considering the appropriate spherical identity.

When $X$ is a category, the hom-objects of $ℂX$ are in fact 2-coskeletal. The main point of the proof is that the face map $d_0$ described in (3) is better behaved for necklaces in categories. Examples can be given to show that these results are all optimal, but I suspect I’ve said quite enough already.