An Adventure in Analysis
Posted by Tom Leinster
One reason I went into category theory is that I wanted a subject that would take me to different parts of the mathematical world. These last few weeks I’ve been getting my wish in spades. My hard drive contains 53 analysis papers and books that three weeks ago it didn’t. My desk is piled with library books. My floor is a mess of handwritten notes covered in integral signs.
What prompted this adventure in analysis was a problem about magnitude of metric spaces. Thanks to the contributions of a whole crowd of people, the problem has now been solved. The problem-solving process, here and at Math Overflow, took all sorts of twists and turns, many of them unnecessary. But I think I can now present a fairly straight path to a solution. To thank those who contributed — and to entertain those who were half-interested but didn’t have the energy to keep up — I give you an overview of the problem and its solution.
Background Let be a finite metric space. The similarity matrix of is the matrix . If is invertible, we define the magnitude (or cardinality) of to be the sum of all entries of .
(There are known to be metric spaces whose similarity matrix is not invertible. Magnitude can be sensibly defined under a weaker hypothesis than invertibility of ; but still, it is not always defined.)
A finite metric space is positive definite if is positive definite: that is, for all , with equality only if . Positive definiteness turns out to be an important property for various reasons: see here, here, here or here (pp.12–14, 23–25). In essence: magnitude of metric spaces can behave in apparently weird ways, but not if you restrict to positive definite spaces. The positive definite spaces are the ‘non-weird’ ones.
In particular, since positive definite matrices are invertible, any positive definite space has a well-defined magnitude.
There are many well-known metrics on . For and , let denote equipped with the metric coming from the -norm , as a metric space: thus, The ‘taxicab’ metric () gets along very well with magnitude (ultimately because it comes from the tensor product of enriched categories). I’ve known for a long time that every finite subspace of is positive definite. In particular, the magnitude of every finite subspace of is well-defined.
But when I say that in seminars, no one cares! What everyone wants to know is whether the same is true for the Euclidean metric, . And if it’s true for and , what about ?
The problem Show that every finite subspace of is positive definite, for all and .
(There are good reasons for believing this to be false when .)
It will follow that every finite subpace of has well-defined magnitude. In particular:
Every finite subspace of , with the Euclidean metric, has well-defined magnitude.
Consequently, I lose a small bet against Simon Willerton.
The solution Here’s a 4-step outline of a proof. If you want more, you can read the detailed version that I wrote up. Much of it would be regarded as standard by (some) analysts. What I think is the hardest, or least standard, part of the proof is due to Mark Meckes. I’ll mention the other main contributors as we go along. Tell me if I’ve left you off!
Step 1: Find the connection with analysis It turns out that this type of problem has been studied in analysis since the 1920s or 30s. The key concept is that of ‘positive definite function’. David Corfield and Yemon Choi were the first to point this out. Of course, until you know the terminology you have no idea what to look up, so this kind of information is vital.
A function is positive definite if for all and , the matrix is positive semidefinite (that is, for all ). It is strictly positive definite if this same matrix is positive definite.
As you can see, there’s a terminological calamity here. An analyst friend tells me that many analysts call a real number ‘positive’ if it is . (I thought only the French did that.) Presumably the terminology above, which by now is well entrenched, comes from that tradition. I’ll call a real number positive iff it is .
Anyway, in this language the problem becomes:
The problem, version 2: Show that for each and , the real-valued function on is strictly positive definite.
Step 2: Harness the power of the Fourier transform We want to prove that something is strictly positive definite. The following sufficient condition will do it for us:
Let be a continuous, bounded, integrable function. If the Fourier transform of is everywhere positive then is strictly positive definite.
This result seems to be due to Holger Wendland, from a paper On the smoothness of positive definite and radial functions. David Speyer also found most of a proof of this (1, 2). It’s related to a result that’s well known in harmonic analysis, Bochner’s Theorem, but that’s about non-strict positive definiteness, which is what most people have concentrated on historically.
So, the problem reduces to:
The problem, version 3: Show that for and , the function on has everywhere positive Fourier transform.
If the Euclidean metric is all you care about, you can stop reading at the end of this sentence: for the Fourier transform of can be calculated explicitly (Stein and Weiss, Introduction to Fourier Analysis on Euclidean Spaces, page 6), and it’s everywhere positive.
Step 3: Crack the hard nut that is the -norm This step and the next are due to Mark Meckes, via Math Overflow. Parts of the argument are from the book Fourier Analysis in Convex Geometry by Alexander Koldobsky.
We have to think about the Fourier transform of the function on . If that th power weren’t there, life would be simpler, because we’d just have a product of exponentials. It is there — but in some sense, this step shows how to make it disappear.
We’ll see that the function can be re-expressed in a more convenient way. It is, in fact, an ‘infinite linear combination’, with nonnegative coefficients, of functions of the form . That is, there is a finite nonnegative measure on such that for all , The th power has gone!
For the cognoscenti, this follows by observing that the function is completely monotone, then applying Bernstein’s theorem.
(Koldobsky’s book calls it ‘the celebrated Bernstein’s Theorem’. Whenever anyone describes a theorem as ‘celebrated’, I imagine a party thrown in its honour, with streamers and balloons.)
Step 4: Put it all together Earlier, we reduced the problem to showing that, for and , the Fourier transform of the function on is everywhere positive.
The previous step showed how to re-express in a more convenient way.
Now: work out the Fourier transform of by using this re-expression. Following your nose, the problem reduces to:
The problem, version 4: Show that the Fourier transform of the function on is everywhere positive.
Do we have a formula for the Fourier transform of ? No, apparently not, except when or . But Lemma 2.27 of Koldobsky’s book tells us that it is indeed everywhere positive, and that’s all we need to know.

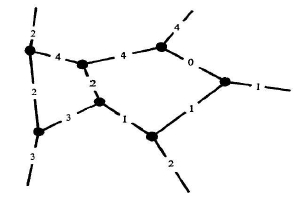 Now draw (on your own paper, because I haven't the skills to draw it nicely here) the dual diagram, which consists of (except at the edges) a bunch of triangles, and think of the labels on its edges as lengths. You'll see that each triangle is possible, in that its edges obey the triangle inequality (although many of them are degenerate and, even accounting for that, the diagram cannot be embedded in Euclidean space).
Now draw (on your own paper, because I haven't the skills to draw it nicely here) the dual diagram, which consists of (except at the edges) a bunch of triangles, and think of the labels on its edges as lengths. You'll see that each triangle is possible, in that its edges obey the triangle inequality (although many of them are degenerate and, even accounting for that, the diagram cannot be embedded in Euclidean space).
Re: An Adventure in Analysis
The fact the metric on , is positive SEMIdefinite is well known to functional analysts. See for example Chapter 8 of Benyamini and Lindenstraus [BL] here.
The connection to embedding also should help in proving that , , does not have this property: The property
is positive semidefinite for every ,
is called negative definite in [BL] and is equivalent to being isometrically embeddable in Hilbert space (Proposition 8.5 in [BL]). It is known that , is not negative definite, see for example theorems 1.10 and 1.11 in this paper.