Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

June 14, 2016

Coriolis

I really like the science fiction TV series The Expanse. In addition to a good plot and a convincing vision of human society two centuries hence, it depicts, as Phil Plait observes, a lot of good science in a matter-of-fact, almost off-hand fashion. But one scene (really, just a few dialogue-free seconds in a longer scene) has been bothering me. In it, Miller, the hard-boiled detective living on Ceres, pours himself a drink. And we see — as the whiskey slowly pours from the bottle into the glass — that the artificial gravity at the lower levels (where the poor people live) is significantly weaker than near the surface (where the rich live) and that there’s a significant Coriolis effect. Unfortunately, the effect depicted is 3 orders-of-magnitude too big.

Pouring a drink on Ceres. Significant Coriolis deflection is apparent.

To explain, six million residents inhabit the interior of the asteroid, which has been spun up to provide an artificial gravity. Ceres has a radius, R C=4.73×10 5R_C = 4.73\times 10^5 m and a surface gravity g C=.27m/s 2g_C=.27\,\text{m}/\text{s}^2. The rotational period is supposed to be 40 minutes (ω∼2.6×10 −3/s\omega\sim 2.6\times 10^{-3}\, /\text{s}). Near the surface, this yields ω 2R C(1−ϵ 2)≡ω 2R C−g C∼0.3\omega^2 R_C(1-\epsilon^2)\equiv \omega^2 R_C -g_C \sim 0.3 g. On the innermost level, R=13R CR=\tfrac{1}{3} R_C, and the effective artificial gravity is only 0.1 g.

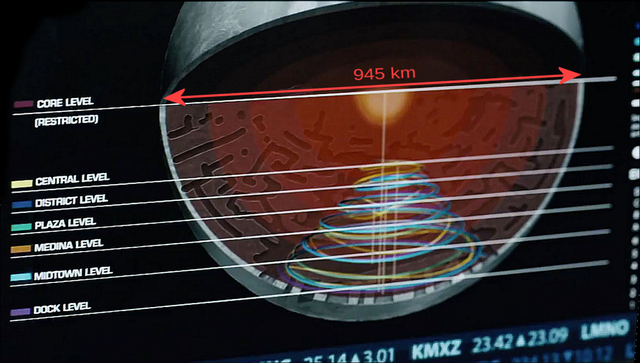
Ceres Station, dug into the interior of the asteroid.

So how big is the Coriolis effect in this scenario?

The equations1 to be solved are

(1)d 2xdt 2 =ω 2(1−ϵ 2)x−2ωdydt d 2ydt 2 =ω 2(1−ϵ 2)(y−R)+2ωdxdt\begin{split} \frac{d^2 x}{d t^2}&= \omega^2(1-\epsilon^2) x - 2 \omega \frac{d y}{d t}\\ \frac{d^2 y}{d t^2}&= \omega^2(1-\epsilon^2) (y-R) + 2 \omega \frac{d x}{d t} \end{split}

with initial conditions x(t)=x˙(t)=y(t)=y˙(t)=0x(t)=\dot{x}(t)=y(t)=\dot{y}(t)=0. The exact solution solution is elementary, but for ωt≪1\omega t\ll 1, i.e. for times much shorter than the rotational period, we can approximate

(2)x(t) =13(1−ϵ 2)R(ωt) 3+O((ωt) 5), y(t) =−12(1−ϵ 2)R(ωt) 2+O((ωt) 4)\begin{split} x(t)&= \frac{1}{3} (1-\epsilon^2) R (\omega t)^3 +O\bigl((\omega t)^5\bigr),\\ y(t)&= - \tfrac{1}{2} (1-\epsilon^2)R(\omega t)^2+O\bigl((\omega t)^4\bigr) \end{split}

From (2), if the whiskey falls a distance h≪Rh\ll R, it undergoes a lateral displacement

(3)Δx=23h(2h(1−ϵ 2)R) 1/2\Delta x = \tfrac{2}{3} h\, {\left(\frac{2h}{(1-\epsilon^2)R}\right)}^{1/2}

For h=16h=16 cm and R=13R CR=\tfrac{1}{3}R_C, this is Δxh=10 −3\frac{\Delta x}{h}= 10^{-3} which is 3 orders of magnitude smaller than depicted in the screenshot above2.

So, while I love the idea of the Coriolis effect appearing — however tangentially — in a TV drama, this really wasn’t the place for it.

1 Here, I’m approximating Ceres to be a sphere of uniform density. That’s not really correct, but since the contribution of Ceres’ intrinsic gravity to (3) is only a 5% effect, the corrections from non-uniform density are negligible.

2 We could complain about other things: like that the slope should be monotonic (very much unlike what’s depicted). But that seems a minor quibble, compared to the effect being a thousand times too large.

Posted by distler at June 14, 2016 4:40 PM

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2889



2 Comments & 0 Trackbacks

Re: Coriolis

I read the books, and I don’t think they make that blunder in them, or at least I didn’t remember spotting it. Actually, I wonder what the biological effects of having a very large Coriolis force would be. If they were large as shown, I doubt the inner ear would be readily able to reach an equilibrium, especially if it was used to a certain levels effects. So transferring between layers would be a messy affair.

Posted by: Haelfix on June 15, 2016 11:18 PM | Permalink | Reply to this

Re: Coriolis

What happened to that other post? Did you delete it? How come?

Posted by: Mitch on June 19, 2016 3:06 PM | Permalink | Reply to this

Post a New Comment