Agent-Based Models (Part 1)
Posted by John Baez
I’m working with Nate Osgood and other folks to develop better modeling tools for epidemiologists. Right now we’re trying to develop a category-based framework for agent-based models. It’s a bit tough since many different techniques are used in such models, without yet an overarching discipline — Nate likened it to the ‘wild West’. I have a lot to learn, but I thought I should start keeping notes on our conversations.
I may or may not post future installments here: I mainly talk about applied category theory on the Azimuth blog. But I thought some of you here might like to know this is going on.
So, what’s the deal with agent-based models?
Agent-based models involve multiple ‘agents’ that have ‘states’ which change over time, often including location in some sort of ‘space’, and which interact via various ‘networks’. Our job is to create convenient, flexible software for creating agent-based models, composing larger ones out of smaller parts, refining existing models, running the models, and viewing them as they run in many different ways.
There is already software for doing these things, such as AnyLogic, NetLogo and Repast). Nate is familiar with it, since his job is building agent-based models. But he’s dissatisfied with it for many reasons. We want to make better software by first analyzing the whole problem with the help of math. All those quoted words—‘agents’, ‘states’, ‘space’, ‘networks’—need to be clarified in a way that’s quite general but also practical.
I’m still learning about all this stuff. Here’s one thing I learned that makes me happy. The internal dynamics of agents—that is, how their states change with time—is often described using two methods:
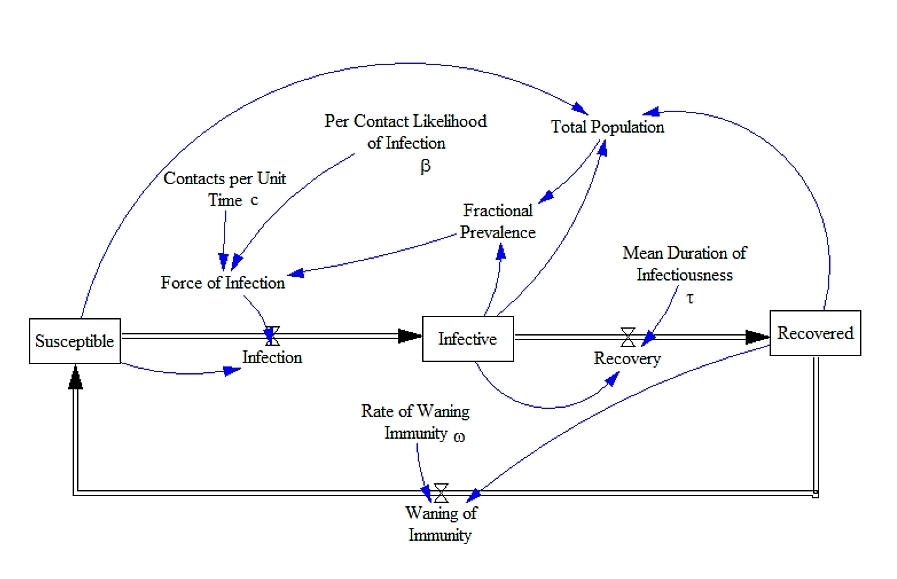
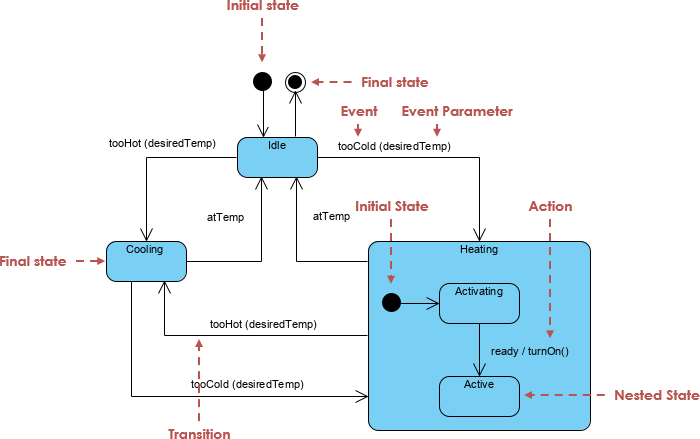
Stock and flow diagrams are good for describing continuous quantities that evolve according to ordinary differential equations, while state diagrams are good for describing discrete quantities that evolve in steps. (In ether case the evolution could be deterministic or stochastic.)
We’ve already worked out the category theory of stock and flow diagrams, and used it to create software for working with such diagrams:
John Baez, Xiaoyan Li, Sophie Libkind, Nathaniel D. Osgood and Eric Redekopp, A categorical framework for modeling with stock and flow diagrams, to appear in Mathematics for Public Health, Springer.
John Baez, Xiaoyan Li, Sophie Libkind, Nathaniel Osgood and Evan Patterson, Compositional modeling with stock and flow diagrams, to appear in Proceedings of Applied Category Theory 2022.
So, it seems we should work out the category theory of state diagrams! Luckily they are similar to stock and flow diagrams, so a lot of the same math should apply: decorated cospans, the operad for undirected wiring diagrams, etc. So, it shouldn’t be a huge task.
However, there are other issues we need to deal with. For example, in a ‘hierarchical state diagrams’ there may be states within a single state. For example in the state ‘infected’ there may be states such as ‘diagnosed’ and ‘undiagnosed’, and in ‘diagnosed’ there may be many states describing whether and how someone has been treated.
Also, there may be variables defined only in a given state, whose dynamics are governed by some stock and flow diagram.
So, we ultimately need a good mechanism for building stock and flow diagrams and state diagrams hierarchically, and mixing the two. Maybe we shouldn’t even treat them as two distinct kinds of diagram, but rather as two ways of using some more general kind of diagram!
I’ll try to take one step at a time. Getting a good category theoretic treatment of state diagrams should be pretty quick.

Re: Agent-Based Models (Part 1)
These state diagrams look very near to digital design of synchronous circuits (having a global state “next step” evolution in discrete time), provided binary data used, both in state and through wires. In computing contexts they often are modeled by Mealy and Moore “machines”. There are some papers by René Guitart in the seventies in the Cahiers and elsewhere dealing with their categorification: “Les machines de Mealy, avec entrées et sorties des categories, mises en parallelè ou en en série, déterminent une bicatégorie MAC qui est aussi bicatégorie de Kleisli de la bimonade D:Cat//_ sur CAT.”
D is the “foncteur diagramme”. As is known, the powerset functor gives the subobjects of a given set and the Kleisli category is that of relations. In Guitart he steps up, so the “diagram functor” sends a small category to the package of all diagrams into it, better said to the corresponding slice category. And he studies the Kleisli category of that, with due care about dimension. Boccali and coauthors revamp this in arXiv:2305.00272 dated this year.