Metric Spaces as Enriched Categories I
Posted by Simon Willerton
Last November I gave a talk entitled “Looking at metric spaces as enriched categories ” at the African Mathematics Seminar at the invitation of Café regular Bruce Bartlett. You may remember that John gave a seminar the month before me.
The talk was aimed at general pure mathematicians, with my main assumption being that the audience knew what a group action, a representation, a metric space and a category were.
My talk was in two halves, the first half was about enriched categories in general and how metric spaces can be viewed as enriched categories. The second half was about ‘applications’ of this that I’d been involved in, that was mainly an overview of the theory of magnitude of metric spaces and a little bit on directed tight spans because of the involvement of some African mathematicians.
I decided that I would write up the first half of the talk and that is what this post and the next post will be on. The definition of enriched category will come in the next post. Hopefully it is clear from the above that these two posts are likely to be rather basic as far as the regulars at the Café are concerned!
Some category theory background
Two general types of categories
As a mathematician you come across categories of various flavours; two general types of categories are the following.
Firstly there are the categories which consist of specific mathematical structures and structure preserving map. Here are some examples:
, vector spaces and linear maps;
, sets and function;
, abelian groups and group homomorphisms;
, topological spaces and continuous maps;
, sets with right -actions and equivariant maps, for a finite groups ;
, representations and intertwining maps for an algebra .
In this post, for concreteness, we will work with vector spaces over the complex numbers, so in particular, an algebra means a complex vector space with an associative unital product; a good example of such an algebra is the group algebra for a finite group .
Secondly, there are the categories that are themselves manifestations of standard mathematical structures. Here are some examples.
When is a finite group there is the one object category with as its set of morphisms and with composition corresponding to multiplication in the group.

Similarly when is an algebra there is the one object category with the underlying set of as its set of morphisms and with composition corresponding to multiplication in .

For a partially ordered set (poset) there is a category (also often called ) whose objects are the elements of and where there is at most one morphism between each pair of objects and a unique morphism precisely when .
- For a topological space there is the poset of open sets in ordered by inclusion, and hence the corresponding category .
Certainly not all categories can necessarily be classified as one of these two types and the two types are very likely not disjoint, but highlighting these two types does give a perspective which can be helpful.
Constructing new categories from old
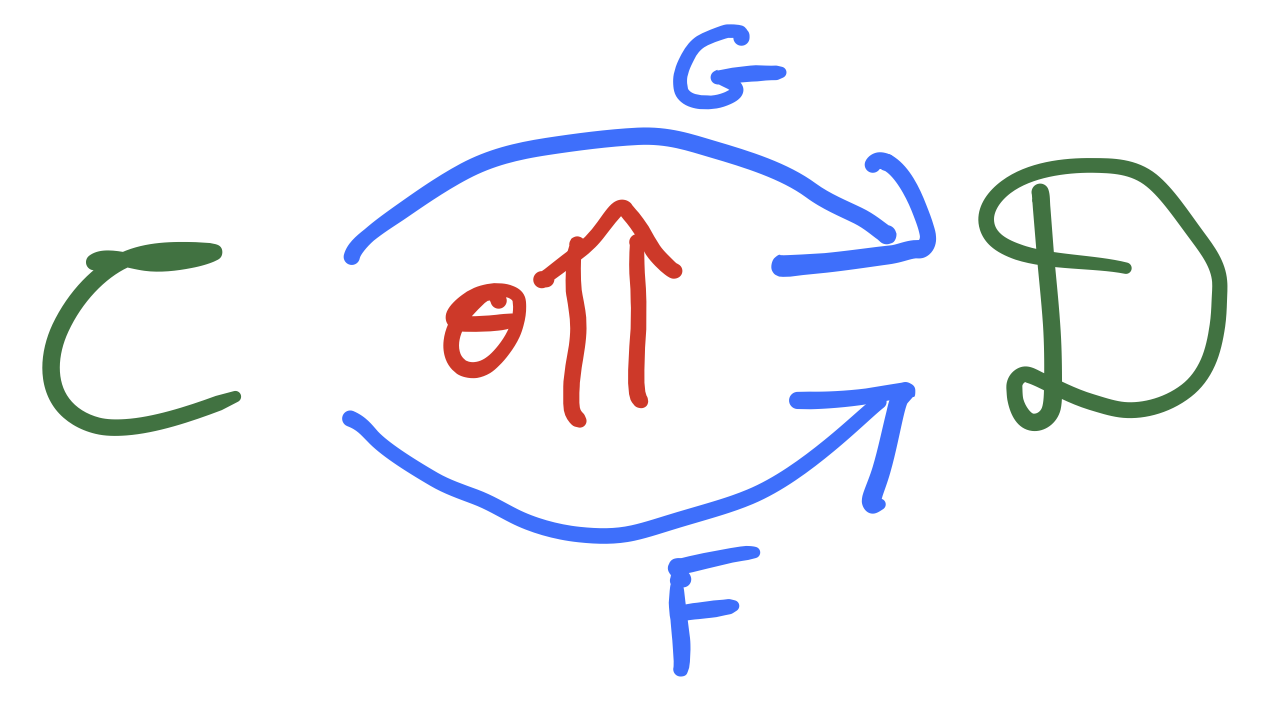
Given categories and you can form the product category where the objects of are pairs with and , and where each hom-set is simply the product of the appropriate hom-sets in and , i.e. . The composition is given in the obvious way: .
You can also define the functor category where the objects are the functors of the form and the morphisms are the natural transformations between such functors.
As usual, denotes the opposite category of , and so the functor category can be thought of as the category of contravariant functors from to .
Scalar-valued functors, or presheaves
For a given category we can take the functor categories and in the special case where and consider the categories
As we will see below, you can consider to be the ‘base category’ or ‘category of scalars’ of ordinary category theory, analogous to a base ring or base field in algebra; so these two categories can be thought of as categories of ‘scalar-valued functors’, analogous to spaces of scalar-valued functions on sets or spaces.
Category theorists will often call the category of presheaves on for reasons given below, and, by extension, will sometimes call the category of co-presheaves on . However, this terminology does seem to obscure, in a slightly intimidating fashion, the fundamental nature of these objects.
Let’s have a look at a couple of examples.
For a finite group and , the associated one-object category, we can obtain the category of of sets equipped with a right -action and the category of of sets equipped with a left -action as functor categories: For instance, if we have a functor then the single object gets sent to a set and the action is given by the functor on the level of hom-sets, .
For a topological space, the category of presheaves is defined to be the contravariant functor category and this is where the category theorists took the term ‘presheaf’ from.
The Yoneda embedding
The Yoneda Lemma is one of the most fundamental results in category theory and a corollary of it is that the functor, the Yoneda embedding, from a category into its category of contravariant functors,
is bijective on the level of hom-sets, i.e., it is a fully faithful embedding.
Similarly, the contravariant version to the other category of functors is also fully faithful:
One analogy that it might be useful to bear in mind is the embedding of a discrete set into its ring of functions via the ‘delta-function’:
where could be any ring such as or , acting as the base ring.
If we consider the Yoneda embedding when we take where is a finite group, then we should have a fully faithful embedding
By definition has a single object with . You can check that is , that is equipped with the left-regular -action. Then should act on the left-regular action by intertwining maps; this it does via the right regular action! The Yoneda embedding being fully faithful is then equivalent to having an isomorphism
Alternative base categories
An important observation at this point is that it is not always correct to use as the ‘base category’. For instance, one feels that just as the category of -actions is given by the functor category so the representation category should be given a functor category like , however this does not quite work. You need to consider linear functors, thus taking into account the fact that both and should be thought of as vector spaces rather than just sets. One way to do this is to use the category of vector spaces as our base category and consider both and as categories enriched over and to take to be the -enriched category of enriched functors. We should see what that means!
We’re taking the perspective here that doing enriched category theory means doing category over a different base category, or category of scalars. This ‘enriching category’ needs certain basic structure, and if one insists on further structure then the theory becomes richer. (We’ll see this next time.) Anyway, the basic structure that is required is that of a monoidal category. A monoidal category consists of a category , a ‘monoidal product’ and a ‘monoidal unit’ object , and these satisfy associativity and unit conditions which we needn’t worry about here.
Let’s consider some pertinent examples.
: this is the category of sets with the cartesian product and a chosen one object set as the unit object; this is the usual ‘base category’.
: this is the category of complex vector spaces with the tensor product and the base field as the unit object.
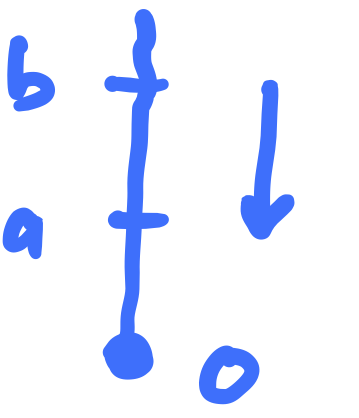
: this is the partially ordered set of non-negative real numbers with infinity added, considered as a category, so there is a single morphism precisely when ; this is equipped with addition as the product, and zero as the unit object. We will denote this monoidal category with .
If you picture the non-negative reals as going upwards then you can imagine the morphisms as allowing you to slide downwards, but not upwards.
Next time we will see the definition of enriched category.

Re: Metric Spaces as Enriched Categories I
I am not seeing how the examples and differ. In particular, where does the latter get its vector space structure from? What am I missing?