Compositional Constructions of Automata
Posted by Emily Riehl
guest post by Ruben van Belle and Miguel Lopez
In this post we will detail a categorical construction of automata following the work of Albasini, Sabadini, and Walters. We first recall the basic definitions of various automata, and then outline the construction of the aformentioned authors as well as generalizations and examples.
A finite deterministic automaton consists of
a finite set (state space),
an initial state and a set of accepting states,
a finite set of input symbols and a transition map for every .
Imagine a frog in pond with a lily pads, which form a by grid. Suppose that the frog sits on a lily pad and can only make jumps of one unit i.e. the frog can jump forwards, backwards, left or right.
Let be the set of lily pads. Let be the lily pad the frog currently is sitting on and let be the lily pad the frog wants to go to. Let be the set of symbols . A jump forward corresponds to an input of and to the map moving the frog forward (if possible) in the grid. Similarly, the symbols and with respective maps and correspond to jumps backwards, left and right, whenever these are possible. The data form a finite deterministic automaton.
The transition maps in the definition of a finite deterministic automaton are morphisms in , the category of finite sets and functions. We can generalize the idea of a finite deterministic automaton, by letting the transition maps be morphisms in more general categories. In particular we will look at Kleisli categories of monads on or .
If the transition map is a map in the Kleisli category of the powerset monad, i.e. functions , we obtain finite non-deterministic automata. In our example that would mean that the frog can choose between a set of different jumps for a given input. If the frog is sitting on lily pad , then is the set of all reachable lily pads that are in front of the frog.
If we let the transition map be a morphism in the Kleisli category of the monad of finitely supported measures on , we obtain weighted automata and if the transition map is a morphism in the Kleisli category of the distribution monad, we obtain Markov automata. In the case of the frog this would mean that the frog prefers some lily pads over others and this preference is given in terms of distributions. If the frog sits on lilypad , then is a distribution on the reachable lily pads in front of the frog.
In the following, we will first consider categories of Markov automata as presented in The compositional construction of Markov process II by Albasini, Sabadini, and Walters and then generalize this to -automata for commutative strong monads on a monoidal category . We will study categories where the morphisms are these generalized automata and look at the monoidal structure and properties this category inherits from and .
Markov Automata
Here, we will consider a definition of automata that deviates from the classical literature. A Markov automaton consists of the following data:
A set of states also denoted .
Two sets of parallel interfaces and (playing the role of inputs/signals)
Two sets of sequential interfaces and together with functions and in (playing the role of start/stop states)
Transition matrices indexed by the parallel interfaces such that for all
Markov automata form a symmetric monoidal category in two distinctly different ways: one in which we compose automata in parallel and one in which we compose in sequence.
Parallel Composition
Let be the category with
objects as finite sets
morphisms as weighted automata whose parallel interfaces are the sets and .
The parallel composite of morphisms is defined to be the weighted automaton with states and whose top and bottom interfaces are the respective set products and with sequential interface functions and . The parallel interfaces are and with transition matrices defined by
where denotes the Kronecker product of matrices. This is shown diagrammatically in the figure below.
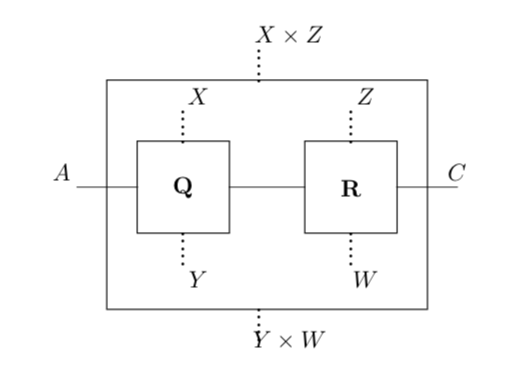
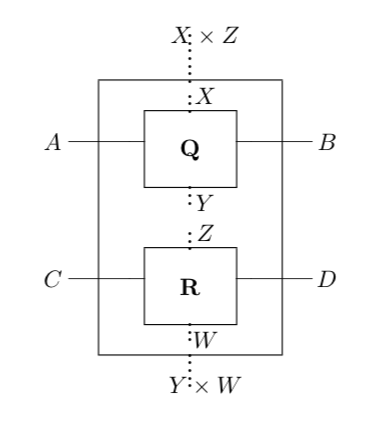
The tensor product of two objects and in is their cartesian product . On morphisms and , the tensor product has as states , transition matrices
and and as sequential interfaces with interface functions and respectively. Note that the identity object is the one element set.
To show is symmetric, we will use the fact that there is a monoidal functor
on the symmetric monoidal category of (finite) sets and relations . This functor acts as the identity on objects and on morphisms by associating to the following automaton:
Each of the sequential interfaces and state space are the singleton set .
The left and right parallel interfaces are and respectively and the transition matrices (in this case numbers) are given by
for and . Symmetry in then follows from being a monoidal functor. Using this technology we will show some nice properties of by pushing them forward through .
Proposition. is compact closed.
This in particular allows us to define the notion of feedback. To show that (and hence ) is compact closed we instead show that each object in is a Frobenius algebra and apply the following lemma.
Lemma. If an object in a monoidal category forms a Frobenius algebra then it is dual to itself.
Let be the diagonal map, thought of as a morphism in and the unique morphism to the terminal object. Moreover given a morphism , let denote the opposite relation (by simply reversing the arrow). Then the monoid structure for the Frobenius algebra of an object in is given by and, dually, the comonoid structure by .
Sequential Composition
Let be the category with
objects as finite sets
morphisms as weighted automata
whose sequential interfaces are the sets and .
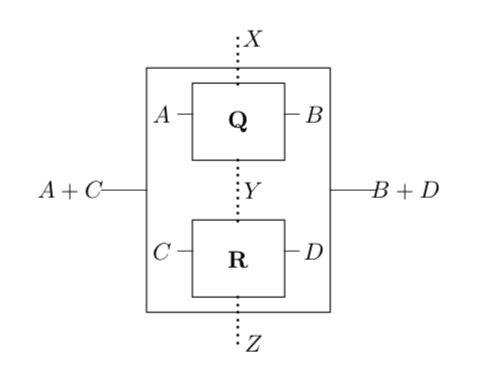
We define the sequential composite of two morphisms and to be the weighted automaton whose states are given by the disjoint union quotiented by the relation . The parallel interfaces are and and top and bottom interfaces are and with the respective interface functions
If we let and and denote the equivalence class of state in , then the transition matrices are given by
where all other entries are zero. This is shown diagrammatically below.
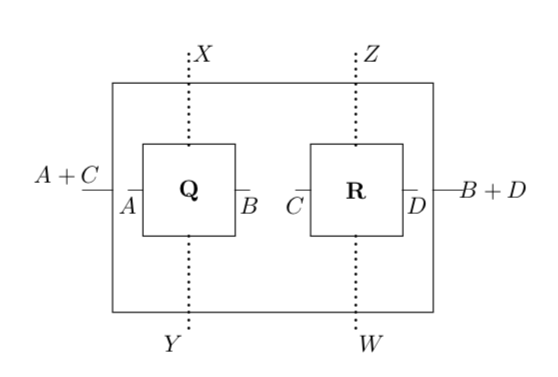
The tensor product of and has states without any quotienting. The parallel interfaces are again and while top and bottom interfaces and have interface functions and . The transition matrices are given by where all other entries are again zero.
Just as in the case of , one can show is a compact closed symmetric monoidal category by defining a monoidal functor .
-Automata
We now generalize the preceding categories to work with a commutative strong monad. Let be a (strict) symmetric monoidal category and let be a commutative monad on with strength . Let be the Kleisli category of this monad. The strength induces a monoidal structure on (see Folklore: Monoidal kleisli categories). We will denote the tensor product and unit object on also by and .
Definition. A -automaton consists of
an object in ,
morphisms and in (sequential interfaces) and
objects and in (parallel interfaces) together with a map in (transition morphisms).
Parallel composition
Consider two -automata and .
The parallel composite of and is given by the -automaton where is used to mean composition in .
Let be the category that has the same objects as and where a morphism from to is a -automaton whose parallel interfaces are given by and and where composition is given by parallel composition.
Given two -automata and , we can form a new -automaton which we call the parallel tensor product. The parrallel tensor product together with the object define a monoidal structure on .
We will now define a (strict) monoidal functor The functor acts as the identity on objects and sends a morphism in to the -automaton
Because the monoidal structure on is symmetric, so is the monoidal structure on using the monoidal functor .
Note that sends Frobenius algebras to Frobenius algebras and is surjective on objects.
Proposition. If is compact closed, so is
Remark. We have tried to also generalize the sequential operations to -automata, but we will leave the details of this construction for future work.
Examples
Consider the following game in a casino: the player is asked to place a bet, let’s say the player decides to place a bet of £. After the bet is placed, the dealer blindly picks a coin from a bag of (fair and unfair) coins; suppose the dealer picks coin , which has probability on heads. Then the dealer flips the coin. If coin lands on heads, the player wins £. If it falls on tails, the player loses the placed bet of £.
We represent the bank balance of the player by . We furthermore suppose that the player enters the casino with £ and has decided to leave the casino when their bank balance reaches states in .
If we let to be the set of possible bets, i.e. and let be the bag of coins the dealer picks from. For a coin , we denote the probability on heads by . For a bet and a bank balance of such that , let be the measure on defined by This measures the chance of moving from a bank balance of to a balance of when playing the game.
For a bet and a bank balance of such that , let be the measure on defined by
as the player is not allowed to bet more money than they have.
This defines the Kleisli map and the data form a weighted automaton. Note that is a so called deadlock state, since the player’s bank balance won’t change anymore after reaching . In particular, if is not an element of , the player will have to keep playing the game forever.
Suppose now that the casino has multiple tables with different bags of coins and suppose that two friends go to the casino together. Then parallel compositions combines the information of the two friends playing at the same table, i.e. the game is played with the same coin. The parallel product and the sequential sum both combine the information of the two friends playing at different tables. The product measures the chance that person 1 reaches state and that person 2 reaches state , while the sum measures the chance that that person 1 reaches state or that person 2 reaches state .
If the player starts with £ and decides to move to a different table when reaching £ and to stop playing when their bank balance is £, we can model the combination of the two games with the sequential composition.

Re: Compositional Constructions of Automata
Diagram links don’t work
Appending .png to them brings up a page with the picture.