Hardy, Ramanujan and Taxi No. 1729
Posted by John Baez
In his book Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, G. H. Hardy tells this famous story:
He could remember the idiosyncracies of numbers in an almost uncanny way. It was Littlewood who said every positive integer was one of Ramanujan’s personal friends. I remember once going to see him when he was lying ill at Putney. I had ridden in taxi-cab No. 1729, and remarked that the number seemed to be rather a dull one, and that I hoped it was not an unfavourable omen. “No,” he replied, “it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.”
Namely,
But there’s more to this story than meets the eye.
First, it’s funny how this story becomes more dramatic with each retelling. In the foreword to Hardy’s book A Mathematician’s Apology, his friend C. P. Snow tells it thus:
Hardy used to visit him, as he lay dying in hospital at Putney. It was on one of those visits that there happened the incident of the taxicab number. Hardy had gone out to Putney by taxi, as usual his chosen method of conveyance. He went into the room where Ramanujan was lying. Hardy, always inept about introducing a conversation, said, probably without a greeting, and certainly as his first remark: “I thought the number of my taxicab was 1729. It seemed to me rather a dull number.” To which Ramanujan replied: “No, Hardy! No, Hardy! It is a very interesting number. It is the smallest number expressible as the sum of two cubes in two different ways.”
Here Hardy becomes “inept” and makes his comment “probably without a greeting, and certainly as his first remark”. Perhaps the ribbing of a friend who knew Hardy’s ways?
I think I’ve seen later versions where Hardy “burst into the room”.
But it’s common for legends to be embroidered with the passage of time. Here’s something more interesting. In Ono and Trebat-Leder’s paper The 1729 K3 surface, they write:
While this anecdote might give one the impression that Ramanujan came up with this amazing property of 1729 on the spot, he actually had written it down before even coming to England.
In fact they point out that Ramanujan wrote it down more than once!
Before he went to England, Ramanujan posed a lot of puzzles in the questions section of the Journal of the Indian Mathematical Society. In 1913, in Question 441, he challenged the reader to prove a formula expressing a specific sort of perfect cube as a sum of three perfect cubes. If you keep simplifying this formula to see why it works, you eventually get
In Ramanujan’s Notebooks, Part III, Bruce Berndt explains that Ramanujan developed a method for finding solutions of the diophantine equation in item 20(iii) of his “second notebook”. This is one of three notebooks he left behind after his death, and the results in this one were written down before Ramanujan first went to England. Here Ramanujan lists many example solutions, the simplest being
In 1915 Ramanujan posed another puzzle about writing a sixth power as a sum of three cubes, Question 661. And he posed a puzzle about writing as a sum of three cubes, Question 681.
Finally, much later Ramanujan revisited the diophantine equation in his so-called Lost Notebook. This was actually a pile of loose unnumbered pages written by Ramanujan. George Andrews found them in a box in Trinity College, Cambridge in 1976.
Now the pages have been numbered, published and studied. Here is page 341 of Ramanujan’s Lost Notebook where he came up with a method for finding an infinite family of solutions to Euler’s diophantine equation :
As you can see, one example is
In Section 8.5 of George Andrews and Bruce Berndt’s book Ramanujan’s Lost Notebook: Part IV, they discuss Ramanujan’s method here, calling it “truly remarkable”.
In short, Ramanujan was well aware of the special properties of the number 1729 before Hardy mentioned it. And something prompted Ramanujan to study the equation again near the end of his life, and find a new way to solve it.
Could it have been the taxicab incident??? Or did Hardy talk about the taxi after Ramanujan had just thought about the number 1729 yet again? In the latter case, it’s hardly a surprise that Ramanujan remembered it.
Thinking about this story, I’ve started wondering about what really happened here. First of all, as James Dolan pointed out to me, you don’t need to be a genius to notice that
Was Hardy, the great number theorist, so blind to the properties of numbers that he didn’t notice either of these ways of writing 1729 as a sum of two cubes? Base ten makes it very easy to spot if you know your cubes, and I’m sure Hardy knew and .
Second of all, how often do number theorists come out and say a number is uninteresting? Except in that joke about the “least uninteresting number”, I don’t think I’ve heard it happen.
My wife Lisa suggested an interesting possibility that would resolve these puzzles:
Hardy either knew of Ramanujan’s work on this problem, or noticed himself that 1729 could be written as a sum of perfect cubes in two ways. He wanted to cheer up his dear friend Ramanujan, who was lying deathly ill in the hospital. So he played the fool by walking in and saying that 1729 was “rather dull”.
I have no real evidence for this, but I like how it flips the meaning of the story. And it’s not impossible. Hardy was, after all, a bit of a prankster: each time he sailed across the Atlantic he sent out a postcard saying he had proved the Riemann Hypothesis, just in case he drowned.
We could try to see if there really was a London taxi with number 1729 at that time. It would be delicious to discover that it was merely an invention of Hardy’s. But I don’t know if records of London taxi-cab numbers from around 1919 still exist.

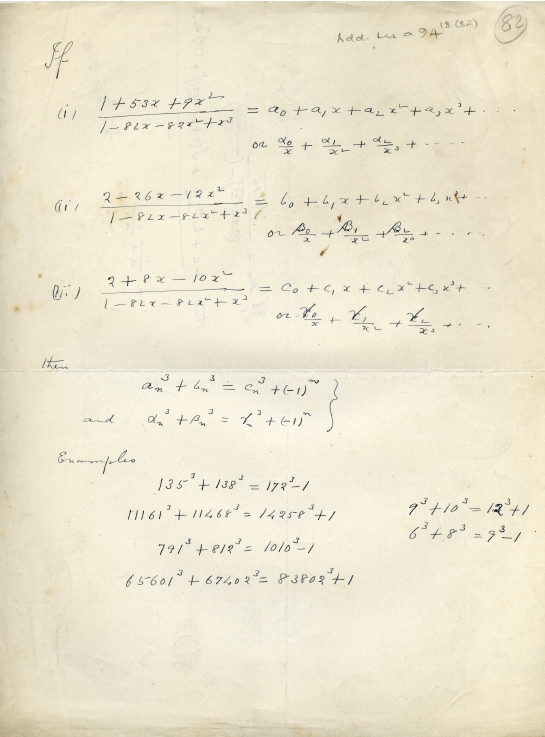

Re: Hardy, Ramanujan and Taxi No. 1729
Do we know whether Hardy’s taxi was motorized or horse-drawn? Your post implies that the famous incident happened in 1919, and Wikipedia says:
Probabilities aside, maybe Hardy’s word taxi-cab tells us it was motorized. In British English at least, no one says “taxicab” any more; it sounds nearly as antiquated to my ears as “omnibus”. But I don’t know how the terminology evolved in the early days of motorization.
Sherlock Holmes was always jumping into hireable horse-drawn transport as he hurried off to catch evil-doers. My memory of the stories is that the word used was “carriage”, never “taxicab”. But I’m too lazy to go and check. Sherlock was doing his thing only a couple of decades before the 1729 incident.
(In case you’re wondering why I’m asking, I started trying to find out whether there could plausibly have been a taxi number 1729 in 1919, and quickly ran into this question.)