The Riemann Hypothesis (Part 1)
Posted by John Baez
I’ve been trying to understand the Riemann Hypothesis a bit better. Don’t worry, I’m not trying to prove it — that’s a dangerous quest. Indeed Ricardo Pérez-Marco has a whole list of things not to do if you want to prove the Riemann Hypothesis, such as:
Don’t expect that the problem consists in resolving a single hard difficulty. In this kind of hard problem many enemies are on your way, well hidden, and waiting for you.
and
Don’t go for it unless you have succeeded in other serious problems. “Serious problems” means problems that have been open and well known for years. If you think that the Riemann Hypothesis will be your first major strike, you probably deserve failure.
Taken together, his pieces of advice are sufficiently discouraging that he almost could have just said “don’t try to prove the Riemann Hypothesis”.
But trying to understand what it means, and how people have proved vaguely similar conjectures — that seems like a more reasonable hobby.
In what follows I want to keep things as simple as possible, because I’m finding, as I study this stuff, that people are generally too eager to dive into technical details before sketching out ideas in a rough way. But I will skip over a lot of standard introductory stuff on the Riemann zeta function, since that’s easy to find.
Of course the Riemann Hypothesis says that the Riemann zeta function has zeros only at negative even integers (the ‘trivial zeros’) and on the line (the ‘nontrivial zeros’). The function looks simple enough that it’s surprising nobody has settled this. But still, the skeptic might ask: is solving this really worth a million dollars? Is this problem famous just because it’s hard?
If you dig a bit deeper you’ll see that the Riemann Hypothesis implies or is equivalent to a lot of nice statements in number theory. These reveal a bit more about why it matters. I’d summarize them all by saying that prime numbers are distributed as nicely as they could be. For example, if the number of primes is , the Prime Number Theorem says that a pretty good approximation to is
More precisely, it says
But the Riemann Hypothesis says more about how good this approximation is! The Riemann Hypothesis is equivalent to
for some for all .
I bet someone has given a heuristic argument for this by assuming the primes are ‘randomly distributed’ in some reasonable way. If so, the Riemann Hypothesis says there aren’t ‘unreasonably large fluctuations’ in the distribution of primes.
One can sharpen this idea to a crazy level of precision: in 1976 Schoenfeld showed the Riemann Hypothesis is equivalent to
That’s impressive. But I don’t think this particular statement, including the number 2657, gets us much closer to the deep inner meaning of the Riemann Hypothesis.
If you dig into how the zeros of the zeta function are connected to the distribution of primes, you soon meet Riemann’s explicit formula. This is a formula for as a sum over zeros of the zeta function. The trivial zeros give a simple approximation to , while the nontrivial zeros contribute a bunch of corrections. Each of these corrections is an ever-growing wave-like function, whose frequency and rate of growth depends on the location of that zero!
So, we could say the prime numbers and the nontrivial zeros of the Riemann zeta function give the ‘particle’ and ‘wave’ pictures of the same phenomenon… where I’m alluding to ideas from quantum mechanics, and the Fourier transform. This analogy seems to be fairly deep, and maybe I’ll say more about it sometime.
More poetically, we could say the Riemann zeta zeros reveal the ‘music of the primes’. That’s one of the guiding metaphors of this book:
- Barry Mazur and William Stein, Prime Numbers and the Riemann Hypothesis, Cambridge U. Press, Cambridge, 2016.
and I really recommend this book if you want to get a feeling for Riemann’s explicit formula without sinking into technicalities.
Before I show you Riemann’s explicit formula, let me show you a movie of how it works:
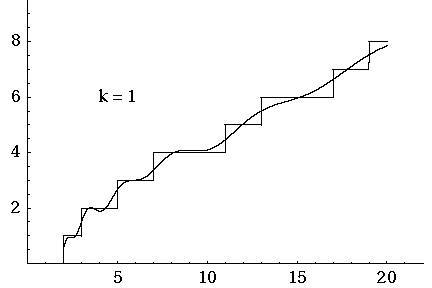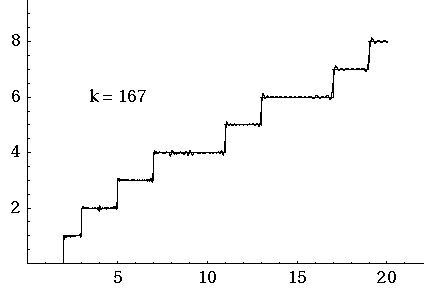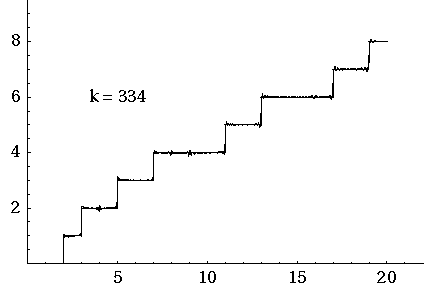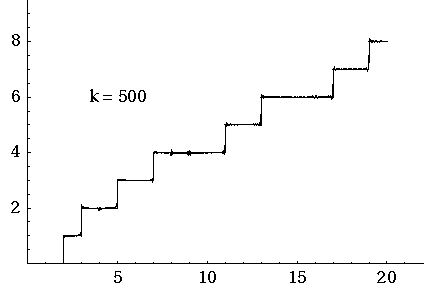
Here J. Laurie Snell, Bill Peterson, Jeanne Albert and Charles Grinstead show what happens when you start with the simple approximation to and then add up the waves coming from the first 500 nontrivial zeros of the Riemann zeta function.
That movie is really fun. I must have watched it dozens of times by now. And if you look carefully you’ll see some interesting things.
First, you can see a version of the Gibbs phenomenon: the strong oscillations near the primes, where takes a step up. But this is something you should always expect when trying to approximate a step function with a sum of smooth waves.
More subtly, there are little ‘glitches’ at the prime powers. Why is that? Well, it’s because Riemann’s explicit formula starts out life as a formula not for but another function . This counts not only all primes but all prime powers , but in a funny way: it counts a prime power as worth . So, for example, since there are 3 primes less than 6, but also the prime power .
From Riemann’s explicit formula for you can work out one for . But the prime powers still maintain a ghostly presence as ‘glitches’, which only go away in the limit where you add up all the waves.
What are these waves, exactly? It’s easiest to give the formula for . Here’s the formula:
where are the nontrivial zeros of the Riemann zeta function. The scary integral is due to the trivial zeros of the zeta function, but let’s ignore that! I only want you to look at the sum over the nontrivial zeros.
The function makes everything more complicated, so just think about . If we assume the Riemann Hypothesis, the real part of is always , so
with real, so
In short, this function grows like but also oscillates at a rate depending on . (You may wonder how gets to be real, but that’s because the nontrivial zeros come in complex conjugate pairs.)
So, if the Riemann Hypothesis is true, we know these correction terms grow at a known rate, and that helps experts get good estimates on and then the prime counting function . But if the Riemann Hypothesis is false, all this gets ruined. There will then be zeros with real part greater than 1/2, and these will give correction terms that grow faster.
That last paragraph was extremely superficial, mainly because of my ignorance. But there’s a reason for my ignorance: when I reached this point, I decided that this direction was not the most interesting.
What I really wanted to know is why the Riemann Hypothesis should be true. I figured that to get some sense of this, I should look at the Weil Conjectures, which are a kind of baby version of the Riemann Hypothesis. Unlike the Riemann Hypothesis, these conjectures have actually been proved. So we have some idea why they’re true!
Like the Riemann Hypothesis, these conjectures describe ‘wave-like corrections’ to a simple formula for counting something: not primes, but points on an algebraic variety over a finite field. Again, there’s one such correction for each zero (or pole) of some kind of zeta function. But in this case there’s an actual explanation for the location of the zeta function zeros! So there’s a good reason that they lie where they do. And it turns out to be quite mind-blowing.
That’s what I really wanted to talk about today. But I see that my preparatory throat-clearing has gone on so long that at least one more blog post will be required.
In the meantime, you can watch another video of how the prime counting function gets approximated by waves coming from the nontrivial zeta zeros:
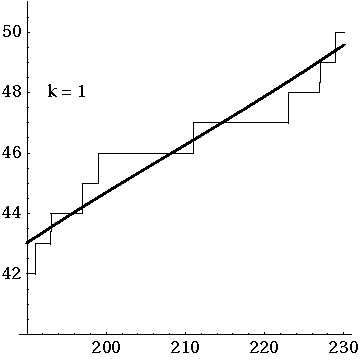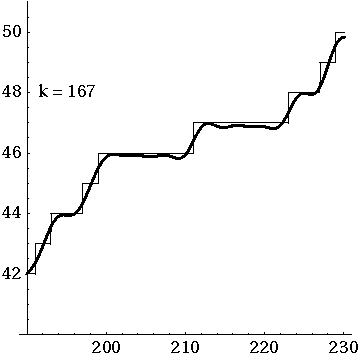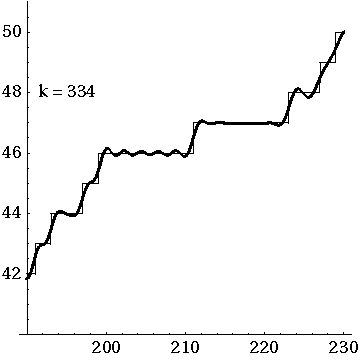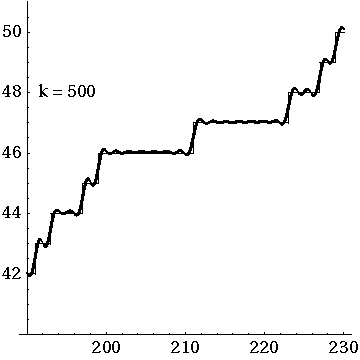
It’s interesting to me how the whole curve sways up and down. I’m not sure what causes that.

Re: The Riemann Hypothesis (Part 1)
Have you seen this blog post by Scott Aaronson?
We discussed his work on the Busy Beaver problem somewhere and this Turing Machine design was a bonus from that work.
Apart from the techniques for Optimising turing machine design it uses the fact that it is possible to state the Riemann Hypothesis very simply (low on the arithmetical hierarchy).