The Riemann Hypothesis (Part 3)
Posted by John Baez
Now I’ll say a little about the Weil Conjectures and Grothendieck’s theory of ‘motives’. I will continue trying to avoid all the technical details, to convey some general flavor of the subject without assuming much knowledge of algebraic geometry.
I will start using terms like ‘variety’, but not much more. If you don’t know what that means, imagine it’s a shape described by a bunch of polynomial equations… with some points at infinity tacked on if it’s a ‘projective variety’. Also, you should know that a ‘curve’ is a 1-dimensional variety, but if we’re using the complex numbers it’ll look 2-dimensional to ordinary mortal’s eyes, like this:

This guy is an example of a ‘curve of genus 2’.
Okay, maybe now you know enough algebraic geometry for this post.
Last time I explained Hasse’s theorem saying how to count points on elliptic curves over finite fields: the number of points is a pretty obvious guess plus two ‘correction terms’ that grow and oscillate as the number of elements in your finite field increases. The obvious guess grows like , the number of elements in your field together with a point at infinity. The correction terms grow like — and that fact is a baby version of the Riemann Hypothesis!
To be precise: for any elliptic curve defined over the integers, its number of -points where is
where .
The brilliant algebraic geometer André Weil knew about this, and he guessed how it should generalize to other kinds of curves. He announced his generalization seven months after Germany invaded Poland, starting World War II. At the time, he was confined to a French military prison for failing to report for duty — he was a pacifist.
He announced his result before he’d fully proved it. He just had an outline of a proof. Later he wrote:
In other circumstances, publication would have seemed very premature. But in April 1940, who could be sure of a tomorrow? It seemed to me that my ideas contained enough substance to merit not being in danger of being lost.
How could you guess this generalization? If we work over the field , an elliptic curve looks like an ordinary torus: the surface of a 1-holed doughnut. Other curves, look like the surfaces of doughnuts with other numbers of holes. We call the number of holes the ‘genus’ of the curve.
There’s only one kind of curve with genus 0, namely the projective line, and its number of points is
since we can chop it into two pieces: the ordinary line and a point at infinity.
Based on this extremely limited data, if I had to guess the number of -points of a curve of genus , I would guess
And that’s what Weil guessed, and eventually proved!
Weil’s Theorem. Given a smooth algebraic curve of genus defined over , its number of -points where is
where all the have .
So, instead of just two ‘correction terms’, there are of them.
It took a lot of work for Weil to prove his theorem: even after getting the basic strategy, he had to redo the foundations of algebraic geometry, generalizing a lot of stuff from the complex numbers to finite fields. As he later wrote:
I could see that, to ensure the validity of the Italian methods in characteristic , all the foundations would have to be redone, but the work of van der Waerden, together with that of the topologists, allowed me to believe that it would not be beyond my strength.
I don’t want to talk about his proof yet. For that I highly recommend this paper, which is where I’m borrowing the quotes from:
- James Milne, The Riemann Hypothesis over Finite Fields: from Weil to the present day, in The Legacy of Bernhard Riemann after One Hundred and Fifty Years, eds. Lizhen Ji, Frans Oort, Shing-Tung Yau, ALM 35, 2015, pp. 487–565.
Instead, today I just want to give a rough intuitive idea of what’s going on. This will be vague, verging on mystical. I can come back later and firm it up.
I’ll illustrate what I want to say with an elliptic curve, but the same idea works for a curve of any genus.
An elliptic curve over can always be gotten by taking a parallelogram in the complex plane and identifying opposite edges. For simplicity let’s consider a square. When we identify its opposite edges, the resulting torus is the disjoint union of a point, two open intervals, and an open square:
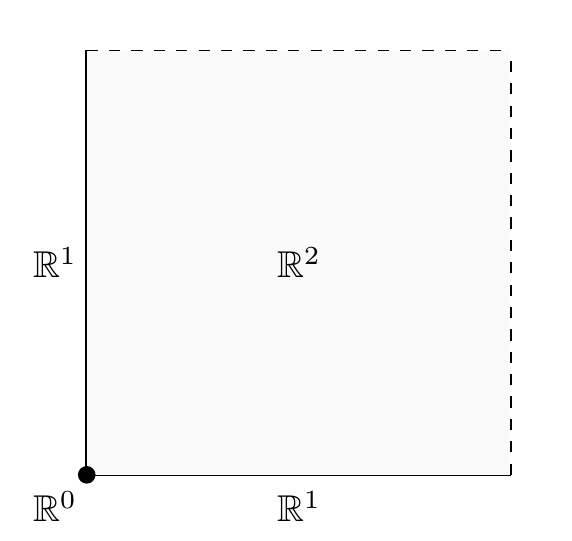
So, if we were trying to count the points in the torus — a futile quest, since there are uncountably many — we might guess the answer is
and with luck this might equal
Now there actually is a reasonable choice of the value for . Namely, -1. That may seem very weird, but it’s the right choice in Schanuel’s approach to Euler characteristic. In particular, this choice gives
which is the correct Euler characteristic of the torus. In general if you take a nice enough compact space and chop it into disjoint ‘open cells’ that are copies of , this method gives the Euler characteristic. You can find lots more details here:
• John Baez, The mysteries of counting: Euler characteristic and homotopy cardinality.
Now, that may seem weird enough, but another weird thing is that we’re doing complex algebraic geometry, so you might think the real numbers shouldn’t be in the story at all! But somehow they are lurking there. For example, algebraic geometers call an elliptic curve over the complex numbers a curve, because it’s 1-dimensional as a complex variety, but they still like to use its cohomology groups:
which admit that topologically it’s a 2-dimensional thing that can be built out of a 2-dimensional cell, two 1-dimensional cells and one 0-dimensional cell.
Of course everyone in algebraic geometry is used to this. But to emphasize the weirdness, we could draw our elliptic curve like this:
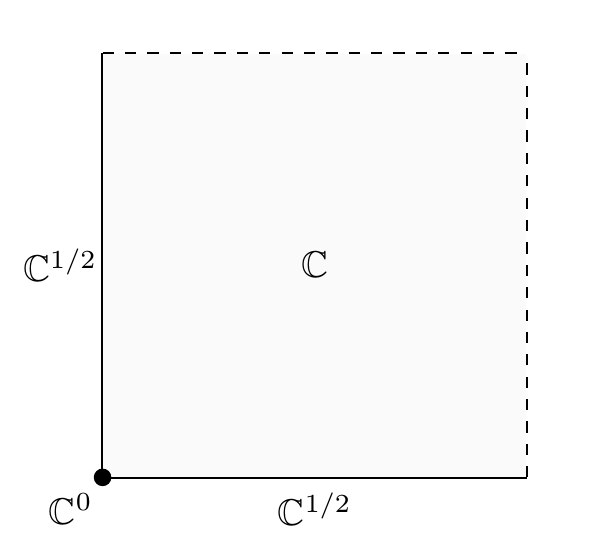
showing that appears as the ‘square root’ of .
The reason I’m making such a big deal out of this is that Weil’s job was to figure out how all this works with replacing . There’s really no field that deserves to be called , in general (although you could argue there is when is a quadratic extension of some other field). But we could still try to guess the number of points in an elliptic curve over based on these wacky ideas, like this:
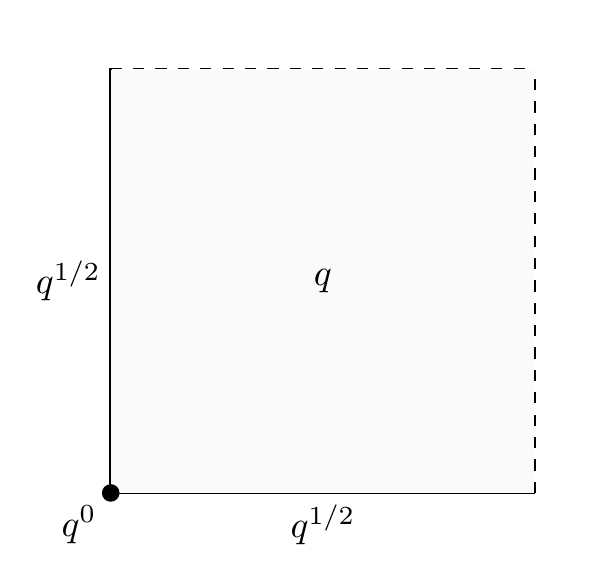
This suggests the answer
or if ,
But this is wrong.
It’s not surprising that this stupid guess is wrong; what’s surprising is that it’s not completely off the mark! The right answer is
for some with .
So, we have some numbers and saying that the 1-dimensional pieces of our elliptic curve have more ‘personality’ than the stupid guess predicts. These numbers have the same absolute value as the stupid guess predicts, but they also have a complex phase depending on our curve.
We also have some minus signs that aren’t in the stupid guess, familiar from Schanuel’s theory of Euler characteristic. Somehow the 1-dimensional pieces of our curve don’t add points, they subtract them!
All this may sound too wacky to be worth thinking about, but in fact some ideas like this turn out to work not just for curves, but also for higher-dimensional algebraic varieties. That’s what the full-fledged Weil Conjectures say!
Namely, suppose we have a smooth -dimensional projective algebraic variety defined by polynomials with integer coefficients, and we want to count its points over , where . Then we can chop it into very abstract ‘pieces’ of ‘homological dimension’ . Note the dimension doubling here: for example, when we have a curve, but this has a piece of homological dimension two, as shown in the pictures above.
In general, each piece of having homological dimension will contribute
to the number of points, where and the sign depends on whether is even or odd. To get the total number of points of , we just add up these contributions.
In particular, there will be one piece of the top dimension, and I’m pretty sure this always contributes to the number of points. Then there are oscillating ‘correction terms’ that grow like and so on, coming from the lower-dimensional pieces.
These ‘pieces’ usually aren’t so vividly geometrical as I’ve tried to made them seem in the elliptic curve example. To get your hands on them you need to use cohomology theory. Grothendieck became obsessed with trying to understand them, and he called them ‘motives’. They’re quite amazing entities, since as we’ve seen they have dimensions that are half-integer multiples of the usual dimensions that varieties can have, and their ‘number of points’ can be a complex number — although when put together to form a variety, these complex numbers always add up to give a natural number. They remind me a bit of quantum mechanics, where you often compute real-valued observable quantities as a sum of complex numbers, and we have lots of oscillating ‘phases’. This analogy could be fleshed out in quite a bit more detail.
Grothendieck never fully succeeded in clarifying his thoughts on motives, and much remains mysterious about them — though also a lot is known. In particular, he never finished proving the Weil Conjectures using his line of thinking! He proved a lot, but he never showed these complex numbers have the absolute values that the Weil Conjectures predict. So he never really worked out the growth rates of these ‘correction terms’ I keep talking about. He reduced this problem to what are now called the ‘Standard Conjectures’. These can be seen as conjectures about motives. They are absolutely fundamental to algebraic geometry. But nobody has ever managed to prove them! Deligne finished proving the Weil Conjectures in a different way.
I would like to say more about all this someday. But for now let’s just take stock of where we are. I started talking about the Riemann Hypothesis, but then I switched to a simpler version, the Weil Conjectures. In both the problem is understanding the oscillating ‘correction terms’ to a naive way of counting something. I sketched how in the Weil Conjectures, where we are trying to count points on a variety, these correction terms come from lower-dimensional ‘pieces’ of the variety, called motives. So, we can hope that in the Riemann Hypothesis something similar is going on.
But I have not said anything about how the Riemann Hypothesis is connected to the Weil Conjectures. What sort of ‘points’ on what sort of thing are we trying to count in the Riemann Hypothesis? How might we chop this thing up into generalized ‘motives’ of some sort? There’s a lot known about this, but much more remains unknown. We can hope, though, that this thing — whatever it is — is some sort of space such that integers act like functions on this space. We can also hope that this thing is some sort of generalized ‘curve’, built from a piece of homological dimension 2, a piece of homological dimension 0, and infinitely many pieces of homological dimension 1, which correspond to the nontrivial zeros of the Riemann zeta function. The fact that these pieces have homological dimension 1 should explain why these zeros have real part 1/2.
I also have not said anything about how Weil proved the Weil Conjectures for curves, or how Grothendieck almost proved them for higher-dimensional algebraic varieties. As I mentioned, Weil had to redo the foundations of algebraic geometry to handle the case of curves — and Grothendieck had to redo them over again, in a deeper way, to handle the more general case. People trying to prove the Riemann Hypothesis by continuing the same strategy feel the need to redo the foundations yet again, and that’s where things get really exciting.
Indeed, the more I learn about this, the more in awe I am of how much mathematics has arisen, directly or indirectly, from the Riemann Hypothesis — and how much more could still come out of it.


Re: The Riemann Hypothesis (Part 3)
Perhaps this is a good occasion to mention Weil’s letter from his prison cell to his philosopher sister, Simone, translated here, which invokes an analogy reused by John here:
Serge Lang was somewhat critical in his response to the publication of this translation.