K3 Surfaces and the Number 24
Posted by John Baez
I’m seeking an explicit vector field with exactly 24 zeros, each of index 1, on a K3 surface. This sounds sort of dry and boring, but it’s not! Let me explain.
This post will start out with some gentle exposition, and then lead to an open question that’s been bothering me. If you’re a beginner, start at the beginning. If you’re an expert, maybe start at the end.

André Weil named ‘K3 surfaces’ after the mathematicians Kummer, Kähler and Kodaira, but also after the second highest mountain in the world, K2.
This makes them sound remote and forbidding. But let’s climb up to the base camp and get a good view. Then, I’ll ask your help for finding a specific vector field on a specific K3 surface, that may help us see very vividly why the third stable homotopy group of spheres is .
K3 surfaces are a certain class of smooth 2-dimensional complex varieties, hence the name ‘surfaces’. But they’re 4-dimensional when viewed as real manifolds. They’re all the same as real manifolds, i.e. diffeomorphic — but they’re not all the same as complex varieties!
The simplest K3 surface, the ‘Fermat quartic surface’, comes from taking the space of nonzero complex solutions of
and ‘projectivizing’ it: counting two solutions as the same if they differ by nonzero factor , like and .
The Fermat quartic surface lies inside the projective space . In fact any smooth quartic surface in is a K3 surface, so now you have tons of examples.
But what is a K3 surface? I’ll explain it mainly using complex differential geometry, not algebraic geometry: I’m just that kind of guy.
A K3 surface is a simply connected Calabi–Yau manifold of complex dimension 2.
The only other Calabi–Yau manifolds of this dimension are diffeomorphic to a 4-torus , so the phrase ‘simply connected’ is designed to rule out these others, which have a very different flavor.
But what’s a Calabi–Yau manifold? Let me pick one of several equivalent definitions.
A Calabi–Yau manifold is an -dimensional compact complex manifold for which there exists a nowhere vanishing holomorphic -form.
Remember, an -dimensional complex manifold is a manifold where we can locally choose complex coordinates , with holomorphic transition functions between different coordinate charts. A holomorphic -form then looks like
where is a holomorphic function, depending on the chart.
Here’s a fancier way of saying the same thing. Holomorphic -forms on an -dimensional complex manifold are sections of a holomorphic line bundle called the canonical bundle. The existence of a nowhere vanishing holomorphic -form just says this bundle is trivial. So a Calabi–Yau manifold is a compact complex manifold with trivial canonical bundle.
Putting it all together, a K3 surface is a 2d compact complex manifold that’s
- Calabi–Yau (its canonical bundle is trivial)
and
- simply connected (to rule out tori).
Amazingly, from these bare assumptions people can completely work out the topology of any K3 surface, and ultimately show they are all diffeomorphic!
That takes a lot of work. It’s easier to show their Euler characteristic must be exactly 24. There’s a nice proof in Proposition 1.2.12 here:
- Svetlana Makarov, General introduction to K3 surfaces.
I like this because the number 24, my favorite number, comes straight out of the number 12 sitting in the gadget called the ‘Todd class’, defined using the function
There’s a lot more to say about this, but let’s move on.
Another amazing thing about K3 surfaces is that they’re all hyper-Kähler manifolds. Without getting into the full definition, this implies that besides the usual complex structure on the tangent bundle, which lets us multiply tangent vectors by , and there are two others, which we’ll call multiplying by and , that obey the usual quaternion relations:
Given these two amazing facts we can do something cool. First, the Poincaré–Hopf theorem implies that if a compact manifold has Euler characteristic and you have a smooth vector field on it with only isolated zeros of index , it must have exactly of them. Here an ‘isolated zero of index ’ is a point where in some local coordinates the vector field looks either like this:
or this:
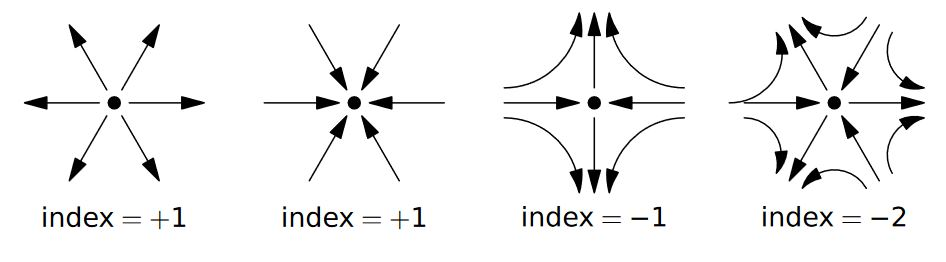
So if a K3 surface has a vector field with only isolated zeros of index , it must have exactly 24 of them. Less obviously, any K3 surface does have such a vector field!
What I want, though, is an explicit example! David Roberts asked for such an example, but the replies only gave an existence proof:
- David Roberts, Vector field on a K3 surface with 24 zeros, MathOverflow.
Why do we care? Here’s why. Take a K3 surface with a vector field on it with 24 isolated zeros of index . Remove small open balls around these zeros. The remaining manifold with boundary, say , is a cobordism from the disjoint union of 24 copies of to the empty set. Furthermore it is a ‘framed’ cobordism, because its tangent bundle has a trivialization (as a smooth vector bundle). Why? Because the vector fields and form a basis of tangent vectors at any point.
Now for the really cool part. Using the connection between stable homotopy theory and framed cobordism theory, it follows that — roughly speaking — the third stable homotopy group of spheres, , is at most !
There are some subtleties here, but they all work out, so skip this paragraph if you want. We need to check that the vector fields can be tweaked slightly to be tangent to the 3-spheres that form the boundary of , and that they then give the ‘standard’ framing of these 3-spheres. We need to notice that a trivialization of the tangent bundle gives a trivialization of the stable normal bundle, which is what really matters for framed cobordism theory. Using the relation between stable homotopy and framed cobordism, our geometric argument then proves that some generator has . So all it proves is that if is a cyclic group generated by , it must either be or where divides . This is what I meant by ‘at most’ . Still, our argument gives us some geometrical understanding of how the number shows up.
For more, see this:
- Tilman, answer to Third stable homotopy group of spheres via geometry?, MathOverflow, November 4, 2010.
I want to find a K3 surface with an explicit, nice smooth vector field with exactly 24 zeros, all of index 1.
To do this, it makes sense to find a K3 surface that has the number 24 built into it. It should be very beautiful. And there’s an obvious choice: ‘the tetrahedral Kummer K3’.
Take the 24-cell: the 4-dimensional regular polytope with 24 vertices and 24 faces. You can think of its vertices as a subgroup of the unit quaternions. This group is called the binary tetrahedral group, because it’s a double cover of the rotational symmetry group of the tetrahedron.
The lattice in the quaternions generated by the vertices of the 24-cell is famous: it’s the D4 lattice (up to a scale factor that doesn’t matter much here). The quotient space is a 4-torus. Since its a compact complex manifold with trivial tangent bundle it’s a Calabi–Yau manifold! Alas, it’s one of those 2-dimensional Calabi–Yau manifolds that we explicitly ruled out in the definition of K3 surface. But notice that it’s a hyper-Kähler manifold, since its tangent spaces are all canonically isomorphic to the quaternions!
So, we’ve got a 2d Calabi–Yau that’s obviously a hyper-Kähler manifold and deeply connected to the number 24. But it’s not a K3 surface.
Luckily people know how to fix this. First, note that is an abelian group so for any point in it there’s a point . Thus, we can form the quotient space
This is a known sort of thing: it’s an example of a Kummer surface. It’s a complex variety, but it’s not smooth at the 16 points coming from points with . These 16 points are singular, and if we draw just a real 2d surface instead of the full complex 2d surface they look like this:

This is a plaster model of a Kummer surface now at the University of Oxford, designed by Karl Rohn, a student of Felix Klein and Alexander Brill.
It turns out that for any Kummer surface, we can ‘minimally resolve’ its 16 singular points and get a smooth complex variety…. which is a K3 surface!
So, we’ve found a beautiful K3 surface with the number 24 built in from the start. Now you just need to find me a vector field on it with exactly 24 isolated zeros, all of index 1.
If you want to know more about this K3 surface, start here:
- Anne Taormina and Katrin Wendland, Symmetry-surfing the moduli space of Kummer K3s.
In Section 1 they discuss the construction of K3 surfaces from Kummer surfaces, which they call Kummer K3s, and they discusses the symmetries of Kummer K3s. The example I just described, called the tetrahedral Kummer K3, is the most symmetrical of them all.
Here’s how its symmetries work. First consider the symmetries of the 4-torus where is the D4 lattice. Remember, this 4-torus is the first step toward building the tetrahedral Kummer K3. Taormin and Wendland call it the tetrahedral torus.
The binary tetrahedral group, called , acts both by right and by left multiplication on the quaternions . Since these actions commute, the right action preserves the hyper-Kähler structure on involving the left action of and . This right action also preserves the D4 lattice , so has a right action on the tetrahedral torus preserving its hyper-Kähler structure. Translations of this 4-torus also preserve the hyper-Kähler structure, and I believe the automorphism group of the tetrahedral torus as a hyper-Kähler manifold is just the semidirect product , no more.
The next step toward building the tetrahedral Kummer K3 is to form the Kummer surface
and the final step is to resolve the singularities in . These steps interact in a nontrivial way with the symmetries of the tetrahedral torus. For example, the group element in maps to , so it acts trivially on . So, the tetrahedral group
acts on and then on the tetrahedral Kummer K3. This is the group of rotational symmetries of a regular tetrahedron. It’s isomorphic to .
Not all translations of the tetrahedral torus act on the tetrahedral Kummer K3. The quotient process, where we set , creates 16 singularities in the Kummer surface, coming from points of that are their own negatives. These points form a subgroup of the , called its ‘2-torsion subgroup’. We can think of this subgroup as ; it’s isomorphic to . This subgroup of translations acts on and then on the tetrahedral Kummer K3.
Putting the pieces together, acts on the tetrahedral Kummer K3. In fact it acts as diffeomorphisms that preserve the hyper-Kähler structure! Indeed, I’m pretty sure from my readings that the automorphism group of the tetrahedral Kummer K3 as a hyper-Kähler manifold is exactly the semidirect product , no more. This group is isomorphic to , so it has
elements.
Note the number 24 is still lurking here, but the 24-element binary tetrahedral group is not acting as symmetries of the tetrahedral Kummer K3. Still, maybe we can use some rather symmetrical construction to build a vector field with 24 zeros of index 1.
This paper gives more details regarding the tetrahedral Kummer K3:
- Anne Taormina and Katrin Wendland, The overarching finite symmetry group of Kummer surfaces in the Mathieu group M24.
In particular, Section 4.2 is all about this surface. They also have other papers on this topic.
Please help me out if you can!
Here are some nice pictures of the real parts of a particular Kummer surface, drawn by Abdelaziz Nait Merzouk.



Re: K3 Surfaces and the Number 24
The MathOverflow sidebar just suggested to me the question of whether there exists an octonionic analogue of a K3 surface, which sounds very like something I’d ask if I had been up too late reading about exception-ology.