Diversity and the Mysteries of Counting

July 30, 2021

Diversity and the Mysteries of Counting

Posted by Tom Leinster

$MathML-enabled post (click for more details).$

Back in 2005 or so, John Baez was giving talks about groupoid cardinality, Euler characteristic, and strange objects with two and a half elements.

I saw a version of this talk at Streetfest in Sydney, called The Mysteries of Counting. It had a big impact on me.

This post makes one simple point: that by thinking along the lines John advocated, we can arrive at the exponential of Shannon entropy — otherwise known as diversity of order $1$ .

$MathML-enabled post (click for more details).$

Background: counting with fractional elements

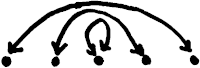
Consider a group $G$ acting on a set $X$ , both finite. How many “pieces” of $X$ are there, modulo $G$ ?

The first, simple, answer is $|X/G|$ , the number of orbits. For example, in the action of $C_2$ on the five-element set shown in the diagram above, this gives an answer of $3$ .

But there’s a second answer: $|X|/|G|$ , the cardinality of $X$ divided by the order of $G$ . If the action is free then this is equal to $|X/G|$ , but in general it’s not. For instance, in the example shown, this gives an answer of $2\tfrac{1}{2}$ .

The short intuitive justification for this alternative answer is that when counting, we often want to quotient out by the order of symmetry groups. For example, there are situations in which a point with an $S_n$ -action deserves to count as only $1/n!$ elements. John’s slides say much more on this theme.

This second answer also fits into an abstract framework.

Every action of a group on a set gives rise to a so-called action groupoid $X/\!/G$ . Its objects are the elements of $X$ , and a map $x \to y$ is an element $g \in G$ such that $g x = y$ . Equivalently, it’s the category of elements of the functor $G \to Set$ corresponding to the group action.

There is a notion of the cardinality $|A| \in \mathbb{Q}$ of a finite groupoid $A$ . And when you take the cardinality of this action groupoid, you get exactly $|X|/|G|$ . That is:

$|X/\!/G| = |X|/|G|.$

In summary, the first answer to “how many pieces are there?” is $|X/G|$ , and the second is $|X/\!/G|$ .

Now let’s do the same thing with monoids in place of groups. Let $M$ be a monoid acting on a set $X$ , and assume they’re both finite whenever we need to. How many “pieces” of $X$ are there, modulo $M$ ?

Again, the obvious answer is $|X/M|$ . Here $X/M$ is again the set of orbits. (You have to be a bit more careful defining “orbit” for monoids than for groups: the equivalence relation on $X$ is generated, not defined, by $x \sim y$ if there exists $m \in M$ such that $m x = y$ .)

And again, there’s a second, alternative answer: $|X|/|M|$ .

The abstract framework for this second answer is now about categories rather than groupoids. Every action of a monoid on a set gives rise to an action category $X/\!/M$ . It has the same explicit and categorical descriptions as in the group case.

There is a notion of the Euler characteristic or magnitude $|A| \in \mathbb{Q}$ of a finite category $A$ . It could equally well be called “cardinality”, and generalizes groupoid cardinality. And when you take the Euler characteristic of this action category, you get $|X|/|M|$ . That is:

$|X/\!/M| = |X|/|M|.$

So just as for groups, the first and second answers to “how many pieces are there?” are $|X/M|$ and $|X/\!/M|$ , respectively.

How diversity emerges

Take a surjective map of sets $\pi: A \to I$ . We’re going to think about two structures that arise from $\pi$ :

The monoid $End_I(A)$ of endomorphisms of $A$ over $I$ (that is, making the evident triangle commute). The monoid structure is given by composition.
The set $End(A)$ of all endomorphisms of $A$ . We could give this a monoid structure too, but we’re only ever going to treat it as a set.

The monoid $End_I(A)$ acts on the set $End(A)$ on the left, by composition: an endomorphism of $A$ followed by an endomorphism of $A$ over $I$ is an endomorphism over $A$ . (The fact that one of them is over $I$ does nothing.)

So, how many pieces of $End(A)$ are there, modulo $End_I(A)$ ?

The first answer is “count the number of orbits”. How many orbits are there?

It’s not too hard to show that there’s a canonical isomorphism

$\frac{End(A)}{End_I(A)} \cong I^A,$

where the right-hand side is the set of functions $A \to I$ . It’s a simple little proof of a type that doesn’t work very well in a blog post. You start with the fact that composition with $\pi$ gives a map $End(A) \to I^A$ and take it from there.

So assuming now that $A$ and $I$ are finite, the number of orbits is given by

$\biggl| \frac{End(A)}{End_I(A)} \biggr| = |I|^{|A|}.$

That’s the first answer, but while we’re here, let’s observe that this equation can be rearranged to give a funny formula for the cardinality of $I$ :

$|I| = \biggl| \frac{End(A)}{End_I(A)} \biggr|^{1/|A|}.$

The second, alternative, answer is that the number of pieces is

$\frac{|End(A)|}{|End_I(A)|}.$

What is this, explicitly? Write the fibre $\pi^{-1}(i)$ as $A_i$ . Then

$|End(A)| = |A|^{|A|}, \quad |End_I(A)| = \prod_{i \in I} |A_i|^{|A_i|},$

and since $A = \coprod_{i \in I} A_i$ , this gives

$\frac{|End(A)|}{|End_I(A)|} = \prod_{i \in I} \biggl( \frac{|A|}{|A_i|} \biggr)^{|A_i|}$

as our second answer.

Now here’s the punchline. The first answer gave us a formula for the cardinality of $I$ :

$|I| = \biggl| \frac{End(A)}{End_I(A)} \biggr|^{1/|A|}.$

What’s the analogous formula for the second answer? That is, in the equation

$? = \biggl(\frac{|End(A)|}{|End_I(A)|}\biggr)^{1/|A|},$

what goes on the left-hand side?

Well, it’s

$\prod_{i \in I} \biggl( \frac{|A|}{|A_i|} \biggr)^{|A_i|/|A|}.$

We can simplify this if we write $p_i = |A_i|/|A|$ . These numbers $p_i$ are nonnegative and sum to $1$ , so they amount to a probability distribution

$\mathbf{p} = (p_i)_{i \in I} = (|A_i|/|A|)_{i \in I}.$

The formula for “?” then simplifies to

$\prod_{i \in I} p_i^{-p_i}.$

And this is nothing but the exponential of Shannon entropy, also called the diversity or Hill number $D_1(\mathbf{p})$ of order $1$ .

In conclusion, if we take that first-answer formula for the cardinality of $I$ —

$|I| = \biggl| \frac{End(A)}{End_I(A)} \biggr|^{1/|A|}$

— then its second-answer analogue is a formula for the diversity of $\mathbf{p}$ —

$D_1(\mathbf{p}) = \biggl(\frac{|End(A)|}{|End_I(A)|}\biggr)^{1/|A|}.$

And this is yet another glimpse of an analogy that André Joyal first explained to me one fateful day in Barcelona in 2008: exponential of entropy is a cousin of cardinality.

Posted at July 30, 2021 11:42 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3339

29 Comments & 0 Trackbacks

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Beautiful!

I learned about the diversity of order 1 while reading Shannon’s seminal paper and I always liked it more than the entropy because it has the nice interpretation as “the probability of a typical event”, and because it has the form of the “endomorphism number of the probability distribution” if you squint and pretend that everything you can do in the biclosed equipment of spans works for good ol’ matrices as well. I mentioned this to David Spivak at some point and he came back and told me about this counting endomorphisms story which requires significantly less squinting, but still had a pesky division where it shouldn’t be.

This is a great explanation of why that pesky division really should be there!

This makes me wonder: what other quantities and ways of doing things from basic information theory and probability theory can be described “objectively” with the combinatorics of surjections of finite sets like this?

Posted by: David Jaz Myers on July 30, 2021 5:21 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Thanks!

Where in Shannon’s paper do you mean?

Posted by: Tom Leinster on July 30, 2021 5:38 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

It’s Section 7 in this paper. Shannon defines

$p = p_1^{p_1N}\cdots p_{n}^{p_n N}$

to be roughly the probability of a typical series of length $N$ . But this is

$p = \left(\prod_i p_i^{p_i}\right)^N$

which let’s us imagine that to draw a typical series we independently draw a “typical event” (even though strictly speaking this is non-sensical). The entropy is then the number of bits needed to encode a typical event.

Shannon doesn’t say it in exactly this way, probably because the idea of a “typical event” is non-sensical on its own, but the story is there.

Posted by: David Jaz Myers on July 30, 2021 7:01 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Got it. Thanks.

Posted by: Tom Leinster on July 30, 2021 7:07 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

By the way, I imposed the hypothesis that $\pi: A \to I$ is surjective, which means that the probabilities $p_i = |\pi^{-1}(i)|/|A|$ are nonzero. If you drop this hypothesis, the equation

$|I| = \biggl| \frac{End(A)}{End_I(A)} \biggr|^{1/|A|}$

becomes

$|im(\pi)| = \biggl| \frac{End(A)}{End_I(A)} \biggr|^{1/|A|}.$

And $|im(\pi)|$ is equal to the cardinality of the support of $\mathbf{p}$ , also known as the diversity of order $0$ of $\mathbf{p}$ .

So this line of thought gives us the diversities of order $0$ and $1$ .

I have no idea whether there’s also a place in this story for diversity of order $q$ for other values of $q$ .

Posted by: Tom Leinster on July 30, 2021 6:07 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

This might be silly, but if you work with vector spaces then $\left|\mathrm{End}(V)\right|=\left|V\right|^2$ , and so you might get something like $q = 2$ .

Posted by: Oscar Cunningham on August 1, 2021 1:04 AM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Can the concept of Euler characteristic be extended to categories with an infinite number of objects and an infinite number of morphisms between objects?

Posted by: Madeleine Birchfield on July 30, 2021 9:10 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Infinitely many objects and finite homsets: yes, under favourable conditions. John, along with Jim Dolan, studied infinite groupoids with well-defined Euler characteristic (cardinality). An appealing example is the groupoid of finite sets and bijections, whose Euler characteristic is

$\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \cdots = e.$

For categories that aren’t groupoids, Section 3 of this paper goes into the situation in some detail.

But if the homsets are infinite, that’s another matter. I don’t know of a decent way of defining Euler characteristic in that case, unless the homsets have further structure (e.g. a topology).

The point is that for $V$ -enriched categories, the definition of Euler characteristic (or magnitude, as it’s usually called at this level of generality) requires a preexisting notion of the “size” of objects of $V$ . In other words, a notion of size for objects of $V$ gives rise to a notion of size for categories enriched in $V$ .

Posted by: Tom Leinster on July 30, 2021 9:31 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Is there some way to leverage into the account here something from your post – A Visual Telling of Joyal’s Proof Of Cayley’s Formula?

For $A$ as here

the number of vertebrates (bipointed trees) on $A$ is equal to the number of endofunctions of $A$ .

Then if $A \to I$ is an $I$ -colouring of $A$ , is there anything interesting about the bipointed trees that arise from a colour-preserving endofunction of $A$ ?

$Tree_{\ast\ast} \cong Ord \circ Tree_{\ast},$

perhaps we might require the pointed trees to be monochrome.

Posted by: David Corfield on July 31, 2021 8:49 AM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Interesting question. I haven’t thought about that. But it had occurred to me that there should be more to say about the canonical isomorphism

$\frac{End(A)}{End_I(A)} \cong I^A$

for surjective maps of sets $\pi: A \to I$ , or more generally

$\frac{End(A)}{End_I(A)} \cong im(\pi)^A$

for arbitrary maps of sets $\pi: A \to I$ . (In both cases, the denominator could more precisely be written as $End_I(\pi)$ .)

I immediately decategorified, which is why I have a lingering feeling that there’s more to say. Perhaps species provide the right kind of setting.

Posted by: Tom Leinster on July 31, 2021 11:18 AM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

I was thinking about that case. In information terms, it’s rather like trying to specify an endomorphism on a set of coloured elements, and just being given the colour of the image of each element.

As a concrete case, the easiest example where the cardinalities diverge is (I think) when there’s a 3-element set mapping surjectively to a 2-element set. So there are 27 endomorphisms, 4 of which preserve the fibres. There are 8 ways to specify the fibres of images, and yet the action category has cardinality $27/4$ .

How should we think about these sizes even in the simple case of John’s that you begin the post with, 5 elements acted on by symmetry? For me to specify one of the 5, I can first say which of the 3 classes it’s in. But is there anything information-theoretic about the cardinality $5/2$ ?

Posted by: David Corfield on July 31, 2021 11:48 AM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

If you try to break down the cardinality 27/4 by orbit, you’ll find several parts with cardinality less than 1. I assume this means negative information, like some of it is leaking away into the size of M.

To use the opening example: we could have $C_100$ act on the five-element set to give the same 3 orbits, but a much smaller cardinality.

Posted by: unekdoud on August 10, 2021 3:48 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Say we have $A = \{a,b,c\}$ , $I =\{1,2\}$ , with $a$ and $b$ in the fibre over $1$ and $c$ in the fibre over $2$ .

I can provide information on, $f$ , an endomorphism of $A$ , by specifying the fibres of each of $f(a), f(b), f(c)$ .

There are $|I|^{|A|}= 2^3$ possibilities, but some are more informative than others. If I say $(2,2,2)$ , then you know that $f$ sends all of $A$ to $c$ . If I say $(1,1,1)$ , then there are still $8$ possible $f$ s.

The monoid of the $4$ endomorphisms of $A$ which preserve fibres acts on the $27$ endomorphisms, yielding the $8$ classes of images on $I$ . But counting the action category cardinality, we find the component $(2,2,2)$ contributing $\frac{1}{4}$ , while the component $(1,2,2)$ contributes $\frac{1}{2}$ . These sizes sum to $\frac{27}{4}$ .

More generally for $A$ and $I$ of given sizes, you’d want the fibres to be evenly sized to provide as much information as possible by minimizing fibre-preserving endomorphisms. I’m reminded of Lawvere’s observables in Functorial remarks on the general concept of chaos, p. 3.

Posted by: David Corfield on August 11, 2021 8:18 AM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

So $|I| \geq D_1(\mathbf{p})$ . Equality is achieved when $A$ maps evenly onto $I$ .

Posted by: David Corfield on August 11, 2021 9:15 AM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

In the functional digraph of the endofunction, the connected components are the orbits. So if it’s colour-preserving, the colour is constant on each component.

In Joyal’s bijection with doubly rooted trees you chop up the digraph and reassamble it to build the tree, so some of this structure is still visible. The rooted trees you get in the decomposition $\mathrm{Tree}_{\ast\ast} = \mathrm{Ord} \circ \mathrm{Tree}_\ast$ will indeed be monochrome, but that’s not a full characterization. You also need that when the ordering is reinterpreted as a permutation (which of course requires a non-canonical choice of an ordering of the labels) that permutation is colour-preserving. I don’t think there’s any nicer way to rephrase that condition.

Posted by: lambda on July 31, 2021 9:32 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

What would relative entropy be from this point of view? Suppose the other probability distribution is given by a set $B\to I$ . Then my first guess was to look at the action of $\mathrm{End}_I(A)$ on $\mathrm{Hom}_I(A,B)$ . But that can’t quite be right because the entropy of $p$ isn’t the relative entropy with respect to itself, it’s the relative entropy relative to the uniform distribution, corresponding to the identity on $I$ .

Posted by: Oscar Cunningham on July 31, 2021 11:39 AM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Thinking about it further, if we let $A\to I$ and $B\to I$ with $p_i = A_i/A$ and $q_i = B_i/B$ then $\exp(D(p\parallel q))^A = \frac{\left|\mathrm{Hom}(A,B)\right|\left|\mathrm{End}_I(A)\right|}{\left|\mathrm{Hom}_I(A,B)\right|\left|\mathrm{End}(A)\right|}.$

To make this amenable to thinking of in terms of cardinality, we could rewrite it as $\frac{\left|\mathrm{Hom}(A,B)\right|/\left|\mathrm{End}_I(B)\right|}{\left(\left|\mathrm{Hom}_I(A,B)\right|/\left|\mathrm{End}_I(B)\right|\right)\left(\left|\mathrm{End}(A)\right|/\left|\mathrm{End}_I(A)\right|\right)}$ but then the analogous quantity $\frac{\left|\mathrm{Hom}(A,B)/\mathrm{End}_I(B)\right|}{\left|\mathrm{Hom}_I(A,B)/\mathrm{End}_I(B)\right|\left|\mathrm{End}(A)/\mathrm{End}_I(A)\right|}$ has size $\frac{\left|I\right|^\left|A\right|}{1\left|I\right|^\left|A\right|} = 1$ which is a bit boring.

Posted by: Oscar Cunningham on July 31, 2021 8:28 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

I couldn’t get anywhere with this either. Did some playing around along similar lines but to no avail. It’s an interesting idea, though.

Posted by: Tom Leinster on July 31, 2021 8:49 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

One quick very undeveloped thought. Taking $A$ as a discrete topological space, the $\pi^{-1}(i)$ form a cover. Then there’s the world of topological entropy which looks to gauge the entropy of an endomap, $f$ , relative to the cover, $C$ .

Usually one maximises over $C$ for a fixed $f$ . Is it possible that here we’re fixing $C$ and averaging over all $f$ ? Or something like that.

Posted by: David Corfield on July 31, 2021 5:22 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

It seems that “symbolic dynamics” is the term used for the study of the dynamics of a system by partitioning the state space, labelled by “symbols”. Then orbits correspond to sequences of symbols. These would have to repeat after $|A|$ iterations, so $|I|^{|A|}$ would be the maximum number of different symbol sequences.

There’s an old paper I remember by Chris Hillman, An entropy primer, and it talks of the entropy of a partition (p. 5). This later on (Sec. 8) bounds a source entropy.

Posted by: David Corfield on August 1, 2021 9:52 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Re the action categories [X//M] at the beginning of this thread: does it make any sense to ask about the information loss associated to the forgetful functor

[X//M] —> [(X/M)//1] ?

(I sometimes believe in the axiom of choice, and that this is an equivalence when G is a group?)

Posted by: jackjohnson on August 1, 2021 8:34 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

Sorry, only just got to this. But I’m confused. Isn’t the category $(X/M)/\!/1$ discrete, in the sense that the only maps in it are identities? So what’s the functor $[X/\!/M] \to [(X/M)/\!/1]$ ?

Posted by: Tom Leinster on August 5, 2021 2:40 PM | Permalink | Reply to this

Re: Diversity and the Mysteries of Counting

$MathML-enabled post (click for more details).$

I only saw this just now, sorry for not replying sooner. Maybe I misunderstand the situation for monoids in general?

I’m thinking of the construction which sends a groupoid to its skeleton, ie if M = G then

[X//G] = \coprod_{z \in X/G} [{z}//iso(z)]

(where iso(z} is the isotropy group of a representative of the equivalence class z) innit? I would think that the construction which collapses equivalence classes loses information, but information loss is an unfamiliar topic for me.

Posted by: jackjohnson on August 10, 2021 12:35 AM | Permalink | Reply to this

The sizes of “type classes”

$MathML-enabled post (click for more details).$

Consider permutations instead of endomorphisms, which means replacing appearances of $n^n$ with $n!$ . Then your formulae for $D_1$ pretty much turns into the approximation for entropy in Elements of Information Theory by Cover and Thomas around p.350. In particular, $\frac{|\End(A)|}{|\End_I(A)|}$ is replaced by a multinomial coefficient. The fact that this is a good approximation comes from the Stirling formula.

Posted by: Dan Piponi on August 2, 2021 6:03 PM | Permalink | Reply to this

Re: The sizes of “type classes”

$MathML-enabled post (click for more details).$

Aha, thanks. I hadn’t come across that part of Cover and Thomas before.

For future reference, let me note down what seem to be the main points. This is from the second edition of C&T, Section 11.1.

Given a finite set $\mathcal{X}$ (an “alphabet”) and a sequence $\mathbf{x} = (x_1, \ldots, x_n)$ of elements, the type of $\mathbf{x}$ is what I know as the empirical distribution of $\mathbf{x}$ . That is, it’s the probability distribution on $\mathcal{X}$ that gives probability $k/n$ to an element of $\mathcal{X}$ appearing $k$ times in the sequence.
Fix $n$ . There’s an equivalence relation on $\mathcal{X}^n$ defined by saying that two sequences are equivalent if they have the same type. The equivalence classes are called type classes. If $P$ is a type, then the equivalence class consisting of all sequences of type $P$ is written as $T(P)$ .
For example, if $\mathcal{X} = \{1, 2, 3\}$ and $n = 5$ then one of the type classes consists of all the 5-tuples of elements of $\{1, 2, 3\}$ containing three 1s, one 2 and one 3. So if we write $P = (3/5, 1/5, 1/5)$ then $T(P)$ is this set, which has $\binom{5}{3, 1, 1} = 20$ elements.
Theorem 11.1.3 states that $\frac{1}{(n + 1)^{|\mathcal{X}|}} D_1(P)^n \leq |T(P)| \leq D_1(P)^n.$ As Dan says, the proof is mostly about Stirling’s approximation.

Posted by: Tom Leinster on August 5, 2021 2:56 PM | Permalink | Reply to this

Re: The sizes of type classes

$MathML-enabled post (click for more details).$

I’ve long thought that the “type theorem” is a bit underrated. To me it’s a very direct expression of what entropy is: a measure of how the number of combinations of something is reduced by sorting the things into buckets (“types”). But it’s not exact, unlike your formula. So I found your article very interesting.

Posted by: Dan Piponi on August 7, 2021 5:53 AM | Permalink | Reply to this

Re: The sizes of “type classes”

$MathML-enabled post (click for more details).$

I guess this is obvious to everyone who is really tuned into this discussion, but if we replace endomorphisms by permutations as Dan suggests, then

$\frac{|End(A)|}{|End_I(A)|}$

gets replaced by what I’ll call

$\frac{|Aut(A)|}{|Aut_I(A)|}$

where $Aut(A)$ is the group of permutations of the finite set $A$ , while $Aut_I(A)$ is the subgroup consisting of permutations that preserve each fiber of $\pi\colon A \to I$ .

This is an example of groupoid cardinality:

$\frac{|Aut(A)|}{|Aut_I(A)|} = \left| Aut(A)//Aut_I(A)\right|$

where $Aut(A)//Aut_I(A)$ is the action groupoid created by the action of $Aut_I(A)$ on $Aut(A)$ .

Which action? It has a left action, a right action, and an action by conjugation! So there are really three action groupoids, but the formula above is true for any of these.

In some ways the conjugation action is nicest, because then $Aut_I(A)$ acts as group automorphisms on $Aut(A)$ , so $Aut(A)//Aut_I(A)$ is better than a groupoid: it’s a 2-group! That’s a categorified version of a group.

On the other hand, in Tom’s related formula

$\frac{|End(A)|}{|End_I(A)|} = \left|End(A)//End_I(A)\right|$

the monoid $End_I(A)$ can only act on $End(A)$ on the left or the right. So, if we’re trying to understand the relation between $Aut(A)//Aut_I(A)$ and $End(A)//End_I(A)$ — which seems like a good thing to understand! — we should probably use the right or left action of $Aut_I(A)$ on $Aut(A)$ . I don’t think it matters much which of these we use; Tom chose the left action.

Understanding the relation between $Aut(A)//Aut_I(A)$ and $End(A)//End_I(A)$ might provide a new look at the ‘type theorem’ in Cover and Thomas, and maybe a better understanding of entropy.

Posted by: John Baez on August 11, 2021 12:49 AM | Permalink | Reply to this

Re: The sizes of “type classes”

$MathML-enabled post (click for more details).$

John wrote:

the monoid $End_I(A)$ can only act on $End(A)$ on the left or the right […] I don’t think it matters much which of these we use; Tom chose the left action.

It’s only for the left action that the natural isomorphism

$\frac{End(A)}{End_I(A)} \cong I^A$

holds. In words (mostly): a function $A \to I$ amounts to an endomorphism of $A$ , modulo endomorphisms of $A$ over $I$ . That’s only true if you interpret “modulo” with respect to the left action.

As I said in the post, the isomorphism is induced by composition with the surjection $\pi: A \to I$ :

$\pi \circ -: End(A) \to I^A.$

It’s a series of easy exercises to show that $\pi \circ -$ is surjective and that the equivalence relation it induces on $End(A)$ is the same as that induced by the left action of the monoid $End_I(A)$ . (These exercises are made easier by choosing a section of $\pi$ .) So $\pi \circ -$ induces an isomorphism

$\frac{End(A)}{End_I(A)} \cong I^A.$

That’s all for the left action of $End_I(A)$ on $End(A)$ . I don’t know what $End(A)/End_I(A)$ is for the right action, but I’m pretty sure it’s not $I^A$ , and my guess is that it’s not very interesting.

Posted by: Tom Leinster on August 11, 2021 11:10 AM | Permalink | Reply to this

Re: The sizes of “type classes”

$MathML-enabled post (click for more details).$

While I’m at it, let me write down the translation of the Cover and Thomas type theorem into the notation of this post.

Their sequence $\mathbf{x}: \{1, \ldots, n\} \to \mathcal{X}$ is what I’m calling $\pi: A \to I$ . (I assumed $\pi$ to be surjective, which simplifies things a bit but isn’t essential.) Their distribution $P$ on $\mathcal{X}$ is my distribution $\mathbf{p}$ on $I$ , given by $p_i = |\pi^{-1}(i)|/|A|$ .

The number of elements of the type class $T(P)$ is given by

$|T(P)| = \frac{|A|!}{\prod |\pi^{-1}(i)|!} = \frac{|Aut(A)|}{|Aut_I(A)|} = \bigl| Aut(A) /\!/ Aut_I(A) \bigr|,$

where the last pair of bars means cardinality of a groupoid. And I showed in my post that

$D_1(\mathbf{p})^{|A|} = \frac{|End(A)|}{|End_I(A)|} = \bigl| End(A) /\!/ End_I(A) \bigr|,$

where the last pair of bars means magnitude of a category. So the theorem

$\frac{1}{(n + 1)^{|\mathcal{X}|}} D_1(P)^n \leq |T(P)| \leq D_1(P)^n$

in Cover and Thomas can be expressed as

$\frac{1}{(|A| + 1)^{|I|}} \leq \frac{|Aut(A) /\!/ Aut_I(A) |}{|End(A) /\!/ End_I(A)|} \leq 1,$

where all the bars in the middle term are again magnitudes of categories (and I’ve divided by $D_1(P)^n$ throughout). This result holds for every surjection $\pi: A \to I$ of finite sets.

Posted by: Tom Leinster on August 11, 2021 3:33 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

July 30, 2021