A Joyal-Type Proof Of The Number Of Nilpotents
Posted by Tom Leinster
Let be a finite set. What’s the probability that a random endofunction of is eventually constant — that is, becomes constant after you iterate it enough times? It’s . That’s basically Cayley’s tree formula, Joyal’s beautiful proof of which I showed you recently.
Now suppose that has the structure of a vector space. What’s the probability that a random linear operator on is eventually constant — or as one usually says, nilpotent? It’s still . I recently showed you a proof of this using generating functions, but it gave no indication of why the answer is as simple as it is. There was some miraculous cancellation.
Today I’ll show you a much more direct proof of the probability of getting a nilpotent, or equivalently the number of nilpotents. The argument shadows Joyal’s proof of Cayley’s formula.
First let me explain what I just said about the probability of a random endofunction being eventually constant, and why the answer is essentially Cayley’s formula.
Let be a finite set. A function is eventually constant if is constant for some , or equivalently is constant for all , or equivalently has only one periodic point (which must then be a fixed point). An eventually constant function looks like this:

Here I’ve drawn an arrow from to for every , except when is the eventual constant value, which I’ve circled and coloured in pink. Actually, the arrows add no information, because they all flow in the direction towards the pink vertex. So we might as well remove them:

What we have now is just a rooted tree with as its set of vertices. Cayley’s formula tells us how many unrooted trees there are with vertex-set : there are of them, where . Hence there are rooted trees, or equivalently eventually constant endofunctions of . But since there are endofunctions of in all, the probability that a randomly-selected endofunction is eventually constant is
That’s the situation for plain, unadorned sets. But this post is about vector spaces. Of course, when we’re dealing with vector spaces we only consider the linear endomorphisms, and by linearity, the eventually constant ones are exactly the nilpotents. So:
nilpotent operators are the linear analogue of rooted trees.
The root of the tree corresponds to the origin of the vector space.

I’m going to show you a proof that a random linear operator on a finite vector space is eventually constant (nilpotent) with probability .
First, though, let me mention a mystery, in the hope that someone can shed some light. You’ll have noticed from the beginning of the post that two probabilities are the same: for a finite vector space , the probability of a random endomorphism being eventually constant isn’t affected by whether we’re consider all endofunctions or just the linear ones. In probabilistic notation,
P(eventually constant | linear) = P(eventually constant).
So the conditions “eventually constant” and “linear” on an endofunction are independent, in the sense of probability theory. I have no intuition for why this should be true. Does anyone else?
Background linear algebra
For the proof, we’ll need a few linear algebra facts that are absolutely elementary and general, but not as well-known as they could be.
One way in which vector spaces are more complex than sets is that every subset of a set has just one complement, a subspace of a vector space has many. By a “complement” of a linear subspace I mean what’s usually called a complementary subspace, that is, another subspace such that and is the whole space.
So, given a subspace of and any two subspaces complementary to —
— it may be that and are not equal. However, they are canonically isomorphic. Indeed, we have projection maps
both with kernel , so by the first isomorphism theorem, there’s a unique isomorphism commuting with the projections:

For a point of , we can characterize as the unique point of such that . So moves points in a direction parallel to .
Now here’s a crucial fact: for vector spaces and ,
subspaces of complementary to .
This correspondence is given from left to right by the graph construction. That is, given a linear map , we have its graph
which is a subspace of complementary to .
Conversely, given a subspace of complementary to , we have the canonical isomorphism defined above — and as we noted, it gives a map from to . All we’re doing here is reading a function off from its graph in the usual way. Starting from a point , you take the unique point on the graph () that’s above , and then .
Aside From this correspondence we can easily work out how many complements any given subspace has, if we’re talking about finite-dimensional spaces over finite fields. Let be a -dimensional subspace of an -dimensional space over a field with elements. Choose, arbitrarily, a complementary subspace of in . Then the fact just proved implies that there are the same number of complementary subspaces of in as there are linear maps . Since , there are such maps. Hence has complements.
This formula fits with the folklore idea that a vector space over the mythical field with one element is a set (or should I say pointed set?). For if we put in the formula just established, we come to the conclusion that a subset of a set has exactly complement — which is indeed correct.
The next linear algebra fact we’ll need is this:
That is, for any linear operator on a finite-dimensional vector space (over any field), there are unique subspaces and of such that:
- restricts to a nilpotent operator on
- restricts to an automorphism of .
For today it doesn’t matter what and actually are, but if you’re interested you can find the answer here or here: they’re the eventual kernel and eventual image, respectively.
Finally, it’s a fact that for any finite-dimensional vector space , there’s a (non-canonical) bijection
ordered bases of .
This is closely analogous to the fact that for a finite sets, the permutations are in bijection with the total orders. Both are proved using a torsor argument: we’ve got a group acting freely and transitively on a nonempty set, which implies that the group and set are in bijection.
Concretely, in this case, the proof goes like this. Choose an ordered basis of . For any automorphism of , we get a new ordered basis . And it’s easy to see that the assignment defines a bijection between automorphisms and ordered bases.
Pre-proof throat-clearing
Let be a finite-dimensional vector space over any field. Write and for the set of nilpotent operators on and endomorphisms of (linear operators on) . We’re going to show that there’s a bijection
When the base field is finite, this immediately implies that the probability of a random linear operator on being nilpotent is . It also gives a formula for the number of nilpotents on . For if is -dimensional over a field with elements, there are linear operators on , since to specify one we have to choose for each of basis elements one of the elements of . Hence there are
nilpotents on .
The bijection is not canonical. We’re going to need to choose, for each linear subspace of :
- a complementary subspace
- a bijection between the ordered bases of and the automorphisms of .
If we were working over or then we could choose the complementary subspaces by choosing an inner product on — but we’re probably not. In any case, it’s certainly true that every subspace has at least one complement, and we can just choose arbitrarily.
Aside The situation in Joyal’s proof of Cayley’s formula is very similar. There, to get a bijection between endomorphisms and vertebrates (bipointed trees), we have to choose for each subset a bijection between the total orders on and the permutations of . It’s unsurprising that we don’t also have to choose a complement of , since in the world of sets, subsets have a unique complement anyway!
Once these choices have been made, we get a bijection between and as follows.
The proof
Start with a pair , consisting of a nilpotent on and an element of :

(I don’t want to clutter up this proof with further discussion of the analogy with Joyal’s proof of Cayley’s formula, but I’ve chosen the colours in these diagrams to match the ones in my presentation of Joyal’s proof. For full effect, you might want to open that post in another window and look at the two arguments side by side.)
Since is nilpotent, there’s a least such that . It’s easy to show that
are linearly independent, so they form a basis for the subspace that they span. Here’s a picture with :

(This picture shouldn’t be taken too seriously: I’ve drawn as if it were one-dimensional, in which case there’s no way we can have .)
Let’s write :

It looks as if we’ve thrown away , but we haven’t: we recover it from the ordered basis as if , or as otherwise.
Now is completely determined on by , since it’s given by if , and by . So given and its ordered basis , to specify we only need to specify its restriction to . This restriction is a map , which in turn is determined by its two components
So, our original pair is uniquely determined by the subspace , its ordered basis , and the linear maps and . The original operator is nilpotent iff is nilpotent, as you can easily check. (The background fact is this: given a linear operator on a direct sum such that , and writing for its block decomposition, is nilpotent iff and are nilpotent.) So what we’ve now got is data like this:
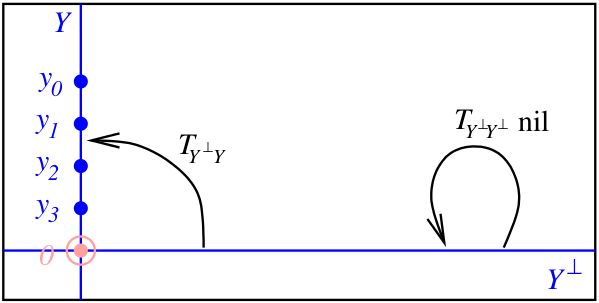
We saw earlier that linear maps correspond one-to-one with subspaces of complementary to , via the graph construction. So we can equivalently replace by a subspace of complementary to :
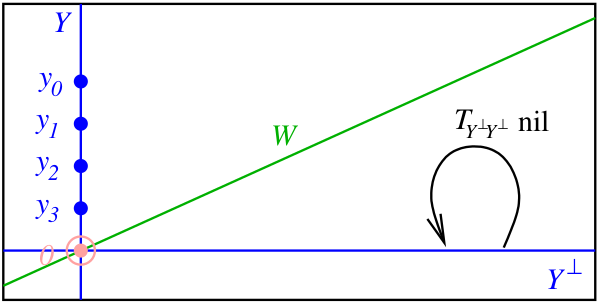
On the other hand, we also saw that and — both being subspaces of complementary to — are canonically isomorphic. So we can equivalently replace the nilpotent operator on by a nilpotent operator on :
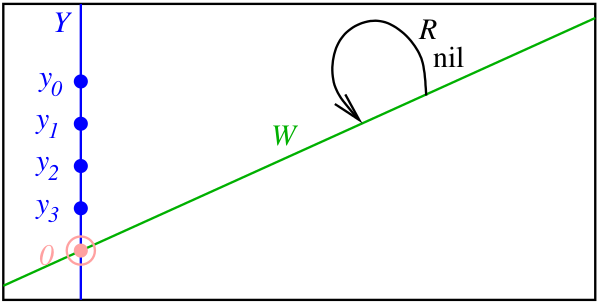
Next, ordered bases of are in bijection with automorphisms of . (There’s no canonical bijection, but that’s OK: we chose one earlier.) So we can equivalently replace the ordered basis by an automorphism of :

So far we’ve shown that
pairs (nilpotent on , element of )
are in bijection with
quadruples (subspace of , nilpotent on , subspace of , automorphism of ) with .
But since every linear operator on decomposes uniquely as the direct sum of a nilpotent and an automorphism, such quadruples are in canonical bijection with linear operators on :

Hence pairs (nilpotent on , element of ) are in bijection with endomorphisms of :
as required.

Re: A Joyal-Type Proof Of The Number Of Nilpotents
Some historical comments: the theorem on the number of nilpotents on a finite vector space (or equivalently the probability that a random linear operator is nilpotent) was apparently first proved by Fine and Herstein:
Their proof is surprisingly complicated and computational. By 2006, things were much more streamlined, as shown by this paper of Crabb:
Crabb gives a quick slick proof there, which I haven’t yet absorbed.