The n-Category Café

Let’s dive straight in with an inductive definition. Take a well-ordered set $W$. Then $\beth_W$ is said to exist if $\beth_V$ exists for all well-ordered sets $V \prec W$ and there is some infinite set $X$ such that $2^{\beth_V} \leq X$ for all $V \prec W$. In that case, $\beth_W$ is defined to be the smallest such set $X$.

To digest this definition, it helps to think about the three different kinds of well-ordered set. These are:

• The empty well-ordered set.

• Successors. These are the well-ordered sets that can be expressed as $V^+$ for some other well-ordered set $V$. (Recall that $V^+$ means $V$ with a new greatest element adjoined.) The successors can also be characterized as the well-ordered sets with a greatest element.

• Limits. These are the well-ordered sets that are not successors. There seems not to be agreement over whether the empty well-ordered set should count as a limit; I haven’t acquired an opinion on this yet, but I’d be happy to be told what my opinion should be. Anyway, they’re the (nonempty?) well-ordered sets with no greatest element.

The corresponding beths look like this.

• Taking $W$ to be the empty well-ordered set $0$ in the definition of beth tells us that $\beth_0$ does exist, and that it’s the smallest infinite set — namely, $\mathbb{N}$. The sole reason why the word “infinite” is in the definition of beth is to make $\beth_0$ be equal to $\mathbb{N}$ rather than $\emptyset$. That’s just convention; I see no compelling reason to begin the beths at $\mathbb{N}$ rather than $\emptyset$.

• Suppose that $W$ is a successor, say $W = V^+$. If $\beth_V$ exists then $\beth_W$ also exists, with $\beth_W = 2^{\beth_V}$.

• Suppose that $W$ is a limit. In order for $\beth_W$ to exist, it must certainly be the case that $\beth_V$ exists for all $V \prec W$. That doesn’t guarantee that $\beth_W$ exists, but if it does, it’s the least upper bound of these sets $\beth_V$: $$\beth_W = \sup_{V \prec W} \beth_V.$$

For example,

$$\beth_0 = \mathbb{N}, \ \beth_1 = 2^\mathbb{N}, \ \beth_2 = 2^{2^{\mathbb{N}}}, \ldots.$$

Here $\beth_n$ means $\beth_{\mathbf{n}}$, where $\mathbf{n}$ is the unique $n$-element well-ordered set. And $\beth_\omega$, if it exists, is the supremum of $\beth_0, \beth_1, \ldots$.

This inductive definition of the beths is slightly tricky, in that it’s simultaneously an inductive definition of the existence of $\beth_W$ and of what the set $\beth_W$ actually is. Here’s a non-inductive alternative.

The idea is that if $\beth_W$ exists then we should be able to directly characterize the family of sets

$$(\beth_V)_{V \preceq W},$$

the last member of which is $\beth_W$ itself. Now I’ve been a bit slack in the indexing here, because it should really be over the isomorphism classes of well-ordered sets $V \preceq W$. But that’s easily overcome: every well-ordered set $V \preceq W$ is isomorphic to

$$↡ w = \{ v \in W : v \lt w \}$$

for a unique $w \in W^+$. So strictly speaking, our family is

$$(\beth_{↡ w})_{w \in W^+}.$$

And in ETCS, families are expressed as maps into the indexing set, so the picture is this:

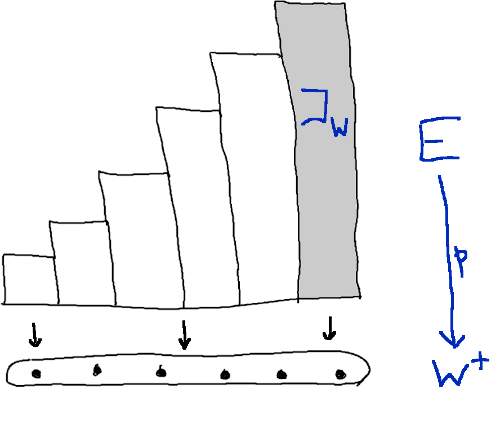
Formally, let $W$ be a well-ordered set. Then $\beth_W$ exists if and only if there exist a set $E$ and a function $p: E \to W^+$ with the following property:

for all $w \in W$, the fibre $p^{-1}(w)$ is the least infinite set $\geq 2^{p^{-1}(v)}$ for all $v \lt w$.

In that case, $E$ and $p$ are determined uniquely up to isomorphism, and $\beth_W$ is defined as the fibre over the greatest element of $W^+$.

If all this seems rather familiar, it should! I gave a precisely analogous characterization of $\aleph_W$ rather than $\beth_W$ last time, with $p^{-1}(w) \gt p^{-1}(v)$ in place of $p^{-1}(w) \geq 2^{p^{-1}(v)}$.

Generally, if we write $Y \gg X$ to mean $Y \geq 2^X$, then the difference between the alephs and the beths is the difference between $\gt$ and $\gg$. Since $Y \gt X$ if and only if $Y \geq X^+$, this is another way of expressing the thought that the alephs are to the beths as $(\ )^+$ is to $2^{(\ )}$.

With this in mind, it’s easy to see that

$$\aleph_W \leq \beth_W$$

for all well-ordered sets $W$. More exactly, if $\beth_W$ exists then so does $\aleph_W$ and the inequality is true. If the generalized continuum hypothesis holds ($X^+ = 2^X$ for all infinite sets $X$) then the alephs and the beths are the same, but of course it needn’t hold.

Let’s now consider the existence of all beths, rather than individual ones. In other words, let’s think about the possible additional axiom:

$\beth_W$ exists for every well-ordered set $W$.

There’s an equivalent way of saying this that’s not inductive and doesn’t mention order either:

For all sets $I$, there exists a function $p: E \to I$ into $I$ such that for all distinct $i, j \in I$, either $2^{p^{-1}(i)} \leq p^{-1}(j)$ or $2^{p^{-1}(j)} \leq p^{-1}(i)$.

Again, this is an analogue of something I already said for the alephs, but with the relation $2^X \leq Y$ in place of $X \lt Y$.

As David Roberts pointed out in a comment in the context of the alephs, proving that this condition is equivalent to the existence of all beths isn’t completely trivial. The more tricky direction is to show that if this condition holds then all beths exist. For example, suppose you want to show that $\beth_\omega$ exists. It’s not enough to take $I$ to be the underlying set $\mathbb{N}$ of $\omega$, since the fibres could all be finite. You have to use an uncountable $I$. I don’t want to give the impression that the proof is hard — it’s not! — but I’m going to leave it to your imagination.

Let’s come back now to $\beth_\omega$. We saw that, if it exists, it’s the supremum of

$$\beth_0 = \mathbb{N},\ \beth_1 = 2^{\mathbb{N}},\ \beth_2 = 2^{2^{\mathbb{N}}}, \ldots.$$

But also, $\beth_\omega$ exists if and only if the coproduct

$$\mathbb{N} + 2^\mathbb{N} + 2^{2^\mathbb{N}} + \cdots$$

exists, and in that case, $\beth_\omega$ is this coproduct. The supremum is the same as the sum!

This becomes clear if you stare at this picture for long enough:

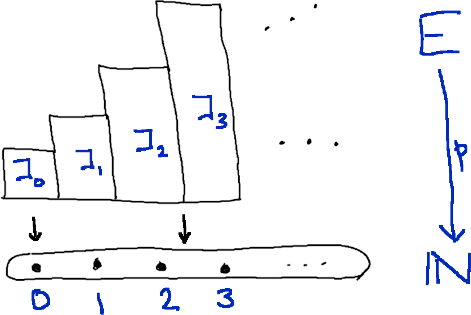
Got it? Let me say it in boring old words. Suppose that $\beth_\omega$ exists. Then the set $E$ shown can be constructed as a subset of $\mathbb{N} \times \beth_\omega$. And in fact, $\mathbb{N} \times \beth_\omega \cong \beth_\omega$, since $\mathbb{N} \leq \beth_\omega$. Hence the coproduct exists and is $\leq \beth_\omega$. Conversely, suppose that the coproduct exists; call it $S$. Then $S$ is certainly an upper bound of $\beth_0, \beth_1, \ldots$, so these sets have a least upper bound and it’s $\leq S$. Hence $\beth_\omega$ exists and is $\leq S$. That proves that the supremum is the same as the sum, and it shows that the total space $E$ in the diagram is exactly $\beth_\omega$.

Everything I’ve just said about $\omega$ is equally true for every limit well-ordered set $W$:

$$\beth_W = \sup_{V \prec W} \beth_V = \sum_{V \prec W} \beth_V.$$

And the argument is the same too. The step “$\mathbb{N} \leq \beth_\omega$” in the case $W = \omega$ gets replaced by the general fact that $U(W) \leq \beth_W$, where $U$ means underlying set. This follows from the chain of inequalities

$$U(W) \leq \aleph_W \leq \beth_W,$$

both of which I mentioned before.

In fact, we met $\beth_\omega$ before in Part 2, although I only mentioned its name in passing. It is the smallest uncountable strong limit. More exactly, in a model of ETCS, $\beth_\omega$ exists if and only if an uncountable strong limit exists, and in that case the smallest uncountable strong limit is $\beth_\omega$.

Why is $\beth_\omega$ a strong limit? You should be able to persuade yourself that if a well-ordered set $W$ is a limit then the set $\beth_W$ is a strong limit (recalling what this means: if $X \lt \beth_W$ then $2^X \lt \beth_W$). In particular, the well-ordered set $\omega$ is a limit, so the set $\beth_\omega$ is a strong limit.

Since uncountable strong limits are not guaranteed to exist in a model of ETCS, and $\beth_\omega$ is an uncountable strong limit, we can deduce:

It is consistent with ETCS that $\beth_\omega$ does not exist.

But let me prove this directly anyway, since it’s so easy. Take a model of ETCS. If $\beth_\omega$ does not exist in it, we’re done. If it does, call a set “small” if it is $\lt \beth_\omega$. Since $\beth_\omega$ is a strong limit, the small sets are a model of ETCS in which $\beth_\omega$ does not exist. That’s it!

The axiom “all beths exist” is quite useful. Here’s an example. Suppose we start with a vector space $V$, and we want to form the colimit in $\mathbf{Vect}$ of the sequence

$$V \to V^{\ast\ast} \to V^{\ast\ast\ast\ast} \to \cdots,$$

where each map is the canonical embedding of a space into its double dual. What do we need to add to ETCS in order to be sure that this colimit exists (or, indeed, that this diagram is even mentionable)?

A little thought reveals that we’re OK as long as for any set $X$, the sets

$$X, 2^X, 2^{2^X}, \ldots$$

have a supremum. (This sufficient condition is necessary too, as you can see by thinking about vector spaces over $\mathbb{F}_2$.) Now assume that all beths exist. We can find some beth at least as big as $X$: for example, if we take a well order $W$ with underlying set $X$, then $\beth_W \geq U(W) \cong X$. And then $\beth_{W + \omega}$ is a supremum for this sequence of sets. (I’ll explain the meaning of $+$ in a moment; it’s what’s usually called “ordinal sum”.)

So, “all beths exist” guarantees the existence of such colimits.

The existence of all beths is a stronger condition than the existence of uncountable strong limits — stronger, even, than the existence of unboundedly many strong limits. First let’s see why one implies the other:

All beths exist $\implies$ unboundedly many strong limits.

Suppose we have a model of ETCS in which all beths exist. Take any set $X$. Our task is to find some strong limit $\geq X$, and we might as well assume that $X$ is infinite. Now, there’s some initial well order $W$ with underlying set $X$, and then

$$X \cong U(W) \leq \beth_W.$$

So $X \leq \beth_W$. Since $W$ is an initial well order (i.e. $\preceq$-least of its cardinality) and infinite, it can’t be a successor. So $W$ is a limit, which implies that $\beth_W$ is a strong limit.

(Again, this might seem familiar, because I gave the same argument last time for alephs and weak limits rather than beths and strong limits.)

“All beths exist” is strictly stronger than “there are unboundedly many strong limits”. That is:

It is consistent with ETCS + (there are unboundedly many strong limits) that not all beths exist.

It seems to be a feature of categorical set theory that ordinal arithmetic plays a less prominent role than in more traditional treatments. Nevertheless, we’ll need a little bit to prove this result.

The basic definitions are these. Given ordered sets $V$ and $W$, we can form:

• Their sum $V + W$. This is the disjoint union of $V$ and $W$, with the original orderings on each of the parts $V$ and $W$, and with $v \lt w$ whenever $v \in V$ and $w \in W$.

• Their reverse lexicographic product $V \cdot W$. Its underlying set is the cartesian product $V \times W$, and we define $(v, w) \lt (v', w')$ if either $w \lt w'$ or ($w = w'$ and $v \lt v'$).

If $V$ and $W$ are well-ordered then so are $V + W$ and $V \cdot W$. We’ll be talking about $\omega^2 = \omega \cdot \omega$ and $\omega \cdot n = \omega + \cdots + \omega$ for natural numbers $n$.

Now take a model of ETCS with unboundedly many strong limits. We want to build a model with unboundedly many strong limits in which not all beths exist.

If $\beth_{\omega^2}$ does not exist in this model, we’re done.

Now assuming that $\beth_{\omega^2}$ does exist in our model, call a set “small” if it’s $\lt \beth_{\omega^2}$. Since the well-ordered set $\omega^2$ is a limit, the set $\beth_{\omega^2}$ is a strong limit, so the small sets are a model of ETCS in which not all beths exist. We have

$$\omega^2 = \sup_{n \in \mathbb{N}} \omega \cdot n,$$

which implies that

$$\beth_{\omega^2} = \sup_{n \in \mathbb{N}} \beth_{\omega \cdot n}.$$

Hence every small set is $\leq \beth_{\omega \cdot n}$ for some natural number $n$. And since the well-ordered set $\omega \cdot n$ is a limit, the set $\beth_{\omega \cdot n}$ is a strong limit, giving us the conclusion we wanted: every small set is $\leq$ some small set that’s a strong limit.

Last time, I promised to give you the proof of the analogous statement for alephs and weak limits:

It is consistent with ETCS + (there are unboundedly many weak limits) that not all alephs exist.

But now that I think about it harder, I’m not sure I can fulfil that promise. So let me show you the argument I had in mind and ask for your help in filling the gap it contains.

It goes like this. Take a model of ETCS with unboundedly many weak limits. I think we can assume that our model satisfies the generalized continuum hypothesis. In that case, weak and strong limits are the same, and alephs and beths are the same, so the statement to be proved follows from the one I just did prove. And that’s it.

The question is whether it’s consistent with ETCS and the existence of unboundedly many weak limits that the generalized continuum hypothesis (GCH) holds. Certainly GCH is consistent with ETCS alone. I imagine that if I went through the proof of this theorem, I’d be able to adapt it so that the axiom “there are unboundedly many weak limits” came along for the ride with the rest of the ETCS axioms. But I don’t know this. Do you?

Next time

We’ve repeatedly used the inequality $U(W) \leq \beth_W$ for well-ordered sets $W$. At first, it may seem implausible that equality could ever hold, given how vastly bigger $\beth_W$ is than $W$ for small values of $W$. But it can! Or at least, requiring the existence of some $W$ such that $U(W) \cong \beth_W$ is a sensible “large set” axiom (and already implied by ZFC). Such $W$s are called beth fixed points, and they’re our subject for next time.