An M5-Brane Model
Posted by John Baez
When you try to quantize 10-dimensional supergravity theories, you are led to some theories involving strings. These are fairly well understood, because the worldsheet of a string is 2-dimensional, so string theories can be studied using 2-dimensional conformal quantum field theories, which are mathematically tractable.
When you try to quantize 11-dimensional supergravity, you are led to a theory involving 2-branes and 5-branes. People call it M-theory, because while it seems to have magical properties, our understanding of it is still murky — because it involves these higher-dimensional membranes. They have 3- and 6-dimensional worldsheets, respectively. So, precisely formulating M-theory seems to require understanding certain quantum field theories in 3 and 6 dimensions. These are bound to be tougher than 2d quantum field theories… tougher to make mathematically rigorous, for example… but even worse, until recently people didn’t know what either of these theories were!
In 2008, Aharony, Bergman, Jafferis and Maldacena figured out the 3-dimensional theory: it’s a supersymmetric Chern–Simons theory coupled to matter in a way that makes it no longer a topological quantum field theory, but still conformally invariant. It’s now called the ABJM theory. This discovery led to the ‘M2-brane mini-revolution’, as various puzzles about M-theory got solved.
The 6-dimensional theory has been much more elusive. It’s called the (0,2) theory. It should be a 6-dimensional conformal quantum field theory. But its curious properties got people thinking that it couldn’t arise from any Lagrangian — a serious roadblock, given how physicists normally like to study quantum field theories. But people have continued avidly seeking it, and not just for its role in a potential ‘theory of everything’. Witten and others have shown that if it existed, it would shed new light on Khovanov duality and geometric Langlands correspondence! The best introduction is here:
- Edward Witten, Geometric Langlands from six dimensions, 2009.
In a recent interview with Quanta magazine, Witten called this elusive 6-dimensional theory “the pinnacle”:
Q: I’ve heard about the mysterious (2,0) theory, a quantum field theory describing particles in six dimensions, which is dual to M-theory describing strings and gravity in seven-dimensional AdS space. Does this (2,0) theory play an important role in the web of dualities?
A: Yes, that’s the pinnacle. In terms of conventional quantum field theory without gravity, there is nothing quite like it above six dimensions. From the (2,0) theory’s existence and main properties, you can deduce an incredible amount about what happens in lower dimensions. An awful lot of important dualities in four and fewer dimensions follow from this six-dimensional theory and its properties. However, whereas what we know about quantum field theory is normally from quantizing a classical field theory, there’s no reasonable classical starting point of the (2,0) theory. The (2,0) theory has properties [such as combinations of symmetries] that sound impossible when you first hear about them. So you can ask why dualities exist, but you can also ask why is there a 6-D theory with such and such properties? This seems to me a more fundamental restatement.
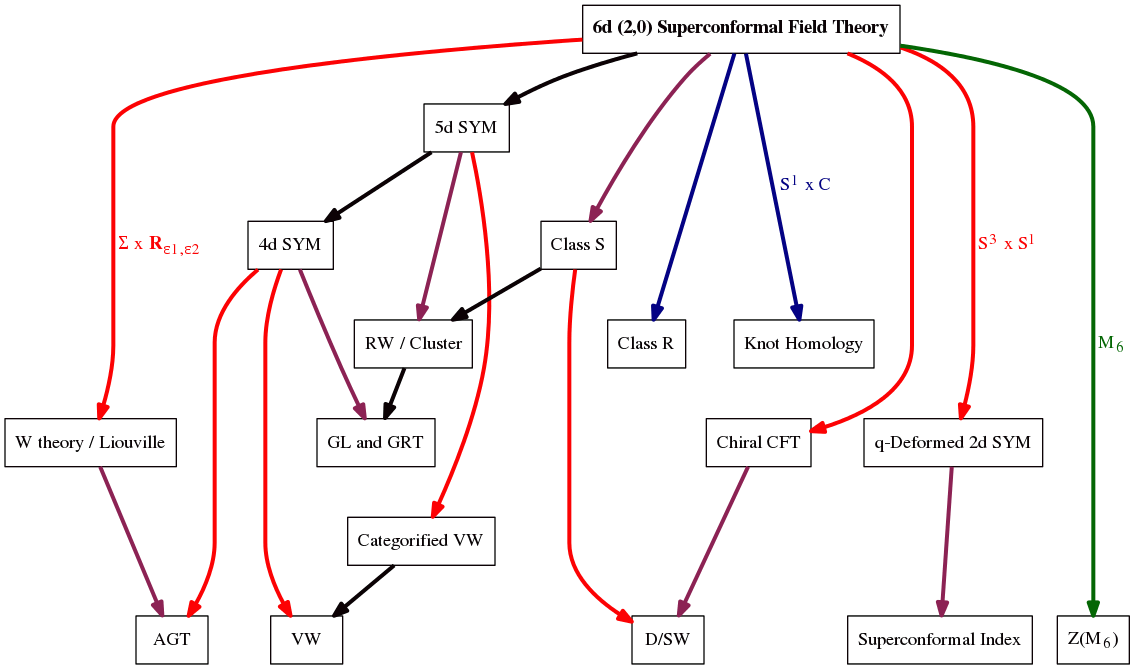
Indeed, it sits atop a terrifying network of field theories in various lower dimensions:
Now, maybe, maybe this theory has been found:
- Christian Saemann, Lennart Schmidt, An M5-brane model.
As Urs cautiously and wisely wrote:
If this holds water, it will be big.
Here’s the abstract:
Abstract. We present an action for a six-dimensional superconformal field theory containing a non-abelian tensor multiplet. All of the ingredients of this action have been available in the literature. We bring these pieces together by choosing the string Lie 2-algebra as a gauge structure, which we motivated in previous work. The kinematical data contains a connection on a categorified principal bundle, which is the appropriate mathematical description of the parallel transport of self-dual strings. Our action can be written down for each of the simply laced Dynkin diagrams, and each case reduces to a four-dimensional supersymmetric Yang-Mills theory with corresponding gauge Lie algebra. Our action also reduces nicely to an M2-brane model which is a deformation of the ABJM model.
My own interest in this is purely self-centered. I hope this theory holds water — I hope it continues to pass various tests it needs to pass to be the elusive (0,2) theory — because it uses ideas from higher gauge theory, and in particular the string Lie 2-algebra!
This is a ‘categorified Lie algebra’ that one can construct starting from any Lie algebra with an invariant inner product. It was first found (though not under this name) by Alissa Crans, who was then working on her thesis with me:
- Alissa Crans, Lie 2-Algebras, Ph.D. thesis, U.C. Riverside, 2004.
The idea was published here:
- John Baez and Alissa Crans, Higher-dimensional algebra VI: Lie 2-algebras, TAC 12 (2004), 492–528.
In 2005, together with Danny Stevenson and Urs Schreiber, we connected the string Lie 2-algebra to central extensions of loop groups and the ‘string group’:
- John C. Baez, Alissa S. Crans, Danny Stevenson, Urs Schreiber, From loop groups to 2-groups, Homotopy, Homology and Applications 9 (2007), 101–135.
though our paper was published only after a struggle. Subsequently Urs worked out a much better understanding of how Lie -algebras appear in higher gauge theory and string theory. In 2012, together with Domenico Fiorenza, Hisham Sati, he began working out how string Lie 2-algebras are related to the 5-branes in M-theory:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Multiple M5-branes, string 2-connections, and 7d nonabelian Chern-Simons theory, ATMP 18 (2014), 229–321.
They focused on the 7-dimensional Chern–Simons theory which should be connected to the elusive 6-dimensional (0,2) theory via the AdS/CFT correspondence. The new work by Saemann and Schmidt goes further by making an explicit proposal for the Lagrangian of the 6-dimensional theory.
For more details, read Urs’ blog article on G+.
All this leaves me feeling excited but also bemused. When I started thinking about 2-groups and Lie 2-algebras, I knew right away that they should be related to the parallel transport of 1-dimensional objects — that is, strings. But not being especially interested in string theory, I had no inkling of how, exactly, the Lie 2-algebras that Alissa Crans and I discovered might play a role in that subject. That began becoming clear in our paper with Danny and Urs. But then I left the subject, moving on to questions that better fit my real interests.
From tiny seeds grow great oaks. Should have stuck with the string Lie 2-algebra and helped it grow? Probably not. But sometimes I wish I had.

Re: An M5-Brane Model
What did you have to fight about to get that last paper published?