The n-Category Café

First, I should remind you about what we did in Division Algebras and Supersymmetry II: we used the normed division algebras to construct Lie 2-superalgebra extensions to the Poincaré superalgebra in spacetimes of the superstring dimensions: 3, 4, 6 and 10.

Wow! That’s already a lot to explain, but fortunately, John Baez already explained a lot of it here before:

• Division Algebras and Supersymmetry II, the $n$-Category Café.

So let me quote the inimitable John Baez:

The groups that physicists like all have Lie algebras. Lie algebras show up in particle physics because they describe how particles transform as they move around. But recently people have discovered gadgets called Lie 2-algebras, which do the same job for strings. And Lie 3-algebras, which do the same job for 2-dimensional membranes, usually called ‘2-branes’. And so on!

In fact, a Lie $n$-algebra is actually a kind of hybrid structure: a blend of a Lie algebra and an $n$-category.

But if you’re a practical sort of person, you may want to build a Lie $n$-algebra starting from some stuff you can easily get your hands on. The simplest way is to start with a Lie algebra and a gizmo called an $(n+1)$-cocycle: some sort of function satisfying some equation called a ‘cocycle condition’. From this, you can get a Lie $n$-algebra that includes your original Lie algebra.

Cutting to the chase, this is exactly what do: we build a Lie 2-superalgebra extending the Poincaré superalgebra, using a 3-cocycle that exists exactly when the dimension of spacetime is 3, 4, 6 and 10. What is the Poincaré superalgebra, you ask? Its the ‘super version’ of the Poincaré algebra, of course! Quoting John one more time:

You see, special relativity says we live in Minkowski spacetime. The group of symmetries of Minkowski spacetime is called the Poincaré group. This has a Lie algebra: the Poincaré algebra. And there’s a supersymmetric analogue of all this, starting from ‘super-Minkowski spacetime’. Super-Minkowski spacetime unifies vectors and spinors in a nice way. And the supergroup of symmetries of super-Minkowski spacetime has a Lie superalgebra, called the Poincaré superalgebra.

Super!

So it isn’t too hard to believe that the Poincaré superalgebra is really important if you want to talk about supersymmetric theories of physics, like the superstring. Moreover, this 3-cocycle on the Poincaré superalgebra helps to make superstring theory tick: physicists explain how it is necessary for the superstring to have a kind of local supersymmetry called ‘Siegel symmetry’. I don’t really understand Siegel symmetry or why it’s needed, but I suspect that because it is local and super, it plays a big role in connecting the superstring to another famous theory with local supersymmetry: namely, supergravity.

The upshot is that we get a Lie 2-superalgebra extending Poincaré superalgebra whenever we can also have the superstring. Hence, we call this the superstring Lie 2-algebra, $\mathfrak{superstring}$. And thanks to the work of super smart people like Hisham Sati, Urs Schreiber and Jim Stasheff on higher gauge theory:

• Hisham Sati, Urs Schreiber and Jim Stasheff, $L_\infty$-algebra connections and applications to String- and Chern–Simons $n$-transport

we know this is no mere coincidence, but is turning out to be an important part of string theory.

I hope all of this convinces you that $\mathfrak{superstring}$ is important. But there’s something missing from this story: for gauge theory we have Lie groups and Lie algebras. For higher gauge theory, we have Lie 2-groups and Lie 2-algebras, and for higher gauge theory with supersymmetry, we have Lie 2-supergroups and Lie 2-superalgebras. What is the 2-supergroup that corresponds to the Lie 2-superalgebra $\mathfrak{superstring}$?

In my new paper, I’ll tell you! And right now, I’ll tell you how I got the answer. Remember how we got our hands on $\mathfrak{superstring}$ using a 3-cocycle? Well, one can use 3-cocycles of a different sort to get our hands on 2-groups. And because this is the $n$-Category Café, you probably won’t mind if I remind you how this works.

2-groups from 3-cocycles

Remember, a 2-group is a category $\mathcal{G}$ with invertible morphisms equipped with a multiplication functor:

$$m \colon \mathcal{G} \times \mathcal{G} \to \mathcal{G}$$

satisfying the group laws up to natural isomorphism. For instance, rather than being associative, we have an associator:

$$a_{g_1,g_2,g_3} \colon (g_1 g_2)g_3 \to g_1(g_2g_3)$$

for any trio of objects $g_1$, $g_2$ and $g_3$ in $\mathcal{G}$. These natural isomorphisms then satisfy some laws of their own. For instance, the associator satisfies the pentagon identity, which says the following pentagon commutes:

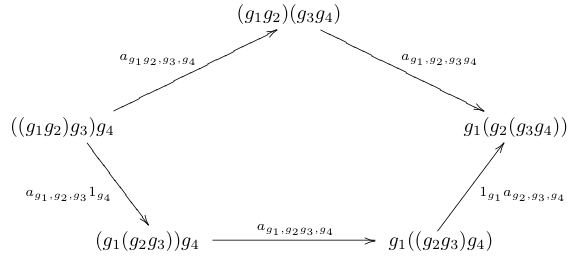
Suffice to say, every 2-group has a lot of data (objects, morphisms, natural isomorphisms) subject to several axioms. Luckily, thanks to a theorem of Joyal and Street, we can distill all this down to only four things:

• a group $G$,
• an abelian group $H$,
• an action of $G$ on $H$ by automorphism,
• an $H$-valued 3-cocycle $a$ on $G$.

This last item, the 3-cocycle, is just some function:

$$a \colon G^3 \to H$$

satisfying an equation called a ‘cocycle condition’. What is this equation? Well, it’s secretly just the pentagon identity! In fact, Joyal and Street proved that every 2-group is equivalent to a 2-group which has:

• An object $g$ for each element of the group $G$.
• On each object $g$, an automorphism $h \colon g \to g$ for each element $h$ of the abelian group $H$, and no morphisms between different objects. Composition of morphisms is addition in $H$.
• Multiplication of objects is multiplication in $G$.
• Multiplication of morphisms: $$h \colon g \to g , \quad h' \colon g' \to g'$$ is addition twisted by the action of $G$: $$h + g h' \colon g g' \to g g' .$$
• The associator: $$a_{g_1,g_2,g_3} \colon (g_1 g_2)g_3 \to g_1(g_2g_3)$$ given by the 3-cocycle $a \colon G^3 \to H$.

This works out to be a 2-group, because $a$ satisfies the pentagon identity if and only if it is a 3-cocycle in the more mundane sense of group cohomology. Note that even though multplication is associative ($G$ is a group, after all), we can still have nontrivial associators. Weird! In fact, we can think of $a$ as kind of obstruction to making a 2-group strictly associative, as spelled out in HDA5.

For this story, however, what matters is that:

• A 3-cocycle on a group $G$ gives a 2-group extending $G$.

And this is an example of a broad pattern:

• A 3-cocycle on a Lie group $G$ gives a Lie 2-group extending $G$.
• A 3-cocycle on a supergroup $G$ gives a 2-supergroup extending $G$.

In fact, we saw this pattern with Lie algebras, too:

• A 3-cocycle on a Lie algebra $\mathfrak{g}$ gives a Lie 2-algebra extending $\mathfrak{g}$.
• A 3-cocycle on a Lie superalgebra $\mathfrak{g}$ gives a Lie 2-superalgebra extending $\mathfrak{g}$.

After all, this was how we got our hands on the Lie 2-superalgebra, $\mathfrak{superstring}$, which extends the Poincaré superalgebra.

Now, of course, I haven’t defined ‘2-supergroups’, or for that matter Lie 2-algebras. Right now, the exact definition is not important. What’s important is that 3-cocycles give examples. Because that’s how we are going to integrate $\mathfrak{superstring}$: we will find a 3-cocycle on the Poincaré supergroup which integrates the 3-cocycle used to define $\mathfrak{superstring}$.

Integrating cocycles

Let me finish off with a taste of how this integration works, but made easier because it’s not super: I’ll tell you how to integrate a 3-cocycle on a Lie algebra, $\mathfrak{g}$, to a 3-cocycle on the corresponding Lie group, $G$. Of course, that means I’ll have to tell you what each of those things is, so let me give you two definitions that suit my purpose:

• A 3-cocycle on the Lie algebra $\mathfrak{g}$ is a closed, left-invariant 3-form on the Lie group $G$.

Sneaky, eh? I’m already working with something defined on the Lie group. But I’m not cheating, because we can always take a structure defined on the Lie algebra and left translate it to get a structure defined on the group.

• A 3-cocycle on the Lie group $G$ is a smooth function $a \colon G^3 \to \mathbb{R}$ satisfying the equation: $$a(g_2, g_3, g_4) - a(g_1 g_2, g_3, g_4) + a(g_1, g_2 g_3, g_4) - a(g_1, g_2, g_3 g_4) + a(g_1, g_2, g_3) = 0 .$$

At this point, you’re probably wondering where that silly equation came from. Remember the pentagon identity:

where composition is just addition, and you’re not far from the equation above. But I have carefully arranged the terms hopefully to make my punchline, a surprise application of Stokes’ theorem, as easy as possible.

So, given a Lie algebra 3-cocycle $\omega$ (a closed, left-invariant 3-form), how are we going to get a Lie group 3-cocycle? Just integrate our 3-form over a 3-simplex:

$$\displaystyle a(g_1, g_2, g_3) = \int_{[1,g_1,g_1g_2,g_1g_2g_3]} \omega .$$

Here $[1,g_1,g_1g_2,g_1g_2g_3]$ is some standard way of filling out a 3-simplex in $G$ with the given vertices. Choose this ‘standard filling’ carefully, and you can also make sure it has the virtue of being left-invariant:

$$g[g_0, \ldots, g_p] = [g g_0, \ldots, g g_p]$$

so let’s assume that here. Constructing these left-invariant simplices is the biggest challenge of the paper, and requires some technical assumptions about $G$—namely, that the exponential map:

$$\exp \colon \mathfrak{g} \to G$$

be a diffeomorphism. When this happens, $G$ is called exponential.

Once this simplex is constructed, however, we’re home free. I’ll leave the last bit of work, checking that $a$ is a 3-cocycle, to you. I can’t resist giving a big hint, however: use Stokes’ theorem!