Mixed Volume

August 26, 2011

Posted by Tom Leinster

$MathML-enabled post (click for more details).$

Take $2$ convex bodies in $\mathbb{R}^2$ , or $3$ convex bodies in $\mathbb{R}^3$ , or, more generally, $n$ convex bodies in $\mathbb{R}^n$ . Mixed volume assigns to each such family a single real number.

The mixed volume of convex bodies $A_1, \ldots, A_n$ is written as $V(A_1, \ldots, A_n) \in \mathbb{R}$ , and it’s uniquely characterized by the following three properties:

Volume: $V(A, \ldots, A) = Vol(A)$ , for any convex body $A$
Symmetry: $V$ is symmetric in its arguments
Multiadditivity: $V(A_1 + \tilde{A}_1, A_2, \ldots, A_n)$ equals $V(A_1, A_2, \ldots, A_n) + V(\tilde{A}_1, A_2, \ldots, A_n)$ for any convex bodies $A_i$ and $\tilde{A}_1$ , where $+$ denotes Minkowski sum.

This looks rather like the characterization of determinant: $det$ is unique satisfying $det(I) = 1$ , antisymmetry, and multilinearity. One difference is that we have symmetry rather than antisymmetry. But a much bigger difference is that where determinant assigns a number to $n$ vectors in $\mathbb{R}^n$ , mixed volume assigns a number to $n$ convex bodies in $\mathbb{R}^n$ .

But maybe you don’t find the unique characterization satisfying. What is mixed volume?

$MathML-enabled post (click for more details).$

First I should be precise about what I mean by ‘convex body’. I simply mean a compact, convex, nonempty subset of $\mathbb{R}^n$ . (Often people include the condition that the interior is nonempty, but I’m not requiring that.) You might raise an eyebrow at the word ‘nonempty’, but it really does matter.

In a moment I’ll give you lots of examples of mixed volume. Later on, I’ll give you the definition, and I’ll also list some of the other properties that it satisfies (apart from the three that characterize it uniquely). But the examples will be easier to understand if I tell you one of those properties right now:

4. Translation-invariance in each coordinate: $V(x + A_1, A_2, \ldots, A_n) = V(A_1, A_2, \ldots, A_n)$ for any convex bodies $A_i$ and any $x \in \mathbb{R}^n$ .

Since $V$ is symmetric, this implies that

$V(x_1 + A_1, \ldots, x_n + A_n) = V(A_1, \ldots, A_n).$

In other words, sliding the bodies around doesn’t change the mixed volume. (Changing their orientations usually does, as we’ll see.) Knowing this helps us to speak more freely. If, say, $n = 2$ , then I can say ‘let $A_1$ be a $3 \times 4$ rectangle with edges parallel to the coordinate axes’ — I don’t need to say where in the plane it lives.

Examples of mixed volume

Example I’ve already mentioned that $V(A, \ldots, A) = A$ for any convex body $A$ . Now suppose that our $n$ convex bodies are not necessarily equal, but are all scalings of one another. Given a convex body $B$ and scalars $t_1, \ldots, t_n \gt 0$ , we have

$V(t_1 B, \ldots, t_n B) = t_1 \cdots t_n Vol(B)$

where $t_i B$ means $\{ t_i b | b \in B\}$ . To put it another way: if $A_1, \ldots, A_n$ are all scalings of one another then

$V(A_1, \ldots, A_n) = geometric mean of Vol(A_1), \ldots, Vol(A_n).$

Example The previous example is misleading, because it doesn’t reveal that in general, mixed volume depends on how the convex bodies interact with one another. But a simple example with $n = 2$ will show this. Let $A$ be an $a \times b$ rectangle and $B$ a $c \times d$ rectangle, both with their edges parallel to the coordinate axes. Then

$V(A, B) = \frac{1}{2}(a d + b c).$

Here’s a picture:

The mixed volume — which for $n = 2$ could be called ‘mixed area’ — is not derived from the areas of $A$ and $B$ , shown in grey. Instead, it’s the (arithmetic) mean of the areas of the two red rectangles.

The formula for $V(A, B)$ looks a bit like the determinant formula $a d - b c$ …. We’ll come back to this.

Example Let’s generalize the previous example to higher dimensions. Rectangles, then, will become cuboids. Previously we established that the word ‘cuboid’ is known to British schoolchildren and comedians, but not American math professors (I’m teasing, John). I believe American English uses some quaint term such as ‘orthogonal parallelepiped’. Anyway: let $n$ be any natural number, let $(a_{i j})$ be an $n \times n$ matrix of nonnegative reals, and for $i = 1, \ldots, n$ , let

$A_i = [0, a_{i 1}] \times \cdots \times [0, a_{i n}] \subseteq \mathbb{R}^n.$

(Or you could take $A_i$ to be a translate of this; it doesn’t matter.) Then

$V(A_1, \ldots, A_n) = \frac{1}{n!} \sum_{\sigma \in S_n} a_{1, \sigma(1)} \cdots a_{n, \sigma(n)}.$

Again, this can usefully be compared to the determinant formula

$det((a_{i j})) = \sum_{\sigma \in S_n} sgn(\sigma) a_{1, \sigma(1)} \cdots a_{n, \sigma(n)}.$

Apart from the constant factor, the only difference is in the signs. This corresponds to mixed volume being symmetric and determinant being antisymmetric.

I said before that whereas determinant assigns a number to any $n$ vectors in $\mathbb{R}^n$ , mixed volume assigns a number to any $n$ convex bodies in $\mathbb{R}^n$ . Actually, every vector gives rise to a convex body: it’s the axis-parallel cuboid whose long diagonal is $v$ . For example, the vector $\mathbf{a}_i = (a_{i 1}, \ldots, a_{i n})$ gives rise in this way to the cuboid $A_i$ . In the last paragraph, we compared the determinant of the $n$ vectors $\mathbf{a}_1, \ldots, \mathbf{a}_n$ with the mixed volume of the $n$ convex bodies $A_1, \ldots, A_n$ they give rise to.

Minkowski’s theorem

I still haven’t told you the definition of mixed volume. One reason why not is that in order to even state the definition, we first need to know the following theorem of Minkowski.

Theorem (Minkowski) Let $k$ and $n$ be natural numbers. Fix convex bodies $A_1, \ldots, A_k$ in $\mathbb{R}^n$ . Then the function

$(t_1, \ldots, t_k) \mapsto Vol(t_1 A_1 + \cdots + t_k A_k)$

( $t_i \geq 0$ ) is a polynomial, homogeneous of degree $n$ .

If you understand Minkowski’s theorem, you understand mixed volume. So I’ll do my best to explain it.

The first thing to notice is that whereas we had been discussing $n$ bodies in $n$ -dimensional space, we’re now discussing $k$ bodies in $n$ -dimensional space. Of course, you can take $k = n$ , but it’s probably easier to understand Minkowski’s theorem if we treat it at its natural level of generality.

Now let’s look for the first nontrivial case.

For $k = 0$ , the theorem is trivial.

For $k = 1$ , it says that given any convex body $A$ in $\mathbb{R}^n$ , the function

$t \mapsto Vol(t A)$

( $t \geq 0$ ) is a polynomial in $t$ , homogeneous of degree $n$ . That’s true, and doesn’t even use convexity: the polynomial is $Vol(A) \cdot t^n$ .

It’s when $k = 2$ that things start to get interesting. The statement is that for convex bodies $A, B \subseteq \mathbb{R}^n$ , the function

$(s, t) \mapsto Vol(s A + t B)$

is a homogeneous polynomial of degree $n$ . Because $Vol$ itself is homogeneous of degree $n$ , we might as well fix $s$ to be $1$ . Then Minkowski is telling us that

$t \mapsto Vol(A + t B)$

is a polynomial of degree $\leq n$ .

Why is that so? The picture below shows an example with $n = 2$ . Here $A$ is the blue quadrilateral, $t B$ is any one of the green egg shapes, and $A + t B$ is the whole thing, including the grey parts. (The four copies of $t B$ that I’ve chosen to draw are $a + t B$ for the four vertices $a$ of $A$ .)

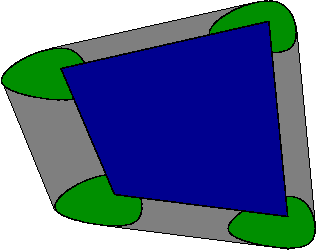
Minkowski sum

Minkowski’s theorem implies that the area of the whole thing is a (possibly degenerate) quadratic in $t$ .

So let’s try to understand some special cases. I’m sticking with $k = 2$ : that is, I’m trying to explain why $Vol(A + t B)$ is a polynomial in $t$ of degree at most $n$ , whenever $A$ and $B$ are convex bodies in $\mathbb{R}^n$ .

Example Take $B$ to be a singleton $\{b\}$ . Then $A + t B = A + t b$ , a translate of $A$ . Hence $Vol(A + t B) = Vol(A)$ for all $t$ . This is certainly a polynomial in $t$ of degree $\leq n$ .

Example Take $B = A$ . Then

$Vol(A + t B) = Vol((1 + t)A) = Vol(A)\cdot(1 + t)^n,$

which is indeed a polynomial of degree $\leq n$ .

Example Choose a point $b \in \mathbb{R}^n$ and take $B$ to be the straight line segment $[0, b]$ from $0$ to $b$ . Then

$Vol(A + t B) = Vol(A + [0, t b]).$

Here’s a picture with $n = 2$ and with $b$ somewhere on the positive $x$ -axis:

As before, $A$ is in blue. It’s clear that the area of the grey part is proportional to the horizontal distance over which $A$ has been smeared out — that is, proportional to $t$ . This gives

$Vol(A + t B) = Vol(A) + c t$

for some constant $c$ , and again, this is a polynomial in $t$ of degree $\leq n$ .

Example Take $B$ to be the unit ball. Then $A + t B$ is the closed $t$ -neighbourhood of $A$ , that is, the set of all points $x$ such that $inf_{a \in A} d(x, a) \leq t$ . And there’s a famous theorem giving the volume of the $t$ -neighbourhood: Steiner’s theorem.

By law, every explanation of Steiner’s theorem must contain the following diagram:

Staring at this picture should reveal to you the following truth: for convex bodies $A$ in $\mathbb{R}^2$ ,

$Vol(A + t B) = Vol(A) + perimeter(A)\cdot t + \pi t^2.$

This is a polynomial in $t$ of degree $2$ . There’s a similar formula in higher dimensions. The coefficients are, up to a constant factor, the intrinsic volumes of $A$ .

That’s enough explanation; it’s time to give you the definition.

The definition of mixed volume

Take $n$ convex bodies in $\mathbb{R}^n$ , say $A_1, \ldots, A_n$ . Minkowski’s theorem states that

$Vol(t_1 A_1 + \cdots + t_n A_n)$

is a polynomial in $t_1, \ldots, t_n \geq 0$ , homogeneous of degree $n$ . The mixed volume $V(A_1, \ldots, A_n)$ is the coefficient of $t_1 t_2 \cdots t_n$ in this polynomial, divided by $n!$ .

This definition is apt to look mysterious. For a start, why this particular coefficient? It’s because, as it turns out, mixed volume tells you all the coefficients.

The precise statement is as follows. Take any natural numbers $k$ and $n$ , and any $k$ convex bodies $A_1, \ldots, A_k$ in $\mathbb{R}^n$ . Then

$Vol(t_1 A_1 + \cdots + t_k A_k) = \sum_{i_1, \ldots, i_n = 1}^k V(A_{i_1}, \ldots, A_{i_n}) t_{i_1} \cdots t_{i_n}.$

So if someone put an implant in your brain that enabled you to calculate any mixed volume, you’d also be able to calculate the Minkowski polynomial of any family of convex bodies.

Example Take $k = n = 2$ . Then this tells us that

$Vol(t_1 A_1 + t_2 A_2) = V(A_1, A_1) t_1^2 + 2V(A_1, A_2) t_1 t_2 + V(A_2, A_2) t_2^2.$

But $V(A_i, A_i) = Vol(A_i)$ , so what this essentially says is that

$Vol(A + t B) = Vol(A) + 2V(A, B) t + Vol(B) t^2.$

You can check this in some of the examples above.

Another way to express this equation is:

$Vol(t_1 A_1 + \cdots + t_k A_k) = \sum_{n_1 + \cdots + n_k = n} \binom{n}{n_1, \ldots, n_k} V(A_1^{n_1}, \ldots, A_k^{n_k}) t_1^{n_1} \cdots t_k^{n_k}.$

Here $\binom{n}{n_1, \ldots, n_k}$ is the multinomial coefficient $\frac{n!}{n_1! \cdots n_k!}$ , and by definition,

$V(A_1^{n_1}, \ldots, A_k^{n_k}) = V(A_1, \ldots, A_1, \ldots, A_k, \ldots, A_k)$

where each $A_i$ appears $n_i$ times. So, mixed volumes with repeated arguments are important. In this respect, mixed volume is unlike determinant: because of antisymmetry, determinants with repeated arguments are trivial.

The unique characterization

I began by stating that mixed volume is uniquely characterized by three properties: the volume property ( $V(A, \ldots, A) = Vol(A)$ ), symmetry, and multiadditivity. It’s easy to prove that when $n = 2$ , there’s at most one function $V$ satisfying the three properties. It’s a bit like the proof that in an inner product space, the norm determines the inner product. Indeed, if $V$ satisfies the properties then by multiadditivity we have

$V(A + B, A + B) = V(A, A) + V(A, B) + V(B, A) + V(B, B),$

and so by symmetry and the volume property,

$V(A, B) = \frac{1}{2}\Bigl\{Vol(A + B) - \bigl[Vol(A) + Vol(B)\bigr]\Bigr\}.$

(This is the same as the formula in the last example, rearranged and with $t = 1$ .) So mixed volume can be expressed in terms of ordinary volume and Minkowski sums.

You can do the same kind of thing in higher dimensions. When $n = 3$ , for instance, you get

$V(A, B, C) = \frac{1}{3!} \Bigl\{ V(A + B + C) - \bigl[V(A + B) + V(A + C) + V(B + C)\bigr] + \bigl[V(A) + V(B) + V(C)\bigr] \Bigr\}.$

The formula for general $n$ is now exactly as you’d guess.

That’s a very explicit formula for mixed volume, though it’s not clear that it gives much insight. By way of analogy, does the formula

$a b = \frac{1}{2}\bigl\{[a + b]^2 - [a^2 + b^2]\bigr\}$

give you a lot of insight into multiplication of real numbers? It’s probably important in some contexts, and it’s interesting that multiplication can be built out of addition, squaring and halving. But it’s not how most of us think about multiplication.

Further properties of mixed volume

In the absence of a single really compelling way to understand mixed volume, I’ve described several ways in which it can be half-understood. There’s the unique characterization by three properties, there’s the analogy with determinants, there are examples, there’s the definition in terms of the polynomial in Minkowski’s theorem, and there’s the formula we just met, giving mixed volume as a linear combination of ordinary volumes.

I’ll finish with another way of half-understanding it. It’s a long list of properties that mixed volume satisfies. For completeness, I’ll begin with the four that we’ve already seen.

Volume: $V(A, \ldots, A) = Vol(A)$
Symmetry: $V$ is symmetric in its arguments
Multiadditivity: $V(A_1 + \tilde{A}_1, A_2, \ldots, A_n) = V(A_1, A_2, \ldots, A_n) + V(\tilde{A}_1, A_2, \ldots, A_n)$
Translation-invariance in each coordinate: $V(x + A_1, A_2, \ldots, A_n) = V(A_1, A_2, \ldots, A_n)$
Isometry-invariance: $V(g A_1, \ldots, g A_n) = V(A_1, \ldots, A_n)$ for any $g$ in the isometry group of $\mathbb{R}^n$
Special linear invariance: $V(g A_1, \ldots, g A_n) = V(A_1, \ldots, A_n)$ for any $g \in SL(n, \mathbb{R})$
Scaling: $V(t A_1, A_2, \ldots, A_n) = t V(A_1, A_2, \ldots, A_n)$ for any $t \geq 0$
Singletons: $V(\{a\}, A_2, \ldots, A_n) = 0$
Monotonicity: $V(A_1, A_2, \ldots, A_n) \leq V(\tilde{A}_1, A_2, \ldots, A_n)$ whenever $A_1 \subseteq \tilde{A}_1$
Nonnegativity: $V(A_1, \ldots, A_n) \geq 0$
Continuity: $V$ is continuous with respect to the Hausdorff metric on convex bodies
Valuation in each coordinate: $V(A_1 \cup \tilde{A}_1, A_2, \ldots) = V(A_1, A_2, \ldots) + V(\tilde{A}_1, A_2, \ldots) - V(A_1 \cap \tilde{A}_1, A_2, \ldots)$ as long as $A_1 \cup \tilde{A}_1$ is convex.

Perhaps mixed volume can be summarized as a mutual measure of size. The properties listed all fit well with this description. For example, the last one says that coordinatewise, mixed volume is a valuation or finitely additive measure. The analogy between mixed volume and determinants points in the same direction: the determinant of $n$ vectors in $\mathbb{R}^n$ is, after all, the volume of the parallelepiped that they generate. But the direct geometric significance of mixed volume remains, to me, elusive.

Posted at August 26, 2011 12:54 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2431

59 Comments & 2 Trackbacks

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I’ll add a puzzle.

I described the analogy between mixed volume and determinant. Now, in linear algebra, the determinant of an operator is often best thought of as the product of its eigenvalues, taken with their algebraic multiplicities. But the spectrum — that is, the set-with-multiplicities of eigenvalues — is really a more fundamental object than the determinant. What is the analogue of the spectrum in the world of convex bodies?

I don’t know the answer.

Posted by: Tom Leinster on August 26, 2011 2:11 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I won’t attempt to say much because I’ll quickly get out of my depth if I do, but the analogies between volumes and determinants are the beginning of a long and — I think — not completely understood story. The creature which is really similar to a mixed volume is called a mixed discriminant. The mixed discriminants of real symmetric matrices $A_1, \ldots, A_n$ are the coefficients in the polynomial expansion of $\det(t_1 A_1 + \cdots + t_n A_n)$ . Mixed discriminants turn out to satisfy many inequalities analogous to those satisfied by mixed volumes. Some brief discussion of this is in section 3.2 of this paper.

I like your puzzle. I have no idea what the answer is, but at a superficial glance it looks like this paper may give some clues.

Posted by: Mark Meckes on August 26, 2011 2:38 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I won’t attempt to say much because I’ll quickly get out of my depth if I do

This made me smile. Mark, if you’re nearly out of your depth, I’m a deep-sea diver.

Mixed discriminants turn out to satisfy many inequalities analogous to those satisfied by mixed volumes.

Beginner that I am, I don’t have much awareness of the inequalities satisfied by mixed volumes. (I keep seeing the phrase “Alexandrov-Fenchel inequalities”, so I’m guessing they’re the main inequalities for mixed volume.)

I was pleased to see this inequality on page 23 of the paper by Giannopoulos and Milman that you cited:

$V(A_1, \ldots, A_n) \geq (Vol(A_1) \cdots Vol(A_n))^{1/n}$

for convex bodies $A_1, \ldots, A_n \subseteq \mathbb{R}^n$ . In other words:

The mixed volume is at least the geometric mean of the individual volumes.

In my post, there were a couple of clues that this might be true:

My first example said that when the sets $A_i$ are all rescalings of each other, equality holds.
The second example involved two rectangles in two-dimensional space: $A = [0, a] \times [0, b], \quad B = [0, c] \times [0, d].$ Their mixed volume $V(A, B)$ is the arithmetic mean of $a d$ and $b c$ . By a famous inequality, $V(A, B)$ is greater than or equal to the geometric mean of $a d$ and $b c$ ; and this is the same as the geometric mean of $a b$ and $c d$ . Hence in this particular case, $V(A, B) \geq \sqrt{Vol(A) Vol(B)}.$

I also mentioned that for arbitary convex bodies $A, B \subseteq \mathbb{R}^2$ ,

$Vol(A + B) = Vol(A) + 2 V(A, B) + Vol(B).$

It follows that

$Vol(A + B) \geq Vol(A) + 2 \sqrt{Vol(A) Vol(B)} + Vol(B)$

or equivalently

$\sqrt{Vol(A + B)} \geq \sqrt{Vol(A)} + \sqrt{Vol(B)}.$

This is the Brunn–Minkowski inequality for convex sets in dimension $2$ . I’m guessing that the same kind of thing works in higher dimensions, i.e. that the Brunn–Minkowski inequality in dimension $n$ can be deduced from the inequality on mixed volumes $V(A_1, \ldots, A_n)$ .

Posted by: Tom Leinster on August 26, 2011 7:10 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I’m confused about which analogy to trust.

I had been thinking of convex bodies in $\mathbb{R}^n$ as analogous to vectors in $\mathbb{R}^n$ , and the mixed volume of an $n$ -tuple of convex bodies in $\mathbb{R}^n$ as analogous to the determinant of an $n$ -tuple of vectors in $\mathbb{R}^n$ . But Mark wrote:

the analogies between volumes and determinants are the beginning of a long and — I think — not completely understood story. The creature which is really similar to a mixed volume is called a mixed discriminant. The mixed discriminants of real symmetric matrices $A_1, \ldots, A_n$ are the coefficients in the polynomial expansion of $\det(t_1 A_1 + \cdots + t_n A_n)$ .

This is a different analogy. It makes convex bodies in $\mathbb{R}^n$ analogous to $n \times n$ matrices, not $n$ -dimensional vectors.

I can try to guess how the analogy mentioned by Mark might work. An $n \times n$ matrix is an $n$ -tuple of $n$ -dimensional vectors, and these generate a parallelepiped in $\mathbb{R}^n$ . So, $n \times n$ matrices can be regarded as special convex bodies in $\mathbb{R}^n$ . You can try to generalize linear algebra constructions and facts to the setting of convex bodies, or specialize in the opposite direction. That seems pretty satisfying.

But $n \times n$ matrices can be multiplied together, so shouldn’t it be possible to multiply together convex bodies in $\mathbb{R}^n$ ? I don’t see how to do this.

On the other hand, I do see the analogue of matrix multiplication if we use the first analogy mentioned in this comment. According to that analogy, vectors in $\mathbb{R}^n$ are like convex bodies in $\mathbb{R}^n$ . An $n \times m$ matrix is an $n$ -tuple of vectors in $\mathbb{R}^m$ , so corresponds to an $n$ -tuple of bodies in $\mathbb{R}^m$ . Let me write

$Hom(m, n)$

for the set of $n$ -tuples of convex bodies in $\mathbb{R}^m$ . The analogue of matrix multiplication would be a canonical map

$\cdot: Hom(m, n) \times Hom(n, p) \to Hom(m, p).$

And there is indeed one of these. I defined it down here, but I’ll say it again: it’s

$((A_1, \ldots, A_n), (B_1, \ldots, B_p)) \mapsto (C_1, \ldots, C_p)$

where

$C_k = \{b_1 \mathbf{a}_1 + \cdots b_n \mathbf{a_n} | (b_1, \ldots, b_n) \in B_k, \mathbf{a}_j \in A_j\}.$

Having an analogue of matrix multiplication makes me prefer this analogy. So, I’m torn. Maybe they’re both good, but good for different things.

Posted by: Tom Leinster on August 26, 2011 8:02 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

In the analogy suggested by what I mentioned, most convex geometers would usually think of a (positive definite) matrix corresponding not to a parallelepiped, but to the ellipsoid which is the unit ball for the inner product given by the matrix. So a matrix here represents a bilinear form, not an operator, which suggests that in this analogy matrix multiplication is not as natural a thing to think about.

Posted by: Mark Meckes on August 26, 2011 8:21 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Following up on this analogy, let $A$ be a positive defnite symmetric matrix, let $E$ be the ellipsoid $v^T A v \leq 1$ and let $B$ be the unit ball. Then, I believe, $\mathrm{Vol}(E+tB) = (\det A)^{-1} \det(t A+\mathrm{Id})$ . This suggests that the analogue of the specturm, for any convex body $K$ , should be the roots of $\mathrm{Vol}(K+tB)$ .

A question I don’t know the answer to: Does this polynomial always have real roots?

Posted by: David Speyer on August 30, 2011 3:18 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

A question I don’t know the answer to: Does this polynomial always have real roots?

$Vol(K + t B)$ , as a function of $t$ , is called the Steiner polynomial of $K$ . So according to this paper which I linked to above, the answer to your question is “no”.

Posted by: Mark Meckes on August 30, 2011 3:29 PM | Permalink | Reply to this

Re: Mixed Volume

Thanks Mark!

Posted by: David Speyer on August 30, 2011 4:07 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Good! That clears things up in a very satisfactory way. Thanks a lot.

Posted by: Tom Leinster on August 26, 2011 8:36 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I keep seeing the phrase “Alexandrov-Fenchel inequalities”, so I’m guessing they’re the main inequalities for mixed volume.

Yes. Essentially all inequalities for mixed volumes are special cases of Alexandrov-Fenchel. This paper by Richard Gardner (an extended version of an article that appeared in the Bulletin of the AMS) is the best place to start learning about this family of inequalities and their interrelationships — check out the figure on page 4.

(Incidentally, there’s a fair amount about entropy and information theory in that paper, too.)

Posted by: Mark Meckes on August 26, 2011 8:06 PM | Permalink | Reply to this

Re: Mixed Volume

Even more so than the determinant, the mixed volume of a set of cuboids looks like the permanent of a matrix.

Posted by: Twan van Laarhoven on August 26, 2011 10:50 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Thanks! I didn’t know that formula had a name. For those who don’t want to click, the permanent of an $n \times n$ matrix $A = (a_{i j})$ is $perm(A) = \sum_{\sigma \in S_n} a_{1, \sigma(1)} \cdots a_{n, \sigma(n)}.$ As the Wikipedia article points out, “[b]oth permanent and determinant are special cases of a more general function of a matrix called the immanant.”

A little while ago I went through the computation that $det(A B) = det(A) det(B)$ directly from the definition of determinant as $\sum_{\sigma \in S_n} sgn(\sigma) a_{1, \sigma(1)} \cdots a_{n, \sigma(n)}.$ (Edit: the following is wrong. See David Speyer’s comment below.) I noticed that the same proof also shows that $perm(A B) = perm(A)perm(B),$ though I didn’t know permanents by name then. Indeed, all that matters about $sgn$ in this proof is that it is a homomorphism from $S_n$ to the multiplicative group $k^\times$ of the ring $k$ over which you’re working. You get permanents by replacing $sgn$ by the trivial homomorphism. Immanants seem to be another family of cases.

I’m disheartened by the Wikipedia article’s statement that

Unlike the determinant, the permanent has no easy geometrical interpretation.

Would you agree with that? Do you have any intuitive understanding (possibly non-geometrical) of what the permanent is?

Posted by: Tom Leinster on August 26, 2011 1:50 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Tom,

you may be amused by this review of a book Permanents by Henryk Minc.

Posted by: Eugene Lerman on August 26, 2011 3:38 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Thanks, Eugene. That’s a review with a sly sense of humour.

The reviewer (Richard A. Brualdi) gives his overall verdict on the importance of permanents:

The book Permanents by Minc is an unlikely book, unlikely because its intent is to give an account of the function, the permanent, as it developed from its inception in 1812 to the present time [1978]. While the permanent function is an interesting, often fascinating, matrix function with applications to [… and here he lists various applications …] it remains, I believe, a matrix function of specialized interest. Certainly it does not rival its relative the determinant for importance in mathematics and its applications.

My impression is that mixed volume has a rather greater importance, at least in the arena of convex geometry.

Posted by: Tom Leinster on August 26, 2011 6:34 PM | Permalink | Reply to this

Re: Mixed Volume

The permanent of a product is not the product of permanents. Try practically any two 2x2 matrices.

Posted by: David Speyer on September 7, 2011 7:28 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Oops. Thanks for setting me straight, David. I see what’s wrong with my “proof” now, but it’s not interesting enough to repeat.

Posted by: Tom Leinster on September 8, 2011 12:02 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

In fact, for any field $k$ , the possible homomorphisms

$GL(k^n) \to k^\times$

are constrained by the fact that the abelianization of $GL(k^n)$ is $k^\times$ , except for some degenerate cases. Indeed, $SL(k^n)$ is equal to its own commutator subgroup unless $n = 2$ and $k$ has only two or three elements (Reference: Lang’s Algebra). Except in those cases, any homomorphism

$GL(k^n) \to k^\times$

must be identically 1 on $SL(k^n)$ , and since $GL(k^n)/SL(k^n) \cong k^\times$ , we conclude

$\hom(GL(k^n), k^\times) \cong \hom(k^\times, k^\times).$

If $k = \mathbb{R}$ , we may conclude that any continuous homomorphism $GL(\mathbb{R}^n) \to \mathbb{R}^\times$ is of the form

$A \mapsto (sign(\det(A)))^n |\det(A)|^\lambda$

for $n = 0$ or $1$ and $\lambda$ some real power.

Posted by: Todd Trimble on September 8, 2011 3:40 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Very neat! David pointed out that I was almost maximally wrong, then Todd provided a razor-sharp analysis of the precise extent to which I was wrong :-)

Seriously, I’m happy to have learned that. Thanks. Todd, I’m so often awed by how much stuff you know.

Posted by: Tom Leinster on September 8, 2011 11:58 PM | Permalink | Reply to this

Re: Mixed Volume

There’s a lot of interesting things about the permanent: computing one is #P-complete, for starters. Scott Aaronson draws an interesting analogy between permanent-determinant on the one hand, and bosons-fermions on the other. This is one of his Powerpoint presentations on the subject, hilarious as usual.

Aaronson is also looking for ways to find the shortest length Straight-Line Program to compute a 4x4 permanent.

Posted by: Jan de Wit on September 13, 2011 2:21 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

The lack of geometrical interpretation - or practially any intuitive interpretation - of the permanent is a well-known thorn in the side of many computational complexity theorists. The #P-completeness of the permanent - together with Toda’s Theorem, and the widely held belief that P is different from NP - lead “common wisdom” in complexity theory to include a conjecture of Les Valiant’s, that computing the permanent is exponentially (or at least more than polynomially) harder than computing the determinant. Proving this is believed to be (at least formally) easier than proving $P \neq NP$ , and yet we are still miles away from proving this seemingly simpler statement.

Any intuitive interpretation of the permanent - specifically, an intuitive interpretation of the permanental hypersurface (the set of matrices whose permanent vanishes) - would go a long way towards this long-sought conjecture. For why the permanental hypersurface enters into the picture, see the current best lower bound on the permanent vs determinant problem and more generally the Geometric Complexity Theory Program.

There are some interpretations in combinatorial settings - e.g. the permanent of a matrix whose entries are all 0 or 1 counts the number of perfect matchings in the associated bipartite graph - but these only seem to take us so far in understanding the permanent in general. For example, using essentially the preceding combinatorial fact, deciding whether the permanent of a nonnegative matrix is zero or nonzero can be done in polynomial time (this paper by Edmonds in which he presents the solution is also one of the primary sources of the entire notion of polynomial-time). But this combinatorial understanding doesn’t seem to help in general: deciding whether the permanent of an arbitrary complex matrix is zero or nonzero is essentially as hard as computing the permanent in the first place (see this cstheory.stackexchange answer, the comments on it, and the references therein), which is at least as hard as all problems in NP by Toda’s Theorem.

Posted by: Joshua Grochow on March 4, 2014 3:49 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Pining for some categories? Well, there’s an algebraic theory whose $n$ -ary operations are the convex bodies in $\mathbb{R}^n$ .

Given convex bodies

$A \in \mathbb{R}^n, B_1 \in \mathbb{R}^m, \ldots, B_n \in \mathbb{R}^m,$

we need to define an $m$ -ary operation, that is, a convex body

$A (B_1, \ldots, B_n) \subseteq \mathbb{R}^m.$

It’s given by

$A (B_1, \ldots, B_n) = \{ a_1 \mathbf{b}_1 + \cdots + a_n \mathbf{b}_n | (a_1, \ldots, a_n) \in A, \mathbf{b}_1 \in B_1, \ldots, \mathbf{b}_n \in B_n\}.$

(It’s easy to check that this is convex.) The identity operation is the convex body $\{1\} \subseteq \mathbb{R}^1$ . The $n$ -ary operation representing $i$ th projection ( $1 \leq i \leq n$ ) is the convex body $\{e_i\} \subseteq \mathbb{R}^n$ , where $e_1, \ldots, e_n$ are the standard basis vectors.

This theory is pretty rich. For example, we can recover Minkowski addition: writing $U_n = \{(1, \ldots, 1)\} \subseteq \mathbb{R}^n$ ,

$A_1 + \cdots + A_n = U_n (A_1, \ldots, A_n)$

for any convex $A_1, \ldots, A_n \subseteq \mathbb{R}^m$ .

Now consider the Lawvere theory of our theory. Its objects are, as always, natural numbers, and a map $m \to n$ is an $n$ -tuple of convex bodies in $\mathbb{R}^m$ . For composition: given

$(A_1, \ldots, A_n) \subseteq \mathbb{R}^m$

(that is, $A: m \to n$ ) and

$(B_1, \ldots, B_p) \subseteq \mathbb{R}^n$

(that is, $B: n \to p$ ), the resulting tuple

$(C_1, \ldots, C_p) \subseteq \mathbb{R}^m$

(namely, $B \circ A: m \to p$ ) is given by

$C_k = B_k (A_1, \ldots, A_n)$

( $1 \leq k \leq p$ ).

This is rather like the category of finite-dimensional vector spaces, or better, its skeleton $Mat$ whose objects are natural numbers and whose maps are matrices. Since every vector space is free, $Mat$ is the opposite of the Lawvere theory of vector spaces. And by duality for finite-dimensional vector spaces, it doesn’t matter whether we say the words “the opposite of”.

In the post, I was drawing an analogy between $n$ -tuples of convex bodies in $\mathbb{R}^n$ and $n$ -tuples of vectors in $\mathbb{R}^n$ — that is, $n \times n$ matrices, or linear endomorphisms of $\mathbb{R}^n$ . If that analogy is good, we should be able to compose any two $n$ -tuples of convex bodies in $\mathbb{R}^n$ . And the stuff above shows that you can! It’s composition in the Lawvere theory.

And there’s no need to stick to endomorphisms: for any $m$ , $n$ and $p$ , you can compose an $p$ -tuple of bodies in $\mathbb{R}^n$ with an $n$ -tuple of bodies in $\mathbb{R}^m$ , to get a $p$ -tuple of bodies in $\mathbb{R}^m$ . It’s just like matrix multiplication.

Posted by: Tom Leinster on August 26, 2011 2:35 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Just because it took me some while to grok this, I’ll toss in that an $n$ -tuple of convex bodies in $\mathbb{R}^m$ is “the same as” a convex family of linear maps $\mathbb{R}^n\to \mathbb{R}^m$ . Composition as described above is in the same way “the same as” taking families of composites.

I also think there should be something to say about how a convex body in $\mathbb{R}^n$ containing the origin nearly defines a metric on $\mathbb{R}^n$ … but I’ll have to let it stew some more.

Posted by: some guy on the street on August 26, 2011 8:45 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Some guy, thanks for your comment, but I’m a bit puzzled by this:

an $n$ -tuple of convex bodies in $\mathbb{R}^m$ is “the same as” a convex family of linear maps $\mathbb{R}^n \to \mathbb{R}^m$ .

I assume you’re referring to the fact that the set $Hom(\mathbb{R}^n, \mathbb{R}^m)$ of linear maps $\mathbb{R}^n \to \mathbb{R}^m$ has a vector space structure. So, given a subset $F \subseteq Hom(\mathbb{R}^n, \mathbb{R}^m)$ , it makes sense to ask whether $F$ is convex. And if I understand correctly, you’re saying that an $n$ -tuple of convex bodies in $\mathbb{R}^m$ is the same thing as a (compact, nonempty) convex subset of $Hom(\mathbb{R}^n, \mathbb{R}^m)$ .

But this doesn’t seem to be true. Take $n = 2$ and $m = 1$ . Then an $n$ -tuple of convex bodies in $\mathbb{R}^m$ is a pair of (compact, nonempty) intervals in the real line. On the other hand, a convex subset of the vector space

$Hom(\mathbb{R}^n, \mathbb{R}^m) = Hom(\mathbb{R}^2, \mathbb{R}) \cong \mathbb{R}^2$

is a convex subset of the plane. Is a pair of intervals in the line the same thing as a convex subset of the plane? That seems unlikely.

Certainly every pair $A_1, A_2$ of intervals in $\mathbb{R}$ gives rise to a convex subset of $\mathbb{R}^2 \cong Hom(\mathbb{R}^2, \mathbb{R})$ , namely $A_1 \times A_2$ . But not every convex subset of $\mathbb{R}^2$ arises in this way.

Posted by: Tom Leinster on August 27, 2011 7:05 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

oh? oh dear… it’s terribly annoying when the nice-seeming idea doesn’t work! As it happens, what I thought I’d “grok”ed was how the composition defined before ends up being a convex thing… but it seems I was more confused than previously expected!

And I’m sorry in case of proliferating confusion rather than good ideas.

Posted by: some guy on the street on August 29, 2011 9:01 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

It is a nice-seeming idea! And I’m not sure that all is lost.

We still have a way of turning an $n$ -tuple of convex bodies in $\mathbb{R}^m$ into a subset of $Hom(\mathbb{R}^n, \mathbb{R}^m)$ , as you originally said. Write $e_1, \ldots, e_n$ for the standard basis of $\mathbb{R}^n$ . Then, given convex bodies $A_1, \ldots, A_n \subseteq \mathbb{R}^m$ , we get a subset $F \subseteq Hom(\mathbb{R}^n, \mathbb{R}^m)$ defined by

$F = \{ f \in Hom(\mathbb{R}^n, \mathbb{R}^m) | f(e_i) \in A_i for each i \}.$

If you view $Hom(\mathbb{R}^n, \mathbb{R}^m)$ as $(\mathbb{R}^m)^n$ , then $F$ becomes simply $A_1 \times \cdots \times A_n$ . So $F$ is convex.

OK, now take an $n$ -tuple $(A_1, \ldots, A_n)$ of convex bodies in $\mathbb{R}^m$ , with its corresponding convex body $F \subseteq Hom(\mathbb{R}^n, \mathbb{R}^m)$ . Also take a $p$ -tuple $(B_1, \ldots, B_p)$ of convex bodies in $\mathbb{R}^n$ , with its corresponding convex body $G \subseteq Hom(\mathbb{R}^p, \mathbb{R}^n)$ . Finally, let $H \subseteq Hom(\mathbb{R}^p, \mathbb{R}^m)$ be the convex body corresponding to the “composite”

$(C_1, \ldots, C_p) = (A_1, \ldots, A_n)(B_1, \ldots, B_p).$

Question: what is $H$ in terms of $F$ and $G$ ?

As I understood it, you were suggesting that

$H = \{ f \circ g | f \in F, g \in G \}.$

That would be excellent, and would maybe be the best point of view on composition of tuples of convex bodies. But I haven’t yet sat down and convinced myself that this is true.

Posted by: Tom Leinster on August 29, 2011 9:15 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I’m at a conference on convex and integral geometry in Frankfurt. It began with a very nice talk from Richard Gardner, in which among other things he mentioned this algebraic theory in which the $n$ -ary operations are the convex bodies in $\mathbb{R}^n$ .

Well, actually, he didn’t refer to it as an algebraic theory. He used the term “ $A$ -combination” for the operation that sends an $n$ -tuple of convex bodies $B_1, \ldots, B_n \subseteq \mathbb{R}^m$ to

$A(B_1, \ldots, B_n) = \{ \sum_i a_i \mathbf{b}^i : (a_1, \ldots, a_n) \in A, \mathbf{b}^i \in B_i \}.$

Here $A$ is a convex body in $\mathbb{R}^n$ . Gardner said that he looked in the literature to find the origins of this construction, and traced it to a 1997 paper of Protasov.

I started wondering if this theory had any interesting algebras. It turns out that it does, at least if you restrict to convex subsets of $[0, \infty)^n$ . Convex geometers make extensive use of the support function $h_A$ of a convex body $A \subseteq \mathbb{R}^n$ , which is the function $h_A: \mathbb{R}^n \to \mathbb{R}$ given by

$h_A(u) = \sup \{ \langle a, u \rangle : a \in A \}.$

(Usually they restrict $h_A$ to $S^{n - 1}$ . You can reconstruct $A$ from $h_A$ , or this restriction.)

And this construction makes $\mathbb{R}$ into an algebra for our weird theory! I don’t know what to make of this yet, but as support functions are so important, I’m pleased that this works out.

Posted by: Tom Leinster on September 28, 2011 7:44 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Tom, I haven’t had a chance to look closely at your post, but what I glanced at, such as the picture you have near Steiner’s theorem, reminds me of Milnor’s proof of the ‘hairy ball theorem’, that there are no non-vanishing vector fields on an even-dimensional sphere. (Ha, possible tie-in there with Mike’s recent post on indexes of vector fields! (-: ). I’m wondering whether you’ve seen this proof.

I first heard this proof from John Baez when he and I were together in England about a dozen years ago. It is quite a surprising proof, which I can follow line by line as it were, but don’t understand at a deep level. But I surmise it must have something to do with things like relationships between Weyl’s tube formulas and characteristic classes. Since you’ve been thinking about related matters, I thought you might have some insight here.

Posted by: Todd Trimble on August 27, 2011 8:26 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Todd, thanks, as always, for the learned comments. I must have seen that post before, because I remember the bit at the beginning where you recount how John made you fall off your bar stool. But I didn’t actually read the hard bit :-)

At the moment, I have nothing to contribute. At the intuitive level, there’s an obvious connection between $\varepsilon$ -neighbourhoods as used in Steiner’s theorem and tubular neighbourhoods as used in differential geometry. I believe this connection is well exploited in integral geometry. Anyway, I should read your account of Milnor’s proof!

Posted by: Tom Leinster on August 27, 2011 9:49 PM | Permalink | Reply to this

Is there some version of Hadwiger’s theorem?

I’d like to check my understanding: the intrinsic volumes are a special case of the mixed volumes (scaled by some factor) involving a convex body of interest and a unit ball. In general, mixed volumes take as input multiple convex bodies, whereas intrinsic volumes take only one.

Hadwiger’s theorem states that the intrinsic volumes form a basis for “measures of size” (continuous isometry-invariant valuations on convex sets).

Is there a generalization of Hadwiger’s theorem to something like “mutual” measures of size that maybe singles out the mixed volumes as a basis? (Does this question make sense, even?)

Posted by: jc on August 28, 2011 9:39 PM | Permalink | Reply to this

Re: Is there some version of Hadwiger’s theorem?

$MathML-enabled post (click for more details).$

Hi jc.

the intrinsic volumes are a special case of the mixed volumes (scaled by some factor) involving a convex body of interest and a unit ball.

Yes indeed.

For the benefit of those who don’t already know, here’s how this works. I gave the general formula for the volume of a linear combination of convex bodies $A_1, \ldots, A_k \subseteq \mathbb{R}^n$ :

$Vol(t_1 A_1 + \cdots t_k A_k) = \sum_{n_1 + \cdots + n_k = n} \frac{n!}{n_1 ! \cdots n_k !} V(A_1^{n_1}, \ldots, A_k^{n_k}) t_1^{n_1} \cdots t_k^{n_k}$

where $A^i$ means $i$ copies of $A$ . Taking $k = 2$ and $t_1 = t$ , and changing some letters, this says

$Vol(A + t B) = \sum_{i = 0}^n \binom{n}{i} V(A^i, B^{n - i}) t^{n - i}.$

In particular, this is true when $B$ is the $n$ -dimensional unit ball $B_n$ . On the other hand, Steiner’s theorem is that

$Vol(A + t B_n) = \sum_{i = 0}^n V_i(A) \omega_{n - i} t^{n - i}$

where $\omega_j$ is the volume of the $j$ -dimensional unit ball (for which there is a well-known formula). Comparing coefficients, we deduce that for an arbitrary convex body $A \subseteq \mathbb{R}^n$ ,

$V_i(A) = c_i V(A, \ldots, A, B_n, \ldots, B_n)$

with $i$ copies of $A$ and $n - i$ copies of the unit ball $B_n$ . Here $c_i$ is the positive constant $\binom{n}{i}/\omega_{n - i}$ .

Is there a generalization of Hadwiger’s theorem to something like “mutual” measures of size that maybe singles out the mixed volumes as a basis? (Does this question make sense, even?)

I don’t know! I think this is an excellent question. It seems that this or similar questions have been the basis of recent research: see for instance

Vitali Milman, Rolf Schneider, Characterizing the mixed volume.

The three-axiom characterization at the beginning of my post has the weakness that it already assumes we know what volume is. Milman and Schneider are looking for a characterization without this weakness. They only get partial answers, so it seems that the question is open.

Posted by: Tom Leinster on August 28, 2011 10:07 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Can you say anything about why an invariant with a name related to “volume” should be restricted to nonempty, convex regions? Ordinarily, empty and nonconvex regions have volume just as well as nonempty convex ones.

Posted by: Mike Shulman on August 29, 2011 11:50 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Thanks for asking that, Mike. (I sound like a politician: “I’m glad you asked me that”…) I’ve been imagining that some of the regulars here are thinking to themselves “why’s he going on about convex sets so much these days?”

I think to a large extent it’s about the art of the possible. Quantities like volume and perimeter are certainly defined for a much larger class of spaces than convex subsets of $\mathbb{R}^n$ . No one pretends otherwise, and there’s been a lot of effort expended on extending what’s known about convex sets to different kinds of space. However, convex sets do provide an arena in which things tend to work in a controllable way. You might even call them a “toy model” if your aim was to handle more general spaces.

Let me give two examples of how convex sets are particularly amenable.

First, volume is continuous. What I mean by this is that Lebesgue measure

$Vol: \{compact subsets of \mathbb{R}^n\} \to \mathbb{R}$

is discontinuous (with respect to the Hausdorff metric), but continuous when restricted to convex sets. For example, if $k$ is large then the subset $\{0, 1/k, 2/k, \ldots, k/k = 1\}$ of $\mathbb{R}^1$ is close in the Hausdorff metric to $[0, 1]$ , but their Lebesgue measures are very different.

Second, if you want to add together subsets of $\mathbb{R}^n$ (take their Minkowski sums) then convexity is a convenient assumption. Consider, for example, the distributivity laws

$X + (Y \cup Z) = (X + Y) \cup (X + Z), \quad X + (Y \cap Z) = (X + Y) \cap (X + Z)$

for closed sets $X, Y, Z \subseteq \mathbb{R}^n$ . The first one is always true, trivially. The second one is in general false — but it’s true if $Y \cup Z$ (sic!) is convex.

As you know, I’m trying to understand a whole lot of things to do with size. Some of the questions that have arisen are pretty difficult. For example, there are conjectures about magnitude of metric spaces that are natural from a conceptual point of view, yet present analytical obstacles that we’ve been unable to overcome. Even the convex world, which is supposed to be easy, is hard, but there’s some evidence that it’ll be less hard. For example, we do at least think we know an explicit formula for the magnitude of a convex set, even though we can’t prove it.

So that’s why I’ve been going on about convex sets. I think I’ll leave the nonemptiness to another comment — that’s really a different issue.

(PS: I notice you called them convex “regions” rather than sets. I know, “set” is kind of a crappy word in this context, but I’m afraid I’ve picked up the habit now…)

Posted by: Tom Leinster on August 30, 2011 12:18 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

The question of nonemptiness is really interesting, I think. It might seem thoroughly unpromising, but it’s changed my understanding of the meaning of convexity.

Lots of authors in convex geometry include the condition of nonemptiness (as well as compactness) in the term “convex set” or “convex body”. I used to react to that as many category theorists probably would: I assumed it was just part of that ancient bad habit you see throughout mathematics texts. But reading about mixed volume made me question that belief.

Suppose we allow $\emptyset$ as a convex body. Then however we define mixed volume on possibly-empty convex bodies, the multiadditivity property (number 3) fails. First note that $\emptyset$ is… absorbent? absorptive?… with respect to Minkowski sum:

$\emptyset + A = \emptyset$

for all $A$ . Taking $\tilde{A}_1 = \emptyset$ in the multiadditivity axiom therefore gives

$V(\emptyset, A_2, \ldots, A_n) = V(A_1, A_2, \ldots, A_n) + V(\emptyset, A_2, \ldots, A_n)$

and so $V \equiv 0$ , which is false. So if we want to keep the multiadditivity property — which is rather appealing — then we’d better forbid the empty set from being a convex body.

At first that seems entirely unsatisfactory, just as it would be unsatisfactory to exclude $\emptyset$ from being a topological space or $\{0\}$ from being a ring. But recently I’ve been thinking that perhaps convex bodies should be thought of as like prime numbers, or connected spaces: they’re the building blocks. In the same way that $1$ should not be counted as prime and $\emptyset$ should not be counted as connected, $\emptyset$ should not be counted as convex. Some evidence for this is that “polyconvex” sets — finite unions of convex sets — are known to be a useful class of spaces.

At the moment I’m not sure what I think; I’m just trying out this viewpoint (“convexity is like primality”) for size.

Posted by: Tom Leinster on August 30, 2011 12:44 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Good and thought-provoking answers.

Lebesgue measure is discontinuous (with respect to the Hausdorff metric)

Hmm, true. I don’t suppose that might mean that the Hausdorff metric is the wrong topology to put on non-convex regions?

Second, if you want to add together subsets of $ℝ^n$ (take their Minkowski sums)

Can you say anything about why you might want to do that? I’m sure there are good reasons, but the Minkowski sum looks kind of unmotivated to me when thinking about “volume.”

recently I’ve been thinking that perhaps convex bodies should be thought of as like prime numbers, or connected spaces: they’re the building blocks

That’s certainly an intriguing viewpoint. Can you extend the definition of mixed volume to polyconvex sets in a consistent way (i.e. not depending on the decomposition into convex sets)? I guess multiadditivity wouldn’t hold any more, but some of the other properties might.

Posted by: Mike Shulman on August 30, 2011 4:52 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

As a part-time convex geometer, it’s never occured to me (except maybe when reading the first couple pages of a book, going through the fundamental definitions) that one might want $\emptyset$ to count as convex. On some brief reflection, my take is that it would be rather like counting $\emptyset$ as a vector space. In particular, there’s a nice monoid structure on convex sets given by Minkowski addition, and $\{ 0 \}$ , not $\emptyset$ , is the identity.

Lebesgue measure is discontinuous (with respect to the Hausdorff metric)

Hmm, true. I don’t suppose that might mean that the Hausdorff metric is the wrong topology to put on non-convex regions?

Of course the response to such a question has to be “Wrong for what purpose?” But yes, I’d agree that for many purposes it probably is wrong. The space of convex bodies has in many ways quite different behavior from the space of all sets in $\mathbb{R}^n$ .

Second, if you want to add together subsets of ℝ n (take their Minkowski sums)

Can you say anything about why you might want to do that? I’m sure there are good reasons, but the Minkowski sum looks kind of unmotivated to me when thinking about “volume.”

I can say something about that. A long answer consists of this book; the “Brunn–Minkowski theory” of its title refers to the entire body of results relating volume and Minkowski sums. For a shorter answer, consider the Brunn–Minkowski theorem: $Vol(A + B)^{1/n} \ge Vol(A)^{1/n} + Vol(B)^{1/n}$ for nonempty compact sets $A, B \subseteq \mathbb{R}^n$ . (Note this is false if $A$ or $B$ is empty! Also, unlike some of the other results mentioned above, this theorem doesn’t require convexity.) This is an extremely important result with many applications. Here are two of the most famous.

The surface area of a regular enough set $A \subseteq \mathbb{R}^n$ can be defined as $S(A) = \lim_{\varepsilon \to 0^+} \frac{Vol(\{x : d(x,A) \le \varepsilon\}) - Vol(A)}{\varepsilon}.$ But lurking in that formula is a Minkowski sum: $\{ x : d(x,A) \le \varepsilon\} = A + \varepsilon B$ , where $B$ is the Euclidean unit ball. The Brunn–Minkowski inequality says that $Vol(A + \varepsilon B) \ge (Vol(A)^{1/n} + \varepsilon Vol(B)^{1/n})^n \ge Vol(A) + n \varepsilon Vol(B)^{1/n} Vol(A)^{(n-1)/n} + o(\varepsilon),$ from which it follows that $S(A) \ge \left(\frac{Vol(A)}{Vol(B)}\right)^{(n-1)/n} S(B).$ In other words, we’ve recovered the isoperimetric inequality in $\mathbb{R}^n$ .

For the second application, let $K \subset \R^n$ be a convex body (by which I mean a compact, convex set with nonempty interior), and fix $\theta \in S^{n-1}$ . For $t \in \R$ let $K_t = K \cap \{ x : \langle x, \theta \rangle = t \}.$ By the convexity of $K$ , $K_t \supset \lambda K_s + (1 - \lambda) K_u$ whenever $t = \lambda s + (1 - \lambda) u$ and $0 \le \lambda \le 1$ . Then the Brunn–Minkowski theorem implies that $Vol(K_t)^{1/(n-1)}$ is a concave function on its support (here $Vol$ stands for $(n-1)$ -dimensional Lebesgue measure). In particular, it is unimodal (increases, then decreases). In particular, if $K$ is symmetric about $\{ 0 \}$ , then in every direction the cross-section of greatest $(n-1)$ -dimensional volume is the one through the origin. This fact seems geometrically obvious, but I don’t know of any simpler proof.

Posted by: Mark Meckes on August 30, 2011 3:23 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Mark wrote:

As a part-time convex geometer, it’s never occured to me (except maybe when reading the first couple pages of a book, going through the fundamental definitions) that one might want $\emptyset$ to count as convex.

This and a couple of other things make me think that I’ve been slightly warped by Klain and Rota’s book, which was the first thing on convex-ish geometry that I read in depth. It seems that it’s eccentric in a few respects, including this. They definitely do take $\emptyset$ to be convex. Apart from the fact that when they define “convex”, they don’t add the condition of nonemptiness, they also put “ $\phi(\emptyset) = 0$ ” into the definition of convex valuation.

I suppose also that nonemptiness seemed artificial to me because it appeared to be tacked on to the definition of convexity for no apparent reason. I don’t really see it as similar to the case of vector spaces. There, you don’t need to say “nonempty” explicitly: nonemptiness follows from the presence of the zero element, which is a well-motivated part of the structure.

But it seems that $\emptyset$ really shouldn’t be called convex.

I note that this does make one thing more complicated (which is not to say “bad”). The class $\mathcal{K}^n$ of convex compact subsets of $\mathbb{R}^n$ is no longer closed under intersections, even binary intersections. However, we do have

$A, B, A \cup B \in \mathcal{K}^n \implies A \cap B \in \mathcal{K}^n.$

Maybe this is all that matters if we’re primarily interested in valuations. In fact, this is exactly the situation for $\ell_1$ -convex subsets of $\mathbb{R}^n$ : it’s not closed under intersections, but if the union of two compact $\ell_1$ -convex sets is $\ell_1$ -convex then so is their intersection.

the Brunn–Minkowski theorem implies that $Vol(K_t)^{1/(n - 1)}$ is a concave function on its support

Could you supply a small hint about this step?

Posted by: Tom Leinster on August 30, 2011 5:27 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

This and a couple of other things make me think that I’ve been slightly warped by Klain and Rota’s book, which was the first thing on convex-ish geometry that I read in depth.

That’s another exception I should add, then: I did read their book, and for their purposes it definitely did seem natural to take $\emptyset$ to be convex. (They notably make very little mention of Minkowski addition.) That book isn’t about the kinds of convex geometry I usually think about. Now that I think about it more carefully, I imagine it may also be convenient to consider $\emptyset$ to be convex in combinatorial convexity.

It seems that it’s eccentric in a few respects, including this.

It certainly is. I take issue with some of their eccentricities, but in their context I don’t really take issue with this one.

I don’t really see it as similar to the case of vector spaces. There, you don’t need to say “nonempty” explicitly: nonemptiness follows from the presence of the zero element, which is a well-motivated part of the structure.

Yes, that’s a definite weakness in my analogy. Suppose instead I mentioned subspaces of $\mathbb{R}^n$ , defined not as subsets which are vector spaces with the operations inherited from $\mathbb{R}^n$ , but as subsets closed under addition and scalar multiplication. By that definition $\emptyset$ is a subspace of $\mathbb{R}^n$ unless you explicitly exclude it, and it would be easy to come up with reasons to exclude it other than the fact that it’s not a vector space.

In any case, I stand by my claim that the presence of $\emptyset$ would be unpleasant for the algebraic structure of $\mathcal{K}^n$ (which may or may not be relevant, depending on what you care about).

the Brunn–Minkowski theorem implies that $Vol(K_t)^{1/(n−1)}$ is a concave function on its support

Could you supply a small hint about this step?

The $(n-1)$ -dimensional convex bodies $K_s$ and $K_u$ lie in parallel hyperplanes; think of translating them to lie in the same hyperplane as $K_t$ . After estimating $Vol(K_t)$ from below by the inclusion I noted, apply Brunn–Minkowski to $\lambda K_s$ and $(1-\lambda)K_u$ in that hyperplane, and use the homogeneity of volume.

Posted by: Mark Meckes on August 30, 2011 6:23 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Apropos of Dan Klain and Gian-Carlo Rota’s book Introduction to Geometric Probability (which has a nice Bull. AMS review), Mark wrote:

I take issue with some of their eccentricities

If you feel like expanding on that, I’d be interested to hear it!

Back to why (and whether) the empty set shouldn’t be counted as convex: it did occur to me that some onlookers might be amused at me writing paragraph after paragraph about the empty set. I thought of several justifications, then I realized that I didn’t really care if people were amused. It’s nice to bring amusement to people’s lives, and anyway I think this kind of thing matters.

Suppose instead I mentioned subspaces of $\mathbb{R}^n$ , defined not as subsets which are vector spaces with the operations inherited from $\mathbb{R}^n$ , but as subsets closed under addition and scalar multiplication. By that definition $\emptyset$ is a subspace of $\mathbb{R}^n$ unless you explicitly exclude it, and it would be easy to come up with reasons to exclude it other than the fact that it’s not a vector space.

I have a slightly different take on this. When people talk about a subset of some algebraic structure being closed under addition, or multiplication, or some other associative unital operation, they often only say it for the binary case, especially in casual conversation. But often they really want it to hold for the nullary case, too. Closure under binary addition implies closure under $n$ -fold addition for all $n \geq 1$ :

$x_1, \ldots, x_n \in A \implies x_1 + \cdots + x_n \in A.$

But it doesn’t imply the case $n = 0$ , where this statement reads simply “ $0 \in A$ ”. And often it’s unhelpful to make a special case of $n = 0$ .

So if someone told me they wanted to consider subsets of $\mathbb{R}^n$ closed under addition, I’d probably assume that they wanted closure under nullary as well as binary addition. Then the empty set doesn’t qualify. Of course, they might not want closure under nullary addition, i.e. they might want $\emptyset$ to be a subspace, for some particular reason.

Here are two possible definitions of convex set. Let $A \subseteq \mathbb{R}^n$ .

$A$ is convex if for all $n \geq 0$ , for all $(\lambda_1, \ldots, \lambda_n) \in [0, \infty)^n$ , $\sum_i (\lambda_i A) = (\sum_i \lambda_i) A$
Same, but only quantifying over $(\lambda_1, \ldots, \lambda_n) \in [0, \infty)^n$ such that $\sum_i \lambda_i = 1$ .

These do not give quite the same result. In both definitions, the inclusion $\supseteq$ of the equation is trivial; it’s $\subseteq$ that’s in question. In both definitions, the case $n = 1$ is trivially true, and the case $n = 2$ implies all the cases $n \geq 2$ . Moreover, the case $n = 2$ of the first definition is equivalent to the case $n = 2$ of the second: they both say that $A$ is convex or empty. So the only possible difference is the case $n = 0$ . There, the first definition says $\{0\} = 0 A$ , i.e. $A \neq \emptyset$ . But the second definition is vacuously true, since there are no $0$ -tuples $\lambda$ satisfying $\sum_i \lambda_i = 1$ .

So the first definition excludes $\emptyset$ as a convex set, and the second definition includes it.

[Mark’s hint about applying the Brunn-Minkowski inequality]

Thanks! Got it.

Posted by: Tom Leinster on August 30, 2011 9:43 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

anyway I think this kind of thing matters.

Me too!

I don’t really see it as similar to the case of vector spaces. There, you don’t need to say “nonempty” explicitly: nonemptiness follows from the presence of the zero element, which is a well-motivated part of the structure.

Me too.

So if someone told me they wanted to consider subsets of $\mathbb{R}^n$ closed under addition, I’d probably assume that they wanted closure under nullary as well as binary addition.

Me too.

Here are two possible definitions of convex set.

This is very intriguing. It occurs to me that there is an analogous situation with affine spaces and more generally heaps. Both affine spaces and convex spaces can be defined abstractly as algebras for some algebraic theory—except for a requirement of nonemptiness. In the case of affine spaces, one needs nonemptiness for the correspondence with vector spaces to work, since a vector space is of course nonempty.

Posted by: Mike Shulman on August 31, 2011 4:54 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I have a slightly different take on this. When people talk about a subset of some algebraic structure being closed under addition, or multiplication, or some other associative unital operation, they often only say it for the binary case, especially in casual conversation. But often they really want it to hold for the nullary case, too

That’s a good point. In any case, the more I think about it the more I see that for some purposes it makes sense to count $\emptyset$ as convex. But in many subfields (including those I’m most familiar with) it appears to be a rather pathological convex set which would need to be explicitly excluded to make important results true, so if nothing else it’s more economical to exclude it from the definition in the first place.

It’s nice to bring amusement to people’s lives,

This is a wonderful philosophy!

and anyway I think this kind of thing matters.

It definitely matters to have the right definitions. I’m coming to the conclusion that the right definition of convex set unfortunately depends on the context.

I take issue with some of their [Klain and Rota’s] eccentricities

If you feel like expanding on that, I’d be interested to hear it!

Well, I should certainly start by emphasizing that it’s a beautiful, and beautifully written, book. My “issues” are both minor and curmudgeonly.

My first issue is with the title Geometric Probability, which the authors say is “sometimes already renamed integral geometry”. As most people use these terms, integral geometry is a separate field which grew out of geometric probability but has a life of its own. In fact Klain and Rota’s book is really about integral geometry, including a bit of geometric probability for motivation and illustration.

I was also put off by this rather smug passage in the preface:

First, we investigate measures on polyconvex sets … that are invariant under the group of Euclidean motions. A great many mathematicians are still basking in the illusion that there is only one such measure, namely, the volume. We merrily destroy this illusion…

Of course there is only one such measure (up to normalization, and say $\sigma$ -finiteness) if by “measure” you mean what most mathematicians usually mean by that word. You need to read quite a bit further to realize that here (but not everywhere in the book) the authors write “measure” but mean “valuation”. There are some other instances of unacknowledged nonstandard use of terminology.

My biggest issue is with the cavalier use of phrases like “random translation” and other references to “random” objects drawn from a space with a canonical infinite measure. In the book, of course, one can make perfect sense of each such object. What the authors do, though, is simply assert that the expectation of such-and-such a quantity depending on the “random translation” is given by such-and-such an integral (over a finite measure space), without ever explaining how to honestly see the random object as a function defined on a probability space. I recognize that the book’s purpose is to develop the geometric ideas with a minimum of fuss, but this kind of issue seriously bedeviled attempts to understand probability prior to Kolmogorov. The authors suggest that the book is accessible to advanced undergraduates, whose intuition about probability I fear could be badly damaged (or at least, fail to be enlightened) by the failure at least to admit that there’s a subtle and important issue in making sense of such things.

(For the curious, the resolution of the specific example I had in mind is that although a random translation of $\mathbb{R}^n$ is nonsense, what’s actually being considered is a random translation of a lattice in $\mathbb{R}^n$ . The (infinite) translation-invariant measure on the translation group induces a finite translation-invariant measure on the space of cosets of the lattice.)

To end, I will admit that while preparing to write about another of my complaints, about a key result including a term that the authors failed to define, I discovered that they had defined it, in a paragraph on the previous page that I apparently consistently overlooked.

Posted by: Mark Meckes on August 31, 2011 4:38 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I’m coming to the conclusion that the right definition of convex set unfortunately depends on the context.

Hmm, maybe not, actually. For the structures and results I’m interested in that fail for $\emptyset$ , there are other natural conditions that exclude $\emptyset$ anyway. In particular, I’m usually interested in compact convex sets of a given (positive) dimension (meaning the dimension of the affine hull).

Posted by: Mark Meckes on August 31, 2011 5:20 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

What about Brunn–Minkowski? I know that holds for arbitrary nonempty compact sets, but in particular it holds for nonempty convex sets.

Posted by: Tom Leinster on August 31, 2011 5:34 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Well, Brunn–Minkowski is just true in an unreasonable level of generality. But for its applications to convexity one (like the one I described about hyperplane sections here or the one I described here) one is typically thinking of a convex body equipped with normalized volume as a probability space. Even for $0$ -dimensional “bodies” one can make sense of this, but not for $\emptyset$ .

Posted by: Mark Meckes on August 31, 2011 7:23 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

One more complaint, and then I promise I’ll stop (and I reiterate that I really do think it’s a very nice book!). The authors are actually rather fuzzy about the domain on which valuations, including the Euler characteristic, are defined. They state that they consider them on what they call $Polycon(n)$ , which they define as the set of all compact convex subsets of $\mathbb{R}^n$ ; they make rather a big deal of this as the right domain. But they then compute the Euler characteristic of the relative interior of a convex polytope, which is never compact; this calculation is subsequently applied to prove other results. Again, this can be fixed, but I found the cognitive dissonance quite distracting.

Posted by: Mark Meckes on September 1, 2011 2:46 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

One thing that’s bothered me is whether Klain and Rota show that volume is continuous as a function $\{convex subsets of \mathbb{R}^n\} \to \mathbb{R},$ with respect to the Hausdorff metric on the domain. They surely need to prove that, either directly or indirectly, because they need to know that volume is a continuous valuation. I remember looking for a proof and not finding it there. But then, I didn’t look enormously hard (because I’ve seen proofs elsewhere), so maybe they do cover it. I don’t have my copy here now to check.

I’ve wondered sometimes whether I could use the book for an advanced undergraduate project. I think, though, that it would be too difficult for someone who didn’t know a bit about measures, and our undergrads probably don’t.

Posted by: Tom Leinster on September 2, 2011 12:11 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I’ve just had a look and I can’t find it. On p. 44 is the assertion, without proof or reference, that volume is continuous. Chapter 8 is all about characterizations of volume, in the sense that under certain circumstances a valuation must be a scalar multiple of volume. But as far as I can see they never prove that there exist nonzero examples of such valuations.

Posted by: Mark Meckes on September 2, 2011 3:58 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

That’s all very interesting, Mark. Anyone who reads the preface to Klain and Rota’s book must surely be struck by the passage you quoted:

First, we investigate measures on polyconvex sets … that are invariant under the group of Euclidean motions. A great many mathematicians are still basking in the illusion that there is only one such measure, namely, the volume. We merrily destroy this illusion…

The more I ponder it, the more fuzzy the thinking behind this seems to be — though of course the writing is very sharp. Interpreting “measure” in the standard way, what they’re implying is simply false, as you point out. OK: so “measure” has to be interpreted in some looser way. But every mathematician is well aware that there are other ways to “measure” subsets of $\mathbb{R}^n$ , or at least reasonably regular ones: everyone knows about perimeter and surface area, for instance.

I wonder whether they were just trying to be provocative. Maybe they assumed the reader would think “wait, that’s false” and think next “so there must be non-obvious sense in which it’s true” and thereby be stimulated into finding out what that sense is. But the danger of being provocative is that the reaction you provoke might not be the one you want.

To me the big surprise — and the big secret revealed by this part of integral geometry — is that along with well-known “measures” such as volume and surface area, there are a whole lot of other ones that most mathematicians are unaware of (namely, the intrinsic volumes). And a closely related surprise is that Euler characteristic is a member of this family, which gives a quite different point of view on what Euler characteristic is. But they do say that in their preface.

I should also add that I like the book very much and I’ve learned a lot from it. Though actually, I didn’t really get into it for a year or two after I bought it. What stopped me was, in fact, their treatment of randomness, quite near the beginning. I thought I was simply failing to understand it, so I’m relieved to hear that actually they just weren’t being rigorous.

I’m not sure I’ve really stopped to think about this before, but it’s really not obvious how you make Buffon’s needle problem precise, is it? I mean the question, not the answer.

Eventually I stopped trying to read Klain and Rota linearly, and started picking it up whenever I felt like it, reading whichever part I wanted to. And after a while, I realized I’d covered most of the book.

There’s another memorable passage in the preface:

Second, we prove the fundamental formula of integral geometry, viz., the kinematic formula. Here we displace the common device of Minkowski sums from its typically central role, not merely as a display of mathematical machismo, but with an ulterior motive.

I love the insertion of the word “merely”. I suppose it’s kind of obnoxious, but mostly I find it funny.

Posted by: Tom Leinster on September 2, 2011 12:03 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

…a closely related surprise is that Euler characteristic is a member of this family, which gives a quite different point of view on what Euler characteristic is.

Does this suggest ways to extend the range of things the rest of the family can measure, along the lines of your extension of the Euler characteristic to categories? The intrinsic volumes of a category?

Posted by: David Corfield on September 2, 2011 9:39 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Ah, now that’s a very Corfieldy comment. Thanks for the idea! But (and this isn’t so typical for your comments) I don’t think it’s going to work. At least, I don’t see a way of making it work.

There are at least two really special features of subsets of $\mathbb{R}^n$ (viewed as metric spaces) among arbitrary enriched categories. Those features are somehow important to the existence of the intrinsic volumes.

First is that the enriching category for metric spaces is exceptionally rich in automorphisms. By the “enriching category” I mean $V = ([0, \infty], \geq, +, 0)$ . Its group of monoidal automorphisms is the multiplicative group $(0, \infty)$ , acting by multiplication. For each $t \in (0, \infty)$ , the automorphism $t\cdot -$ of $V$ induces an automorphism of $V\text{-}Cat = MetSp$ , namely scaling by a factor of $t$ . Thus, for each metric space $A$ and positive real number $t$ , you get a new space $t A$ .

Contrast other common enriching categories. $Set$ has no nontrivial automorphisms, and nor does $Ab$ as far as I’m aware. For $Vect$ , I think you just have automorphisms induced by automorphisms of the ground field, which isn’t very interesting in this context because it doesn’t change dimension. $Cat$ has one (taking the opposite), but that’s not very exciting either because it doesn’t change Euler characteristic. So the resulting categories of enriched categories ( $Cat$ , $Ab\text{-}Cat$ , $Vect\text{-}Cat$ , and $2Cat$ respectively) do not come equipped with interesting scaling-type automorphisms.

The second special feature of our situation is that $\mathbb{R}^n$ is scale-invariant. By that I mean that $t \mathbb{R}^n$ is isometric (i.e. isomorphic as an enriched category) to $\mathbb{R}^n$ , for each $t$ . The isomorphism is canonical once you’ve chosen an origin for $\mathbb{R}^n$ : just scale towards or away from it. So, given a (convex, if you like) subset $A \hookrightarrow \mathbb{R}^n$ , you get a new (convex) subset $t A \hookrightarrow t \mathbb{R}^n \cong \mathbb{R}^n.$ This tells us that $Aut(V) = (0, \infty)$ acts on the set of valuations. Indeed, given a valuation $\phi: \{convex subsets of \mathbb{R}^n\} \to \mathbb{R}$ and $t \in (0, \infty)$ , we can define a new valuation $\phi t$ by $(\phi t)(A) = \phi(t A)$ (for convex $A \subseteq \mathbb{R}^n$ ).

Hadwiger’s theorem tells us that the vector space of valuations has a basis consisting of one homogeneous valuation of degree $d$ for each $d = 0, 1, \ldots, n$ . The significance of the numbers $0, 1, \ldots, n$ is that they are the “eigenvalues” (or something like that) of the action just mentioned. What I mean is this: for each $d \in \mathbb{R}$ , there is a “ $d$ -eigenspace” consisting of all the valuations $\phi$ that are homogeneous of degree $d$ , that is, $\phi t = t^d \phi$ for all $t \in (0, \infty)$ . When $d \in \{0, 1, \ldots, n\}$ , the $d$ -eigenspace is $1$ -dimensional. For all other real values of $d$ , the $d$ -eigenspace is $0$ -dimensional.

So ultimately, the sequence $0, 1, \ldots, n$ parametrizing the various intrinsic volumes comes from the rich automorphism group of $([0, \infty], \geq, +, 0)$ and the scale-invariance of $\mathbb{R}^n$ . To find similar behaviour in other enriched-categorical settings, you’d need a $V$ with plenty of automorphisms and a $V$ -category that was unchanged (up to isomorphism) under the base change induced by any automorphism of $V$ . I don’t know of any interesting situations where that occurs, except in metric spaces. If anyone can think of one, I’d definitely like to know.

Posted by: Tom Leinster on September 6, 2011 5:22 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I don’t think it’s going to work.

I’m glad I asked as that’s a very interesting answer. At the risk of continuing my losing streak, has there been any thought to enrich in $MetSp$ itself? I take it $MetSp$ has some interesting automorphisms via scaling. I don’t know whether it’s possible to emulate your second special condition, a particular $MetSp$ -enriched category with scale invariance.

Hmm. If a metric space is an enriched category, why isn’t $MetSp$ better seen as a bicategory? Then $MetSp-Cat$ could be seen as enrichment in a bicategory?

A cursory search found a couple of papers, here (section 3) and here, exploring categories with metric space-like hom sets.

Posted by: David Corfield on September 7, 2011 10:17 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

has there been any thought to enrich in MetSp itself?

Yes. I know of this reference, for example:

P. America, J. Rutten, Solving reflexive domain equations in a category of complete metric spaces. J. Comp. Syst. Sci 39 (1989), 343-375.

I haven’t read it; I just saw it cited in a paper I was reading. According to that, America and Rutten prove some results on the existence of terminal coalgebras in such categories, which I guess could be viewed as a categorification of theorems on the existence of fixed points.

You can talk about the magnitude of a MetSp-enriched category, using the general definition given in this post, provided that everything’s suitably finite/compact.

I take it MetSp has some interesting automorphisms via scaling.

Yes. This was one of the points I was trying to make in my last comment. Each automorphism $t \cdot -$ of $[0, \infty]$ induces an automorphism of $[0, \infty]\text{-}Cat = MetSp$ , also called $t\cdot -$ . That’s a general categorical phenomenon: a map $V \to W$ of monoidal categories induces a functor $V\text{-}Cat \to W\text{-}Cat$ . Concretely, if $A$ is a metric space then $t A$ is $A$ with its distances scaled up by a factor of $t$ .

I don’t know whether it’s possible to emulate your second special condition, a particular MetSp-enriched category with scale invariance.

Here’s one: $(\ell_p^n, +, 0)$ , for your favourite value of $p$ . This is $\mathbb{R}^n$ with the metric induced by the $p$ -norm. How is this a MetSp-enriched category? Well, it’s a monoid in MetSp, and therefore a one-object enriched category. The relevant tensor product on MetSp is the tensor product of $[0, \infty]$ -enriched categories, which is what you might call the $\ell^1$ product:

$d_{X \otimes Y}((x, y), (x', y')) = d_X(x, x') + d_Y(y, y').$

A monoid in MetSp is a metric space $X$ together with a distance-decreasing map $m: X \otimes X \to X$ , and a unit, satisfying the usual axioms. For $m$ to be distance-decreasing turns out to be equivalent to it being distance-decreasing in each argument separately. So in the case of $+: \ell_p^n \otimes \ell_p^n \to \ell_p^n$ , we’re asking that for each $x \in \ell_p^n$ , the map

$y \mapsto x + y$

from $\ell_p^n$ to itself is distance-decreasing. And it clearly is.

Posted by: Tom Leinster on September 7, 2011 5:18 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Some idle thoughts from a long train journey. If there were a quintessential $MetSp$ -enriched category, analogous to $\mathbb{R}^n$ as a metric space or $[0, \infty]$ -category, I guess one wouldn’t opt for a monoid in $MetSp$ . How about $MetSp$ itself, or $MetSp^n$ ?

Also, given that in the case of $\mathbb{R}^n$ as a metric space, the objects are endowed with more than they need as metric space, e.g., coordinates, why not look at the kind of 2-spaces we should soon see in the Klein 2-geometry thread? E.g., a bundle with a nice (metric?) space as base, then hom objects trivial except for the fibres, $hom(x, x)$ , which could be monoids in metric spaces.

Oh, there was that thread on Weinstein’s volume of a differentiable stack.

Posted by: David Corfield on September 10, 2011 8:36 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

I’m not sure I’ve really stopped to think about this before, but it’s really not obvious how you make Buffon’s needle problem precise, is it?

I don’t think it is, and furthermore I’ve always been dissatisfied with the standard interpretation (location and angle are independent, location in the direction perpendicular to the lines is uniformly distributed in whichever region the needle lands in). Assuming the parallel lines are vertical, we clearly don’t care about the $y$ -coordinate of (say) the center of the needle. But I’ve always felt that assuming the $x$ -coordinate is uniformly distributed modulo the line spacing is poorly motivated. If I really do drop a needle over a lined sheet of paper, it’s very unlikely this will be the case. Consider in particular if the lines are very widely spaced, and I drop a short needle from a small distance above the paper, close to the midpoint between two of the lines. (It’s not clear that the angle of the needle should be independent of the $x$ -coordinate either.)

You could make the case that since the statement of the problem doesn’t give any information about that, the standard interpretation is the most reasonable one on information-theoretic grounds (e.g. maximizing entropy). But the problem is usually stated so as to give the impression that you’re not meant to think about it (the statement) that hard.

Posted by: Mark Meckes on September 2, 2011 4:10 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Here’s a silly toy model. Consider an idealized classical rigid rod of some length, moving in a 2+1 Galilean space-time, perhaps interacting in a perfectly elastic way with the walls of a box (maybe we take the walls to be ice). Then perhaps Buffon’s problem asks how often — that is, what fraction of the time, for generic orbits — are the ends of the rod separated by how many of some family of lines.

This model is meant to simplify a particular method of performing Wolf’s experiment, in which you take several boxes of identical nails and suddenly disperse them (in 3+1 Galilean space-time) in large room with hardwood flooring, which nails are interrupted at random times (how long it takes to reach the floor) and rigidly flattened to a 2-dimensional state. Then you have your graduate student pick up the nails, keeping a careful tally of how many nails meet how many floor-boards. I do realize that the landing times shouldn’t be uniformly distributed, but they ought to be close enough, relative to the periods of rotation and board-crossing.

In particular, however, as stated for a single generic orbit, it does seem that the right probability distrubition should have uniform horizontal position of the centroid and uniform distribution of angles, mutually independent, at least in the limit of a very short needle and proportionally narrow floor boards — or a very large room.

Posted by: some guy on the street on September 5, 2011 9:19 PM | Permalink | Reply to this

Re: Mixed Volume

I have a copy of Klain and Rota’s book (picked up, I think, while I was an undergraduate browsing through the maths section of a local bookshop) and at the time found their merry use of random things hard to follow. At the time I chalked it up to ignorance, and haven’t picked up the book for about 10 years, so it’s interesting to read that there are technical issues that need addressing. As well as my ignorance, of course.

Posted by: Yemon Choi on September 2, 2011 1:23 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Those are good and thought-provoking questions, Mike! You already have a really nice answer from Mark (including that gem of a deduction of the isoperimetric inequality). But I’ll add some other points.

I don’t suppose that might mean that the Hausdorff metric is the wrong topology to put on non-convex regions?

It’s worth noting that the Hausdorff metric has a very natural categorical explanation. (This is in Taking categories seriously too.) Fix a metric space $A$ , which we’re going to view as a $V$ -category with $V = [0, \infty]$ . The functor $V$ -category $[A, V]$ is, concretely, the set of distance-decreasing functions $A \to [0, \infty]$ with the sup metric, and the Yoneda embedding $A^{op} \to [A, V]$ sends $a$ to $d(a, -)$ .

Now take a subspace $X$ of $A$ . Each $x \in X$ gives rise to the representable $d(x, -)$ , and we can define $d(X, -): A \to V$ to be their colimit over all $x \in X$ : concretely,

$d(X, a) = \inf_{x \in X} d(x, a).$

(This is, if you like, a familially representable functor — a coproduct of representables. The representing family is $(x)_{x \in X}$ .)

This defines a function

$\{subspaces of A\} \to ob[A, V],$

sending $X$ to $d(X, -)$ . (Maybe it’s best to cut down to closed subspaces, since then this function is injective: we recover $X$ from $d(X, -)$ as the fibre over $0$ .)

But $[A, V]$ is a metric space, so this makes the set of subspaces of $A$ into a metric space too. It’s a non-symmetric version of the Hausdorff metric. (The Hausdorff metric is blatantly a symmetrized version of something: just look at the definition.) To put it another way, if you replace the non-symmetric metric space $V = [0, \infty]$ by its symmetrization $V_{sym}$ (the usual real half-line), then the distance between the elements $d(X, -)$ and $d(Y, -)$ of $[A, V_{sym}]$ is precisely the Hausdorff distance between $X$ and $Y$ .

Minkowski sum looks kind of unmotivated to me when thinking about “volume”.

I’m not going to address quite that point, but I can say something about why Minkowski sums seem natural when thinking about convexity. Namely: a subset $A \subseteq \mathbb{R}^n$ is convex (or empty) if and only if

$(\lambda + \mu) A = \lambda A + \mu A$

for all $\lambda, \mu \geq 0$ (if and only if the same is true for all $\lambda, \mu \geq 0$ satisfying $\lambda + \mu = 1$ ). So convexity can be interpreted as distributivity.

And (aha!) the nullary version of this law —

$0 A = \{0\}$

— holds if and only if $A$ is nonempty. This is another hint that $\emptyset$ should not be counted as convex.

Can you extend the definition of mixed volume to polyconvex sets in a consistent way (i.e. not depending on the decomposition into convex sets)?

I don’t know. Presumably we’d want to do it so that the multivaluation property (12) holds for all polyconvex $\tilde{A}_1, A_1, \ldots, A_n$ . That would determine any such extension uniquely, but as you say, consistency is the question. I know an extension theorem giving necessary and sufficient conditions for the extension to be possible, but I don’t know whether those conditions are satisfied in this case.

Posted by: Tom Leinster on August 30, 2011 5:01 PM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

It’s worth noting that the Hausdorff metric has a very natural categorical explanation.

That’s very nice! And you mentioned in your other post that convexity also has a categorical explanation (though not, seemingly, one which excludes the empty set). But does volume?

This is, if you like, a familially representable functor — a coproduct of representables

Since this $V$ is a poset, is there any difference between a coproduct of representables (familially representable) and a colimit of representables (any presheaf)?

Posted by: Mike Shulman on August 31, 2011 4:45 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Mike wrote:

you mentioned in your other post that convexity also has a categorical explanation (though not, seemingly, one which excludes the empty set). But does volume?

I don’t know of a genuinely categorical explanation of volume. Here’s one that I think is quite conceptual, though. It’s a result characterizing volume of compact convex subsets of $\mathbb{R}^n$ , up to scale factor. You can easily derive it from Hadwiger’s theorem, although in fact it’s often used as a stepping stone on the way to proving Hadwiger’s theorem.

Here it is. I’ll explain the unexplained terminology in a moment.

Theorem The simple continuous invariant valuations on compact convex subsets of $\mathbb{R}^n$ are precisely the scalar multiples of volume.

Now I’ll go through the various terms in this statement (not in order), examining them for conceptual well-motivatedness and defining them where necessary.

Convex subsets. As you point out, I mentioned a categorical explanation in my other post. There’s actually a second categorical explanation, also due to Lawvere, which I’ll put in a comment over there.
Valuation. A valuation on convex subsets of $\mathbb{R}^n$ is a real-valued function $\phi$ defined on such sets, satisfying $\phi(\emptyset) = 0$ (assuming here that $\emptyset$ counts as convex…) and $\phi(X \cup Y) = \phi(X) + \phi(Y) - \phi(X \cap Y)$ whenever $X$ , $Y$ and $X \cup Y$ are convex. To me, the most puzzling thing here is the extra condition that $X \cup Y$ is convex. This is a reason to work with the class of polyconvex sets, which is closed under unions by definition.
Invariant means invariant under self-isometries of $\mathbb{R}^n$ , which is surely natural.
Continuous refers to the Hausdorff metric on closed subsets of $\mathbb{R}^n$ , which we’ve already discussed.
Simple: a valuation $\phi$ on convex sets is simple if $\phi(X) = 0$ whenever $X$ has dimension $\lt n$ . That in turn means that $X$ has empty interior, or equivalently that $X$ lies in the image of some (not necessarily linear) isometry $\mathbb{R}^{n - 1} \to \mathbb{R}^n$ . Those are both quite hands-on definitions of ‘dimension $\lt n$ ’.

So, judge for yourself how conceptual that is. Note that there’s nothing about countable unions (which you might expect for a statement about measures). Also, you could replace the condition ‘simple’ by ‘homogeneous of degree

n

’, if you found that more natural.

Since this $V$ is a poset, is there any difference between a coproduct of representables (familially representable) and a colimit of representables (any presheaf)?

Good point. I should really have said ‘familially represented’. That is, I was referring to how the functor was constructed rather than any properties it might have. The thought was that I wasn’t using any relationship between the elements $x$ of $X$ ; I was just treating it as a set. So it seemed natural to think of it as a coproduct.

Actually, I think at root I don’t have a clear understanding of how to view closed subsets categorically. Since any closed $X \subseteq A$ gives rise to the $V$ -presheaf $d(-, X)$ , the closed subsets of $A$ can be described as the zero-sets of presheaves on $A$ , or as the regular subobjects of $A$ in $V$ -Cat. But I don’t know whether either of those descriptions is really helpful.

Posted by: Tom Leinster on September 1, 2011 6:02 AM | Permalink | Reply to this

Re: Mixed Volume

$MathML-enabled post (click for more details).$

Thanks! That’s certainly somewhat conceptual. I was asking about a categorial interpretation because I was looking for some intuition that would put the Hausdorff metric and volume in the same context, so that I could get some idea of why it might make sense to compare sets with the Hausdorff metric when what we are interested in is their volume. I don’t think I get that from this characterization of volume, although it’s certainly nice to know!

Posted by: Mike Shulman on September 6, 2011 6:33 PM | Permalink | Reply to this

Read the post Universal Measures
Weblog: The n-Category Café
Excerpt: Groemer's integral theorem recast as a universal property.
Tracked: September 14, 2011 2:20 AM

Read the post Universal Measures
Weblog: The n-Category Café
Excerpt: Groemer's integral theorem, recast as a universal property.
Tracked: May 31, 2021 10:32 PM

The n-Category Café

Skip to the Main Content

August 26, 2011

Mixed Volume

Posted by Tom Leinster

Examples of mixed volume

Minkowski’s theorem

The definition of mixed volume

The unique characterization

Further properties of mixed volume

Some Related Entries

59 Comments & 2 Trackbacks

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Is there some version of Hadwiger’s theorem?

Re: Is there some version of Hadwiger’s theorem?

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Re: Mixed Volume

Access Keys: