The n-Category Café

What is this groupoid that secretly underlies the Hall algebra? To get it, first we take our Dynkin diagram and draw arrows on its edges. We call this a ‘quiver’… because now it’s a picture of a category, and you must be quivering with anticipation to see what’ll happen next.

The next thing we do is look at representations of our quiver on finite-dimensional vector spaces over $\mathbb{F}_q$, the finite field with $q$ elements. This is how the beloved ‘$q$’ of quantum group theory gets into the game!

A ‘representation’ of a quiver is a simple thing: it’s just a vector space for each dot of our quiver, and a linear map for each arrow. Or, if you think of a quiver as a category, a representation is a functor from the quiver to the category of vector spaces.

There’s an obvious notion of a map between quiver representations, which you can surely guess if you understood the previous paragraph. So we get a category of quiver representations. If our quiver is called $Q$, let’s call this $Rep(Q)$.

At this point you should really spend a month going through examples to see what $Rep(Q)$ is like. We had a little seminar at UC Riverside where we did just that. You should work out the indecomposable representations, and the irreducible ones, and study short exact sequences of representations. You’ll see this is a fascinating subject… and you’ll see why the simply-laced Dynkin diagrams are special: these are the ones that give quivers with finitely many indecomposable representations! If you want some help, try these nice notes:

• Andrew W. Hubery, Ringel–Hall algebras.
• Olivier Schiffman, Lectures on Hall algebras.

All the ideas I just mentioned make heavy use of noninvertible maps between quiver representations. But then we can throw out all the maps except the invertible ones. We’re left with a groupoid of representations: let’s call this $Rep(Q)_0$. This is the groupoid that secretly—or perhaps not-so-secretly—underlies the Hall algebra.

Degroupoidification is a process that turns groupoids into vector spaces. The basic idea is pathetically simple: we just take our groupoid, look at its set of isomorphism classes of objects, and use that as the basis for a vector space! But the interesting part is not how any groupoid gives a vector space. It’s how any span of groupoids gives a linear operator between vector spaces. A ‘span’ of groupoids looks like this: $$\begin{matrix} &&S&\\ &\swarrow& &\searrow&\\ Y&& &&X\\ \end{matrix}$$ where $X,Y$ and $S$ are groupoids and the arrows are functors. This sort of gadget gives us a linear operator from the vector space associated to $X$ to the one associated to $Y$. (Or vice versa: the charm of spans is that they’re symmetric.)

I explained how this works back in This Week’s Finds, and we described it more thoroughly here:

• John Baez, Alex Hoffnung and Christopher Walker, Higher-dimensional algebra VII: groupoidification.

We won’t need the details now, if you can take my word for it: all sort of basic linear algebra stuff can also be done with spans of groupoids, but whenever you like you can snap your fingers, ‘degroupoidify’, and turn them into linear operators.

In particular, the Hall algebra gets a multiplication from this span of groupoids: $$\begin{matrix} &&SES(Rep(Q))_0&\\ &p\swarrow& & \searrow q&\\ Rep(Q)_0&&&&Rep(Q)_0 \times Rep(Q)_0 \\ \end{matrix}$$ Here $SES(Rep(Q))$ is the category of short exact sequences of quiver representations, and again the little subscript $0$ means we take the underlying groupoid, where we throw out all the morphisms except isomorphisms. Given a short sequence of quiver representations $$0 \to N \to E \to M \to 0$$ the functor $$p : SES(Rep(Q))_0 \to Rep(Q)_0$$ picks out the representation $E$ in the middle, while the functor $$q: SES(Rep(Q))_0 \to Rep(Q)_0 \times Rep(Q)_0$$ picks out the representations $M$ and $N$ at the two ends.

Since we get the Hall algebra by degroupoidifying $Rep(Q)_0$, any quiver representation gives a basis vector in the Hall algebra. And what I’m saying above basically amounts to this: to multiply the basis vector coming from $M$ by the basis vector coming from $N$, we take a sum over all representations $E$ that fit into a short exact sequence $$\begin{matrix} 0 &\to& N &\to& E &\to& M &\to& 0 \\ \end{matrix}$$ This sum has coefficients that need to be chosen just right, but degroupoidification takes care of that automatically! When we degroupoidify $Rep(Q)_0$ we get the Hall algebra, and degroupoidifying the above span gives its multiplication.

Similarly, we get the comultiplication in the Hall algebra by degroupoidifying the turned-around span $$\begin{matrix} &&SES(Rep(Q))_0&\\ &q\swarrow& & \searrow p&\\ Rep(Q)_0 \times Rep(Q)_0 &&&&Rep(Q)_0 \\ \end{matrix}$$

Now, at first glance, the multiplication and comultiplication in the Hall algebra don’t obey the equation we need to get a Hopf algebra:

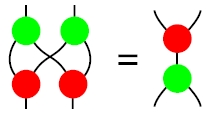
where the green blob is the multiplication and the red blob is the comultiplication. However, this condition involves a braiding: in the diagram at left, one wire needs to cross over the other! It turns out that the Hall algebra becomes a Hopf algebra very neatly if we choose the right braiding. Otherwise we need to do a bunch of ad hoc mucking around, which is what most people do. Christopher explained this here:

• Christopher Walker, Hall algebras as Hopf objects.

The trick is not to work in the category of vector spaces with its usual braiding, but the category of $K$-graded vector spaces with a carefully chosen braiding. What’s $K$? It’s the ‘Grothendieck group’ of $Rep(Q)$: that is, the abelian group with a generator for each quiver representation, and a relation $$E = M + N$$ for each short short exact sequence $$\begin{matrix} 0 &\to& N &\to& E &\to& M &\to& 0 \\ \end{matrix}$$ The Hall algebra is naturally a $K$-graded vector space, since each quiver representation gives a basis vector for the Hall algebra, but it also gives an element of $K$, which we take to be that basis vector’s grade.

The category of $K$-graded vector spaces is a braided monoidal category in a very nice way, which Christopher describes in the paper above. But in fact, like so much about Hall algebras, this idea really wants to be explained at the level of groupoids rather than vector spaces! In his thesis, instead of working with $K$-graded vector spaces, Christopher works with groupoids over $Rep(Q)_0$: that is, groupoids equipped with a functor to the groupoid of quiver representations, like this: $$\begin{matrix} X\\ \downarrow \\ Rep(Q)_0 \\ \end{matrix}$$ Any such groupoid gives, not just a vector space, but a $K$-graded vector space. Why? Because any object of $X$ gives a basis vector of the degroupoidification of $X$, and the grade of that basis vector comes from the corresponding object down below in $Rep(Q)_0$.

Christopher’s main result is that groupoids over $Rep(Q)_0$ form a braided monoidal bicategory in a nontrivial and interesting way. Snapping our fingers and degroupoidifying, this explains why $K$-graded vector spaces form a braided monoidal category! For the details you should read his thesis, notably Chapter 4.

But to whet your appetite, I’ll say that a key idea is to consider $EXT(M,N)$, the groupoid of extensions of $M$ by $N$, where $M$ and $N$ are quiver representations. This has short exact sequences $$\begin{matrix} 0 &\to& N &\to& E &\to& M &\to& 0 \\ \end{matrix}$$ as objects, and diagrams like this: $$\begin{matrix} 0 &\to& N &\to& E &\to& M &\to& 0 \\ & & \downarrow && \downarrow & & \downarrow & & \\ 0 &\to& N &\to& E' &\to& M &\to& 0 \\ \end{matrix}$$ as morphisms. There’s a concept of cardinality for groupoids, and the cardinality of $EXT(M,N)$ is related to the so-called ‘Euler form’ $$\langle M, N \rangle = dim(Hom(M,N)) - dim(Ext^1(M,N))$$ More precisely, $$|EXT(M,N)| = \displaystyle {\frac{q^{-\langle M, N \rangle}}{|Aut(M)| \, |Aut(N)| } }$$ The bilinearity of the Euler form is crucial to making $K$-graded vector spaces into a braided monoidal category… but this bilinearity emerges from properties of $EXT(M,N)$ that are precisely what Christopher needs to make groupoids over $Rep(Q)_0$ braided monoidal bicategory!

And $Rep(Q)_0$ lives in this bicategory, because it’s a groupoid over itself in an obvious way: $$\begin{matrix} Rep(Q)_0\\ \downarrow \\ Rep(Q)_0 \\ \end{matrix}$$ where the vertical arrow is the identity morphism.

At this point, the obvious conjecture is that $Rep(Q)_0$ is a ‘Hopf 2-algebra object’ living in the braided monoidal bicategory of groupoids over $Rep(Q)_0$. Due to the pressure of time, Christopher hasn’t proved this yet. But at this point it’s almost a foregone conclusion. He has the multiplication and comultiplication on $Rep(Q)_0$, and also the unit and counit. He’s shown these degroupoidify to give the Hall algebra as a Hopf object in the braided monoidal category of $K$-graded vector spaces. So, he just needs to check the Hopf 2-algebra axioms.

But he also needs a job!