A Hopf Algebra Structure on Hall Algebras
Posted by John Baez
My student Christopher Walker is groupoidifying Hall algebras. What’s a Hall algebra? We get such an algebra starting from any category with a sufficiently well-behaved concept of ‘short exact sequence’. In this algebra, the product of an object and an object is a cleverly weighted sum over all objects that fit into a short exact sequence
The ‘clever weighting’ is neatly explained by groupoidification, as sketched here. And if we pick our category in a nice way, the algebra we get is part of a quantum group!
But the Hall algebra is more than a mere algebra. It’s also a coalgebra! The algebra and coalgebra want to fit together to form a Hopf algebra, and they do, but only after a peculiar sort of struggle. Lately Christopher has been thinking about this, and he’s written a paper:
-
Christopher Walker, A Hopf algebra structure on Hall algebras.
Abstract: One problematic feature of Hall algebras is the fact that the standard multiplication and comultiplication maps do not satisfy the bialgebra compatibility condition in the underlying symmetric monoidal category . In the past this problem has been resolved by working with a weaker structure called a ‘twisted’ bialgebra. In this paper we solve the problem differently by first switching to a different underlying category of vector spaces graded by a group called the Grothendieck group. We equip this category with a nontrivial braiding which depends on the - grading. With this braiding, we find that the Hall algebra does satisfy the bialgebra condition exactly for the standard multiplication and comultiplication, and will also become a Hopf algebra object.
Comments, anyone? Corrections?
The point is that a Hopf algebra is a bialgebra, so the multiplication and comultiplication need to get along nicely. As we’ve recently discussed, they need to obey a condition sort of like this:
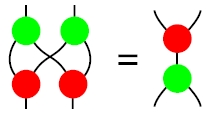
where the green blob is the multiplication and the red blob is the comultiplication. And this condition involves a braiding: in the diagram at left, one wire needs to cross over the other! It turns out that the Hall algebra becomes a Hopf algebra very neatly if we choose the right braiding. Otherwise we need to do a bunch of ad hoc mucking around.
Actually, in the picture above, you’ll note that the two wires just cross, without one visibly going over the other. That style of drawing is fine if we’re in a symmetric monoidal category, like the category of vector spaces with its usual tensor product and usual braiding. But the Hall algebra becomes a Hopf algebra in a braided monoidal category that’s not symmetric. So we need to draw the compatibility condition a bit more carefully — see Christopher’s paper.
All these ideas can be groupoidified, and that’s what Christopher is doing now.

Re: A Hopf Algebra Structure on Hall Algebras
Hi Chris. I just had a quick look at your paper over breakfast.
My first question is about your equation for the set on p4 (equation numbers would be helpful here!). Won’t its cardinality be the continuum in general? Also, I have some typographical comments: I think the distinction between the two types of P is too subtle, something like might be better for the cardinality; also, in the line beginning “and we call” after the displayed equation, you’re missing some punctuation.
Does all this generalize to other quivers which aren’t simply laced?