Pictures of Modular Curves (III)
Posted by Guest
guest post by Tim Silverman
Welcome back to this series of posts: Pretty Pictures of Modular Curves
The Story So Far
The last two times, we started looking at the curves , that is, the quotients of the upper half of the complex plane by the groups , the latter being defined as those subgroups of which consist of the matrices congruent to mod . We discovered that for , and , the resulting quotients (to be strictly accurate: once we have compactified by cusps) can basically be thought of as (the surfaces of) Platonic solids, respectively the tetrahedron, cube and dodecahedron, perhaps best thought of as the spherical versions of those solids. These are curved surfaces tiled regularly with a finite number of regular -gons, with of the tiles meeting at each vertex. This view in terms of tiling also works for the case, which involves a tiling by bigons. The residual action of on these quotient surfaces is then precisely the symmetry of the tiling.
Non-Positive Curvature
Having done the cases and , it’s time to move to . Of course, we can’t fit together regular hexagons on a sphere; we need a (globally) flat surface. The case is a tiling of a torus by hexagons (or, dually, by triangles). However, rather than suffering the pain and confusion of trying to embed a tiled torus in -space and then project it onto the plane for your viewing pleasure, I shall instead tile the whole plane with hexagons, and let the labelling by reduced fractions show how to identify different hexagons in order to take the quotient. I think, in any case, that this is more perspicuous.

Hexagons: N = 6
Actually, letting the numbers do all the work is a bit cruel, so to help make the quotient clearer, I’ll pick out a particular “unit cell” of hexagons so the repeat pattern is obvious.

12 distinct hexagons: N = 6
As you can see, by glancing at the picture, or by looking more carefully at where repeats occur, the repetition actually gives the lattice.
Even with these guidelines, it’s a lot harder to see what’s going on here than it is in the case of the spherical Platonic solids. You might enjoy trying to see the patterns in the fractions here. In any case, I’ll be discussing how they are organised in a lot more depth next time.
Now we can move on to the case . By now, we need the curvature to be negative. As with the flat case, I’ll handle this by tiling the entire hyperbolic plane, and use the repetition of fractions to the indicate the quotient. I’m far too lazy to try to embed the multi-holed compact quotient surface in -space (with its tiling!)—and besides, this has already been done, far better than I could manage, by Greg Egan, Mike Stay and Gerard Westendorp. (In fact, Gerard Westendorp’s page is full of beautiful and cool things relevant to this post, including many superb pictures, so do check it out!)
(I have to admit I’m slightly trepidatious about making this choice, because this surface is the famous Klein Quartic, and I have the impression that people have been expecting me to expound its wonderful properties. Well, maybe some time, but not here, because in this place I’m just slipping it into its place the parade of modular curves, and ignoring things that make it stand out. Sorry about that.)

I’ll again pick a “unit cell”, bordered by thickened edges, and unfortunately annoyingly large.
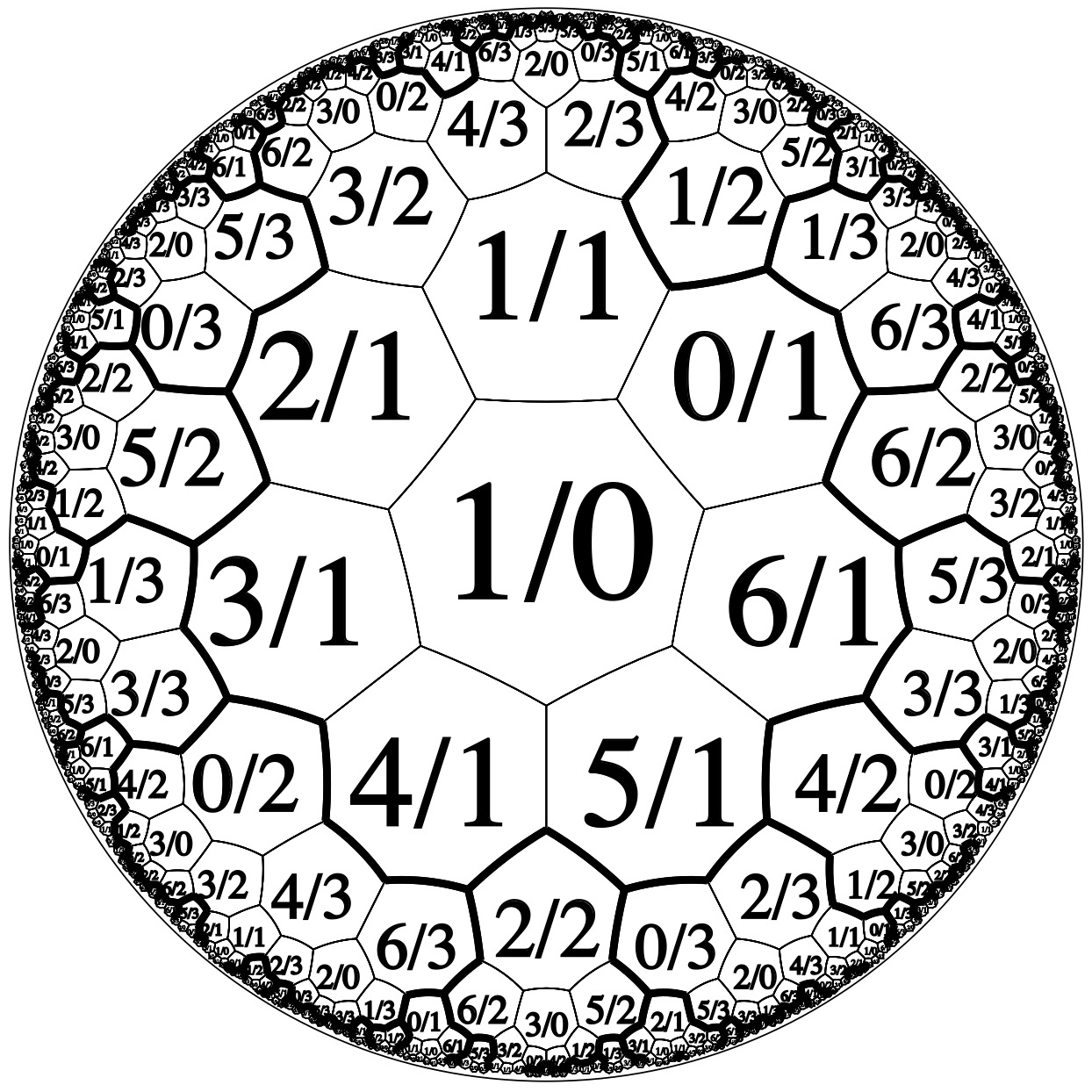
Heptagons: N = 7
Or this might be slightly clearer, putting in the centre instead of .

Heptagons around 1/1: N = 7
Next time, we’ll be looking at more ways to make it clearer what’s going on in here.
Here’s
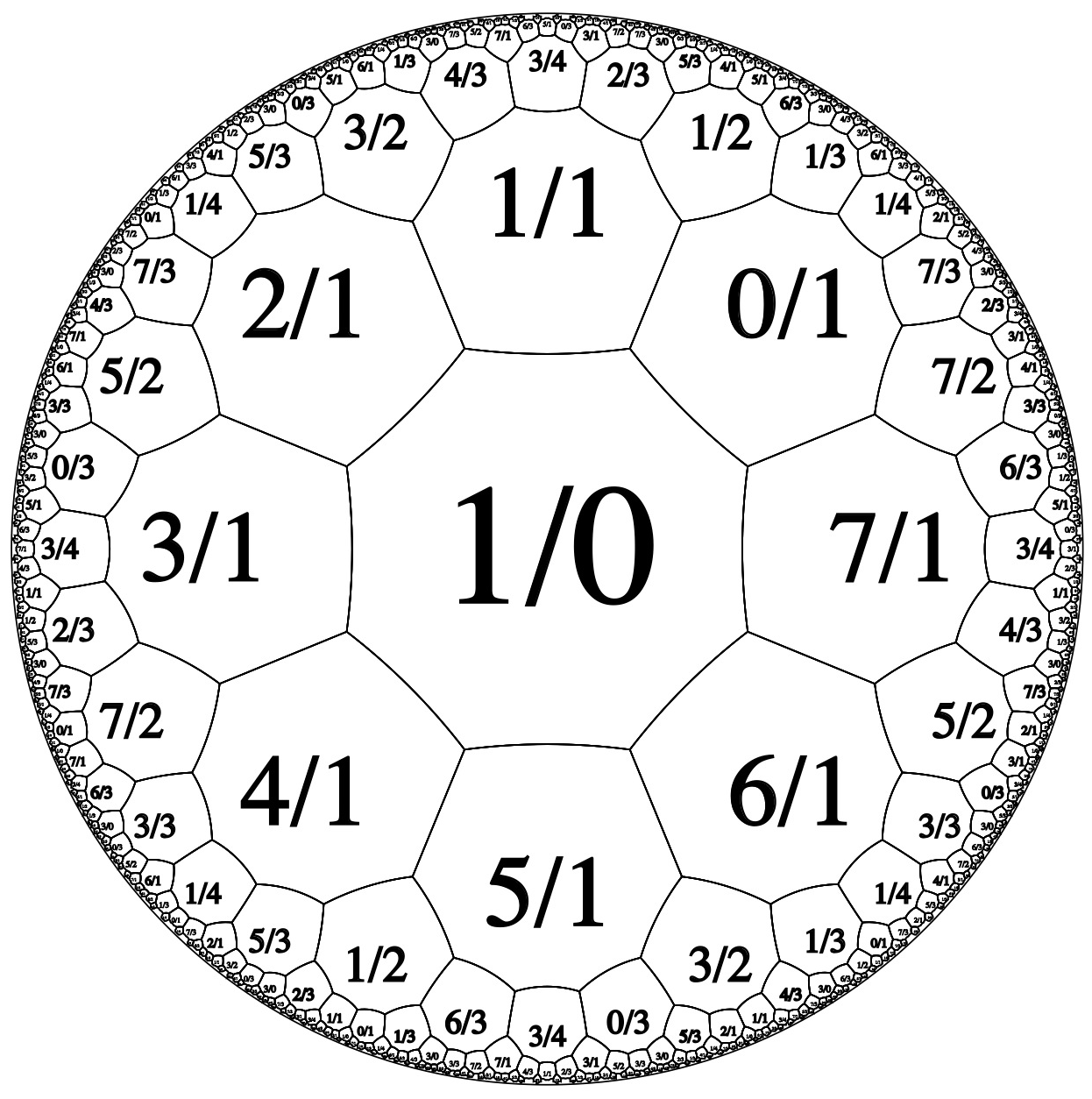
Octagons: N = 8
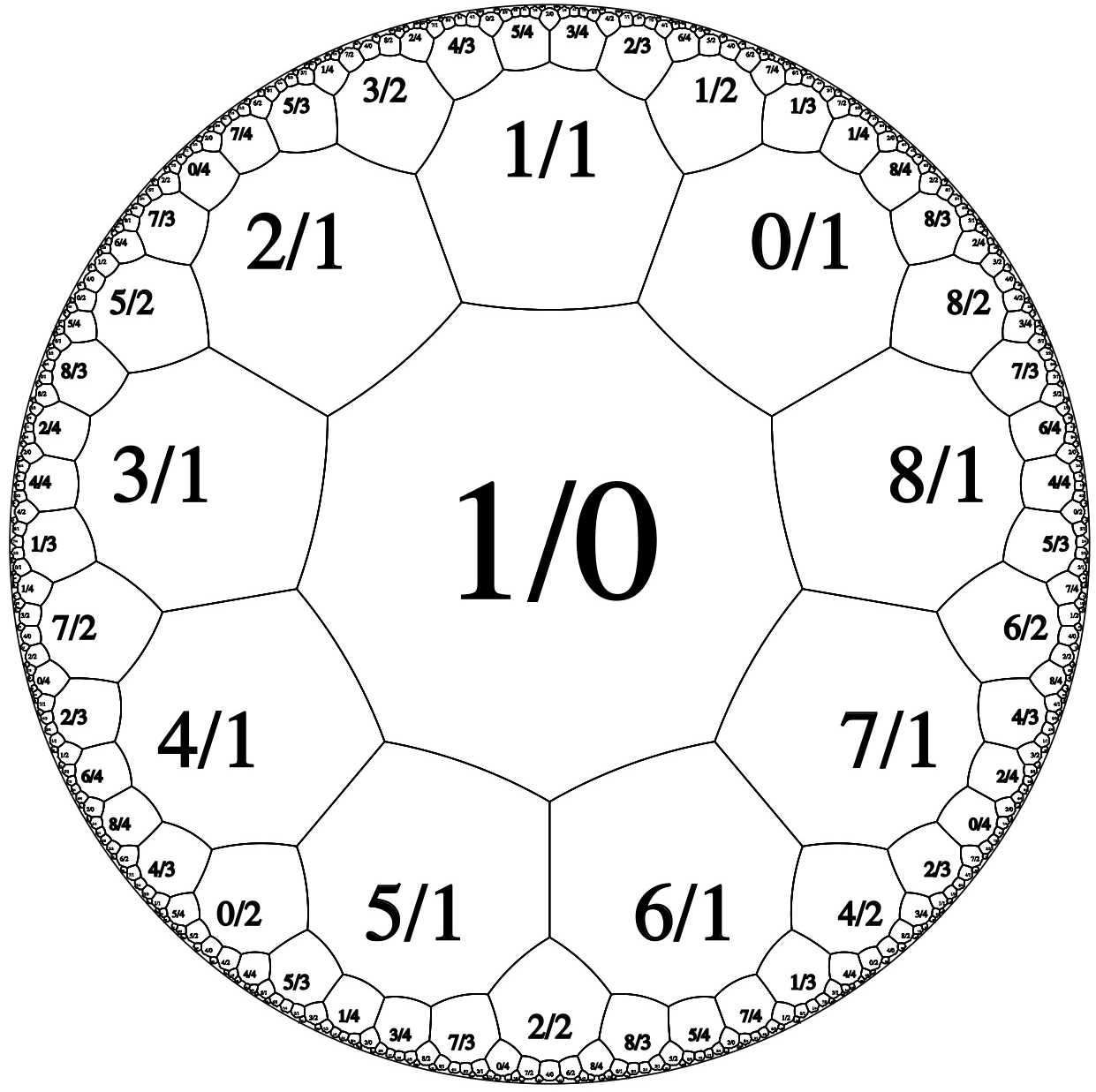
Enniagons: N = 9

Pentadecagons: N = 15
Another view of

Pentadecagons, vertex centred: N = 15
And finally up to , although I guess this could equally well be called , since we are quotienting by the zero ideal in .
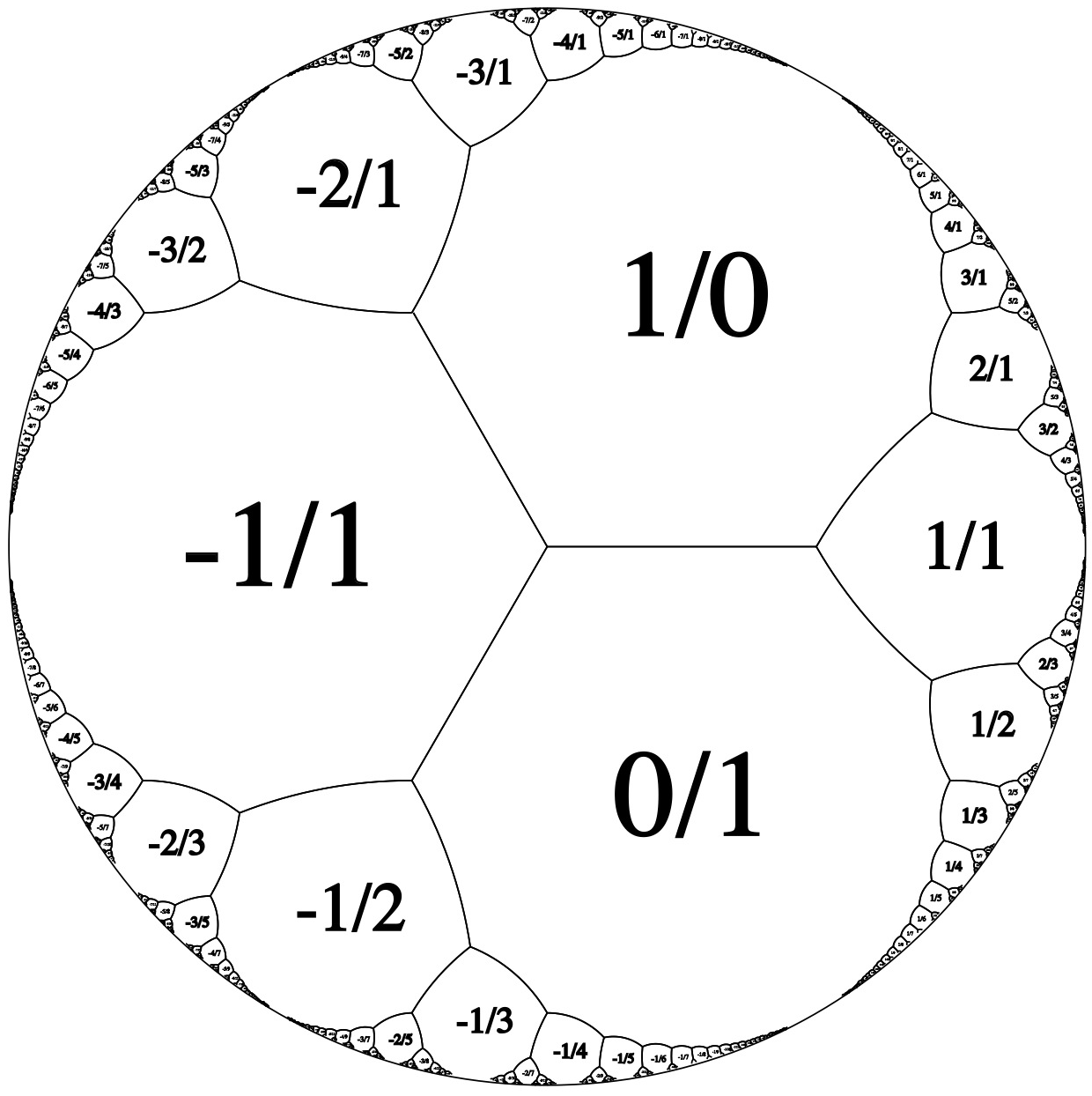
Horocycles: N = infinity
We’ve now gone from regular -gons to what we might call regular -gons or regular -gons. Their incircles are what are sometimes called horocycles.
And for good measure, I’ll finish up where I started in the last post, with the dual of that last picture:

Triangles: N = infinity
I’ll add a couple of notes about this picture and the previous one while I’m about it. Although we’ve been talking largely about the rational numbers and their reductions mod , the interior of the Poincaré disk here is secretly intended to represent not just any old random hyperbolic plane but the upper half of the complex plane, with the circumference representing the real line. Having the metric is undoubtedly nice for drawing and tesselating, but ultimately we’re more concerned with the complex structure. Anyway, if we imagine the Poincaré disks in the last couple of pictures as sitting over the unit disk in the complex plane, then we can see them as images of the complex upper half-plane by taking the latter and applying the transformation , where is the complex cube root of unity which lies in the upper half plane. Then the rationals end up at the points indicated around the circumference. The incircles of the -gons in the above picture are, I believe, the images of the famous Ford circles in the upper half of the complex plane.
Well, having shown you the full range of pictures, I suppose this would be as good a place as any to stop for a break. As usual, I’ve taken far more space than I expected to, and said much less than I intended to. I think I’m about half way through the article as originally planned. We haven’t even reached what I considered the most exciting part of it, where we get to take out our felt-tips and colour things in!—and where we attempt to herd the milling multitude of mod--reduced fractions into some sort of orderly system by staring very hard at their denominators.
Ah well. That’ll be something to talk about next time.


Re: Pictures of Modular Curves (III)
Bravo!
I’m a bit confused about a phenomenon that seems to first show up (at least in this post) in the case N = 7:
How come you’re counting 0/2 and 0/3 as different from 0/1? Aren’t they all just zero, even if we work mod 7?
(With some work I could probably figure out what’s going on, but I figure some other people will have the same question but be too shy to ask it — so in my role as ‘class clown’, I’ll just blurt it out.)