Pictures of Modular Curves (IV)
Posted by Guest
guest post by Tim Silverman
Well, here we are again, trying to understand modular curves in the simplest possible way. The last couple of times, I displayed lots of pictures, and talked about tilings. This time, I’m going to display better pictures—with colour!—and I’m going to talk about denominators. Denominators? Yes, denominators: those things on the bottom of fractions.
Why? Well, we want to understand a little bit more about how the -gons are patched together—not so much topologically as from as a number-theoretical point of view (though that’s a rather grandiose phrase for some mostly simple arithmetic). I also want to look at some larger groups of transformations than just . And I’m going to explore this by considering particularly the denominators of the mod--reduced fractions.
Striping by Denominator
The crude reason that this seems as though it might be worth considering runs roughly like this: we can layer the fractions in Farey sequences into rows by denominator, like this:
We might very crudely represent this as a series of stripes labelled by denominator.
Denominator bands
Adding to all fractions is a symmetry of the triangulation which shifts everything to the right within its own band (so the bands are preserved by a non-trivial subgroup of the symmetry group, helping us partially break down the full complexity).
Moving over to the situation mod , the numbers wrap around, so the bands become circles:
Denominator bands mod N
Now obviously this picture is an oversimplification—the denominators will repeat mod as you move out, the bands are sometimes broken up and partly interleaved, etc—but some pictures will show how it works in practice (SVG makes overlapping translucent colours look a bit strange to my eye, but that’s what’s happening in the pictures below, if you were wondering. The matches of colours to denominators are the same as in the simplified bands above.)
N = 2: coloured by denominator
N = 3: coloured by denominator
N = 4: coloured by denominator
N = 5: coloured by denominator
Well, perhaps that’s not perfectly clear, because of the way SVG handles translucent colours—here’s a version of the last one with a front face removed to show that faces with denominator are really all green.
N = 5: coloured, 0/1 removed
A couple more.

N = 6: coloured by denominator
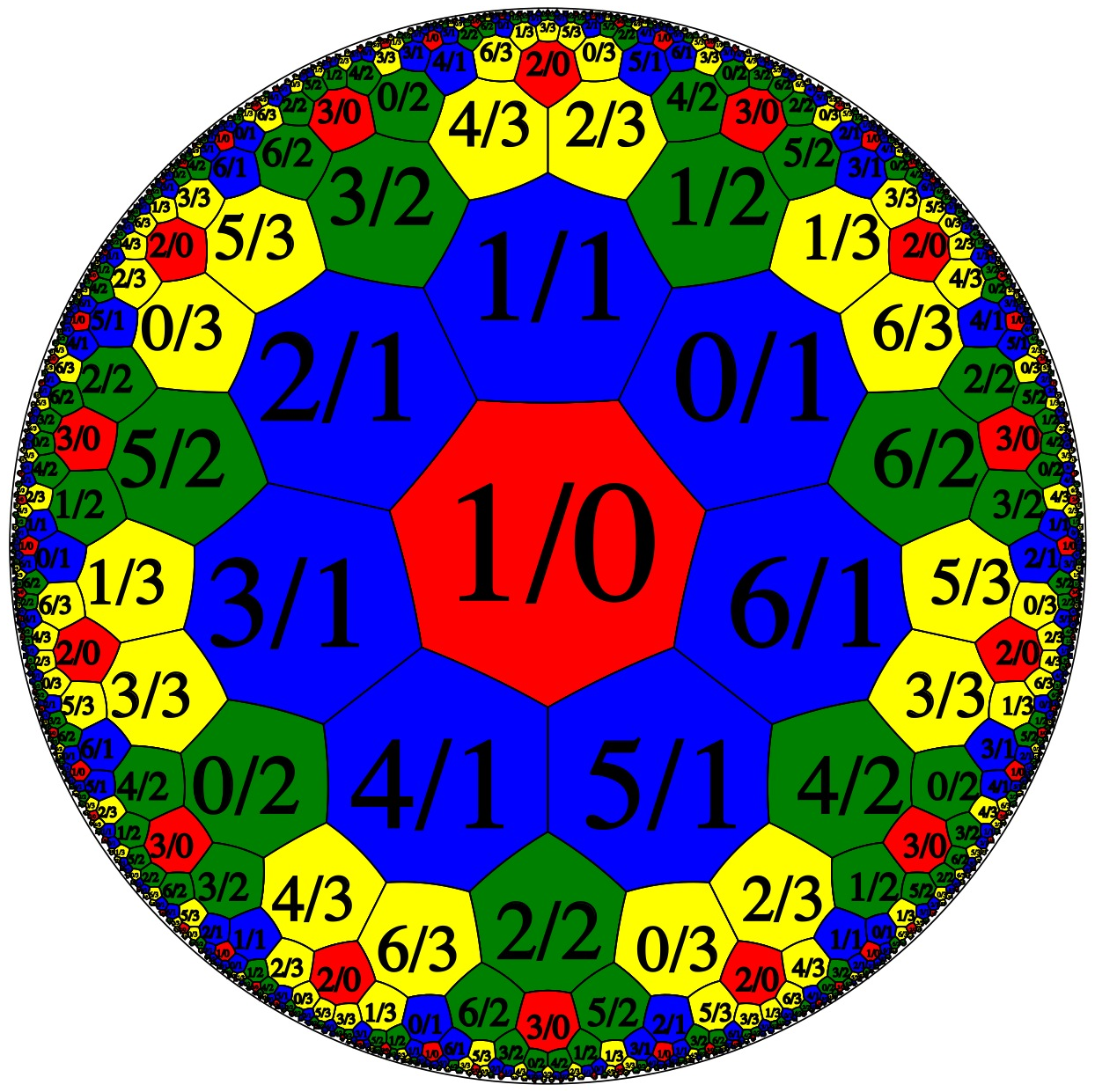
N = 7: coloured by denominator
Supposing this is not completely unhelpful, I want to talk in more detail about organising the tiling by denominator, this time looking at arithmetic aspects a little more carefully.
Translations
First of all, what symmetries of the tiling will preserve denominators? A matrix in will act on a fraction to give . Hence if we want the denominator to still be after the transformation (regardless of what and are), we require and . The requirement that the determinant must also be then forces also. So we are dealing with matrices of the form , where can be anything. Since the product is , this is a subgroup isomorphic to the additive group in . We can think of these as the translations (mod ) of the projective line over —the matrix adds to everything (mod ).
Of course, translations over are cyclic— a kind of rotation, about the centre at . But notice that, setting , we get , whatever is. Not only do these transformations act as rotations around , they also act as rotations around for any other unit !
This fact makes it look as though the different fractions with denominator might be equivalent to each other under some interesting group of symmetries. And this is so, although they are not quite as equivalent as we might think at first, since although rotations about one of them are the same as rotations about the others, the rotations about different centres generally occur at different speeds!
Affine Transformations
So, in pursuit of this idea of going beyond organising the surface into concentric rings by denominator, let us investigate the relationship between different centres of rotation.
We can start by considering a more general group of transformations that respect denominators, namely those that, though they may send a fraction with one denominator to a fraction with a different denominator, nevertheless ensure that two fractions which share the same denominator get sent to fractions which still share a denominator. For this, we only require (so a denominator gets consistently sent to ), so this subgroup consists of the matrices of the form , or (to give a more specific notation) for general , and . However, the requirement of determinant forces , so these latter elements must actually be units of , and reciprocal to each other. In particular, we have a smaller subgroup within this one, consisting of matrices of the form . Since we have , this subgroup is isomorphic to the multiplicative group (of units) in , mod , and we might consider it the “rescalings” mod . The full subgroup might then be considered the “affine transformations” mod . Note also the following: if the denominator , then we have . This is not only the condition we originally wanted (these points are the “centres of rotation”) but also agrees with our description of these transformations as “affine”, since fractions with denominator might be considered to be points “at infinity”, and these transformations keep these points at infinity, as we expect from affine transformations.
So to summarise: the translations, , which preserve denominators, are a subgroup of the group of affine transformations, , which preserve the relation of having the same denominator. The latter is generated by the translations together with the scalings, .
Extending
Now the usual procedure when looking at these groups is to start with (i.e. matrices of the form mod ), and then first to extend by translations, giving (i.e. matrices of the form mod ), and then to extend to the full group (i.e. matrices of the form mod ). And indeed, in due course, I will be following this path. But before I start extending by translations, I want to have a preliminary discussion of its extension by rescalings (i.e. matrices of the form mod ), and talk about the action of rescalings on ; the reason is that that I think the action is easier to understand if we haven’t first quotiented out by translations.
So at this point I want to look into the action of the group of rescalings.
However, there is a limit to how much text the blogging software (not to mention my readers) can swallow at one go, so I think I will leave that for next time.

Re: Pictures of Modular Curves (IV)
Man, I never thought I’d be the only person posting to the nCafé for five days at a stretch. Is the entire rest of the world at a conference in a remote underground cavern with no phones, or something? Should I be stocking up on canned food?