The n-Category Café

Curvatures and the Tube Formula for surfaces in $\mathbb{R}^3$

I will start with the very basics of the notion of curvature of curves and surfaces, then get on to explaining Weyl’s Tube formula. All of this generalizes to arbitrary submanifolds of arbitrary Euclidean spaces, but I’ll stick with this most basic example today.

My standard references for this are the following books:

• J-M Morvan, Generalized Curvatures, Springer Verlag (2008).
• A Gray, Tubes, Birkhauser (2004).

Both are extremely interesting, but both I find flawed in some way, and both are quite notation heavy. Anyway, let’s get on with the story.

Suppose we have a surface $\Sigma$ smoothly embedded in $\mathbb{R}^3$ we want to define some notion of curvature at each point.

What we start with is knowing how to define the curvature of a planar curve, namely if we have a point on a curve then there is a circle in $\mathbb{R}^2$ (perhaps of infinite radius!) which best approximates the curve at that point, this is called the osculating circle at that point. Clearly the smaller the circle, the more curved the curve is at that point, and the curvature at that point is defined to be the reciprocal of the radius this osculating, or best-approximating, circle.

Now back to our surface. If we have a point $x$ on the surface $\Sigma$ then there is a well defined normal line to $x$, and we can decide that one of the two normal directions is going to be positive. Picking a direction on the surface at $x$ will give us a plane spanned by that direction and the normal. The intersection of the surface with this plane is locally a curve and the curvature of $\Sigma$ at $x$ in the given direction is defined to be the curvature of this curve. Here is a picture of the osculating circle corresponding to a direction on a surface.

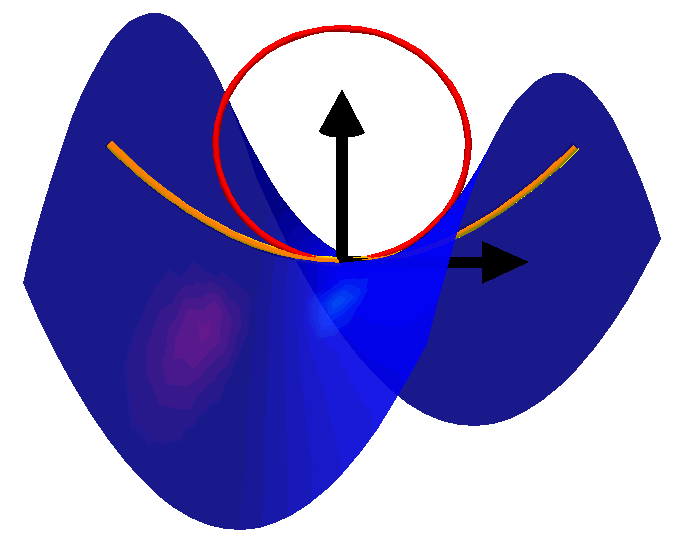
The black arrows are the chosen positive normal and the direction we are interested in. The orange curve is a curve in the surface which is tangent to our specified direction and the red circle is the osculating circle, or circle which best fits the curve. So the curvature of the surface in the shown direction is the reciprocal of radius of the red circle.

We will give the curvature a positive sign if the osculating circle is on the opposite side to the positive normal direction and negative otherwise. Thus in the above picture the given direction has negative curvature, but as the direction is changed at the indicated point, the curvature will become positive. So for each direction in the surface at $x$ we have a signed curvature. The principal curvatures, $\kappa_1$ and $\kappa_2$, at $x$ are taken to be the maximum and minimum values of the curvature. From these we can define the following two invariants at $x$:

• Gauss curvature $K(x):=\kappa_1\kappa_2$;
• mean curvature $H(x):=(\kappa_1+\kappa_2)/2$.

Although these look to be of the same nature, they have quite different properties. At a basic level you can see that if you switch the chosen normal direction then the principal curvatures will both switch signs, so Gauss curvature is independent of the choice of normal direction, but the sign of the mean curvature depends on the choice of normal direction. More generally, the Gauss curvature is intrinsic meaning that if you are an ant living on the surface then you can find out the Gauss curvature by just making measurement on the surface, whereas the mean curvature is not intrinsic.

We will see why the latter is true in a minute, but first I will tell you how to measure the Gauss curvature of the Earth on which you are living. The idea is that you measure the circumference of the circle consisting of all points on the Earth a distance $r$ away from a fixed point. If you were on a plane then the circle would be of length $2\pi r$, but because the Earth is (approximately) spherical the circle will have a smaller circumference than that. For small $r$ the deficit in the circumference is to first approximation given by the Gauss curvature:

$$Circumference = 2\pi r\left( 1- \frac{K(x)}{6}r^2+O(r^4)\right).$$

and this determines the Gauss curvature at that point. For instance, it is an exercise in high-school geometry to show that on a radius $R$ sphere the circumference of a radius $r$ circle is

$$2\pi R sin\tfrac{r}{R}=2\pi r \left(1- \tfrac{1}{6R^2}r^2+O(r^4)\right)$$

so the Gauss curvature of the radius $R$ sphere is $1/R^2$ at every point. This should not be surprising as you can see straight away that the principal curvatures at every point are both $1/R$ (the osculating circle is always a great circle on the sphere).

I could have equally well talked about the deficit in the area of a disc of radius $r$ and expressed that to first approximation in terms of the Gauss curvature. The moral of this is that if you have a goat tied to a post on a fixed length rope then the more positive the Gauss curvature of the field is, the less grass the goat will have to eat!

The fact that the Gauss curvature is intrinsic to the surface is known as Gauss’ Theorema Egregium, or Remarkable Theorem.

I should now point out why the mean curvature is not intrinsic. Consider a piece of paper. If the piece of paper is flat then the principal curvatures are all zero, so the mean curvature is zero. If you roll the piece of paper into a cylinder of radius $r$ then at each point the principal curvatures are $0$ and $1/r$ so the mean curvature is $1/2r$. However if you were an ant living on the piece of paper then none of your intrinsic measurements would be able to distinguish the two situations – the lengths and angles of things are not changed. Thus the mean curvature is not an intrinsic invariant. As the Gauss curvature is an intrinsic invariant it ought to be the same in both cases, and indeed it is just zero each time.

The next remarkable thing about the Gauss curvature is the Gauss-Bonnet Formula which says that if you have a closed surface then when you integrate Gauss curvature then you obtain, up to scale, one of the most fundamental invariants of geometry and topology – the Euler characteristic – remember that for an orientable surface the Euler characteristic is just related to the “number of holes” or genus $g(\Sigma)$ by $\chi(\Sigma)=2-2g$.

Gauss-Bonnet Formula. For an oriented closed surface $\Sigma$ in $\mathbb{R}^3$ the integral of the Gauss curvature is proportional to the Euler characteristic:

$$\int_\Sigma K(x) dx = 2\pi\chi(\Sigma).$$

So, for instance, no matter how you embed a sphere in Euclidean the integral of the Gauss curvature is always going to be $4\pi$: if you make it more positively curved at one point you have to compensate by making it less curved at another point. Similarly if you embed a torus in $\mathbb{R}^3$ then the integral of the Gauss curvature is going to be $0$ so it will have to be positively curved in some places and negatively curved in others.

Now I want to get to the Tube Formula which is a general form is due to Weyl, but the following version for surfaces was undoubtably known before him. The set up is the following. Suppose you have a surface $\Sigma$ embedded in $\mathbb{R}^3$ and we define $N_\epsilon\Sigma$ to be the $\epsilon$-neighbourhood of $\Sigma$, that is all of the points within an $\epsilon$ distance of $\Sigma$. What is the the volume of $N_\epsilon\Sigma$? The answer is perhaps a little surprising the first time you see it.

Weyl’s Tube Formula for a Surface in $\mathbb{R}^3$. For an oriented closed surface $\Sigma$ in $\mathbb{R}^3$, and for $\epsilon$ sufficiently small, the volume of the $\epsilon$-neighbourhood is given by the following formula:

$$vol(N_\epsilon \Sigma)= 2 Area(\Sigma) \epsilon + \frac{4\pi}{3}\chi(\Sigma)\epsilon^3.$$

For the standard embedding of a radius $R$ sphere this is a straight forward calculation as the $\epsilon$–neighbourhood is just a radius $(R+\epsilon)$ 3–ball with a $3$-ball of radius $(R-\epsilon)$ removed (so “$\epsilon$ sufficiently small” here means $\epsilon\lt R$). For a general surface the proof is a one page differential geometry calculation which can be found in the book by Gray. I should point out, to remove any mystery, that the coefficients $2$ and $4\pi/3$ are the volumes of the unit $1$–ball and unit $3$–ball respectively.

The first thing to notice about this is that it is a polynomial in $\epsilon$. The next thing to notice is that the dependency on $\Sigma$ is via integrals of local things on the surface, namely the area, $\int_\Sigma dx$, and the Euler characteristic, $\int_\Sigma \kappa_1\kappa_2/2\pi dx$. The surprising thing is that the expression only depends on intrinsic properties of the surface – it does not depend on the embedding per se.

The analogous thing one dimension down is that if you have a smooth, simple, closed curve $\Gamma$ in the plane then the area of the $\epsilon$–neighbourhood is just

$$Area(N_\epsilon \Gamma)= 2 Length(\Gamma) \epsilon$$

which is independent of the embedding. However, if you just took the inside piece, or the outside piece of the neighbourhood, then you would have got something which would have depended on the curvature of the embedding, but when you add the two bits together then this dependency cancels out.

A similar thing happens with the inside and the outside of the $\epsilon$-neighbourhood of a surface. The contributions which cancel out in that case actually come from the mean curvature – remember we observed that the mean curvature switches sign if you switch your chosen normal direction, well this is related to that phenomenon. [In fact in higher dimensions, to get the tube formula you need to integrate certain curvatures over the unit normal bundle, and the ‘odd’ ones will cancel themselves out, as has happened with the mean curvature here.]

One way to write the Tube Formula for a Surface which will generalize is to write $\omega_i$ for the volume of the unit $i$–ball, and write $\mu_2$ and $\mu_0$ for the area and Euler characteristic respectively, and taking $\mu_3$ and $\mu_1$ to be zero, then for a $2$–dimensional surface in $3$–dimensional space and $\epsilon$ sufficiently small:

$$vol(N_\epsilon \Sigma)= \mu_2(\Sigma) \omega_1\epsilon + \mu_0(\Sigma)\omega_3\epsilon^3= \sum_{i=0}^3\mu_{3-i}(\Sigma) \omega_i\epsilon^i.$$

For arbitrary submanifolds of arbitrary Euclidean spaces you get appropriately generalized Lipschitz-Killing curvatures $\{\mu_i\}$ and a Tube Formula of the above form. I hope to talk about these another time. However, I just want to briefly try to tie this in with intrinsic volumes as described by Tom previously.

Intrinsic volumes and polyconvex sets

Back in his original post on the magnitude of metric spaces (then called the cardinality of metric spaces), Tom described the intrinsic volumes for certain basic subsets of Euclidean space – the finite unions of convex sets, also known as polyconvex sets. For a fixed a Euclidean space $\mathbb{R}^k$ the invariant valuations (or measures in Tom’s terminology) are defined to be the the functions on the set of polyconvex sets which are invariant under rigid motions, which are continuous in an appropriate sense and which are finitely additive, in other words such a function $\mu$ satisfies the inclusion-exclusion principle:

$$\mu(A\cup B)=\mu(A)+\mu(B)-\mu(A \cap B) \qquad for polyconvex A and B.$$

Here are some standard examples:

$$\begin{aligned} \mu_k &= k\text{-dimensional volume}\\ \mu_{k-1} &= \tfrac{1}{2}\text{"surface area"}\\ \mu_{0}&= \text{Euler characteristic} \end{aligned}$$

Hadwiger’s Theorem says that these three invariants can be extended to a basis $\mu_0, \mu_1, \dots, \mu_k$ of all the invariant valuations. The valuation $\mu_i$ is called the $i$th intrinsic volumes and is homogeneous of degree $i$ in the sense that as a subset is scaled up by a factor of $t\gt 0$ then the $\mu_i$ scales up by a factor of $t^i$ – think about the examples above – so $\mu_i(t A)=t^i \mu_i(A)$, where $t A$ means $A$ scaled up by a factor of $t$.

One of the most well-known results involving intrinsic volumes is Steiner’s Formula.

Steiner’s Formula. Suppose that $K$ is a convex subset in $\mathbb{R}^k$, that $N_\epsilon K$ is the set of all points within $\epsilon$ of $K$ and that $\omega_i$ is the volume of the unit $i$-ball, then we have the following formula for the volume of the $\epsilon$-neighbourhood of $K$: $$vol(N_\epsilon K) = \sum_{i=0}^k\mu_{k-i}(K)\omega_i \epsilon^i.$$

If you have not seen this before then you should draw a picture of the $\epsilon$-neighbourhood of a (convex!) triangle in the plane and identify the three terms on the right hand side in the expression for the area of the neighbourhood; namely something involving the Euler characteristic of the triangle(which is $1$!), something involving (half) the perimeter of the triangle, and something involving the area of the triangle.

Steiner’s Formula looks remarkably similar to Weyl’s Tube Formula, but is definitely different. The subspaces that are being considered namely convex sets and closed submanifolds are quite distinct types of space – convex sets are flat with possibly curved, possibly non-smooth boundary; closed submanifolds are curved, smooth and have no boundary. However, there is, of course, a common generalization of these two theorems which I leave you to ponder.

The point is that the intrinsic volumes are actually defined on a considerably greater class of subsets of $\mathbb{R}^k$ which includes both polyconvex sets and submanifolds. This was originally done by Federer in his work on curvature measures but generalized by others since. The book of Morvan goes into details about the history. The relevant fact about the subsets is that they need to have some appropriate notion of unit normal bundle, known as a normal cycle. Moreover, these invariants do seem to crop up in lots of places and be of a fundamental nature.

Of course it remains to be seen quite how much of these invariants are seen by the magnitude of metric spaces.