Division Algebras and Supersymmetry II
Posted by John Baez
John Huerta and I are finishing up another paper:
- John Baez and John Huerta, Division algebras and supersymmetry II.
We’d love comments and corrections! In particular, the material on supergravity theories needs improvement. But the story is already quite cool, since it connects the octonions and higher gauge theory to superstrings, super-2-branes and supergravity.
In case you’re wondering, I don’t “believe in” string theory. But I’ve always been curious about it, since it’s full of interesting mathematics. After I officially quit work on quantum gravity — a subject rife with warring factions — I eventually realized I could relax and do whatever I wanted, without needing to take sides. So, I’ve been slowly trying to learn more about superstrings, supergravity and supersymmetric membranes, as kind of back burner hobby. But it seems the best way to learn a bit about a subject is to do some work on it. So, with John Huerta’s help, I’ve been dipping my toe into this pool. I make guesses; he does the hard work required to prove or disprove them.
I’d always been curious about why supergravity is so quirky when it comes to working in some dimensions and not others. It’s frustrating to hear people wax rhapsodic about, say, 11-dimensional supergravity, when you don’t know what’s so special about 11 dimensions! There are some simple explanations one often hears, but they’re not completely satisfying.
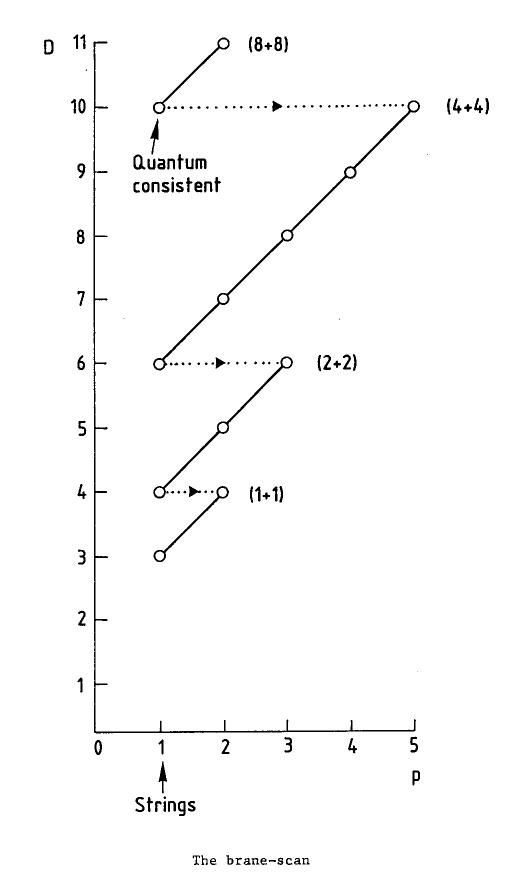
Now I feel happier. I know I’m still just skimming the surface — but it’s nice to see some beautiful mathematical structures that explain why there are classical superstrings in dimensions 3, 4, 6, and 10, and super-2-branes in dimension 4, 5, 7 and 11, as shown in this old chart by Michael Duff, which shows super--brane theories in -dimensional spacetime:
Duff says that the four diagonal lines here come from the four normed division algebras. In our previous paper on this subject, we explained how these algebras, namely:
- the real numbers, of dimension 1,
- the complex numbers, of dimension 2,
- the quaternions, of dimension 4, and
- the octonions, of dimension 8
explain subtle features of the interplay between spinors and vectors in spacetimes of dimensions 3, 4, 6, and 10, respectively. It’s no coincidence that these dimensions are two higher than those of the division algebras! We explained why. And we explained how the mathematics of division algebras leads to an identity involving 3 spinors — an identity that holds only in these dimensions:
We explained how this ‘3-’s rule’ underlies the existence of supersymmetric Yang–Mills theories when spacetime has dimension 3, 4, 6, or 10. It also underlies the existence of classical superstring theories in these dimensions.
None of this was new: we just wanted to explain it clearly, all in one place. Now we’re doing something a bit more novel. We can also use division algebras to prove a fancier rule involving 4 spinors. This ‘4-’s rule’:
holds in spacetimes of dimensions three higher than those of the division algebras: that is, dimensions 4, 5, 7, and 11. And this rule is why there exist supersymmetric 2-branes in these dimensions!
Even better, in the octonionic case — that is, 11-dimensional spacetime — these 2-branes are closely related to 11-dimensional supergravity. In fact, a lot of people expect that 2-branes and supergravity in 11 dimensions are just offshoots of a magnificent, magical, mysterious, murky mess called ‘-theory’.
But our focus in this paper lies elsewhere. In fact, the 3-’s rule and the 4-’s rule are ‘cocycle conditions’.
Let me sketch why this is interesting.
The groups that physicists like all have Lie algebras. Lie algebras show up in particle physics because they describe how particles transform as they move around. But recently people have discovered gadgets called Lie -algebras, which do the same job for strings. And Lie -algebras, which do the same job for 2-dimensional membranes, usually called ‘-branes’. And so on!
In fact, a Lie -algebra is actually a kind of hybrid structure: a blend of a Lie algebra and an -category.
But if you’re a practical sort of person, you may want to build a Lie -algebra starting from some stuff you can easily get your hands on. The simplest way is to start with a Lie algebra and a gizmo called an -cocycle: some sort of function satisfying some equation called a ‘cocycle condition’. From this, you can get a Lie -algebra that includes your original Lie algebra.
All stuff has a supersymmetric version, too — a version where we treat bosons and fermions in a unified way!
In particular, the 3-’s rule actually asserts the existence of a 3-cocycle, which lets us build a Lie 2-superalgebra which is useful for superstring theories. And the 4-’s rule asserts the existence of a 4-cocycle, which lets us build a Lie 3-superalgebra which is useful for super-2-brane theories.
What Lie superalgebra do we start with in this game? It’s a very important one, called the ‘Poincaré superalgebra’.
You see, special relativity says we live in Minkowski spacetime. The group of symmetries of Minkowski spacetime is called the Poincaré group. This has a Lie algebra: the Poincaré algebra. And there’s a supersymmetric analogue of all this, starting from ‘super-Minkowski spacetime’. Super-Minkowski spacetime unifies vectors and spinors in a nice way. And the supergroup of symmetries of super-Minkowski spacetime has a Lie superalgebra, called the Poincaré superalgebra.
Super!
The 3-’s rule implies that the Poincaré superalgebra has a nontrivial 3-cocycle when spacetime has dimension 3, 4, 6, or 10.
Similarly, the 4-’s rule implies that the Poincaré superalgebra has a nontrivial 4-cocycle when spacetime has dimension 4, 5, 7, or 11.
So, the 3-’s rule gives Lie 2-superalgebras extending the Poincaré superalgebra in dimensions 3, 4, 6 and 10. We call these superstring Lie 2-algebras, because they appear to be useful in understanding how classical superstrings move around in these dimensions.
Similarly, the 4-’s rule gives Lie 3-superalgebras extending the Poincaré superalgebra in dimensions 4, 5, 7 and 11. We call these 2-brane Lie 3-algebras, because they appear to be useful in understanding how classical super-2-branes move around in these dimensions.
The biggest and best of these gadgets is the Lie 3-superalgebra built using the octonions — the one that governs super-2-branes in 11 dimensions. This was already studied by Sati, Schreiber and Stasheff. They called it sugra(10,1), thanks to the role it plays in 11-dimensional supergravity. Indeed, you can see Urs blogging about these ideas back in 2007, and even earlier, on my birthday back in 2006.
So, what we’re doing now is fitting this gadget into a bigger pattern — a pattern that involves the division algebras. Since I like -categories and I like division algebras, it makes me very happy to see them fitting together this way. In mathematics, everything sufficiently beautiful is related.

Re: Division Algebras and Supersymmetry II
Why don’t arbitrary composition algebras work? What is it about normed division algebras that’s necessary for doing these constructions?