This Week’s Finds in Mathematical Physics (Week 280)
Posted by John Baez
In week280 of This Week’s Finds, hear about the courses taught by Ashtekar and Rovelli at the quantum gravity summer school in Corfu. Ashtekar spoke about loop quantum cosmology, and how it could turn the Big Bang into a Big Bounce. Rovelli spoke about spin foam models, and how the new EPRL model cures many problems of the old Barrett-Crane model. The graviton propagator seems to work!
From the New Scientist:
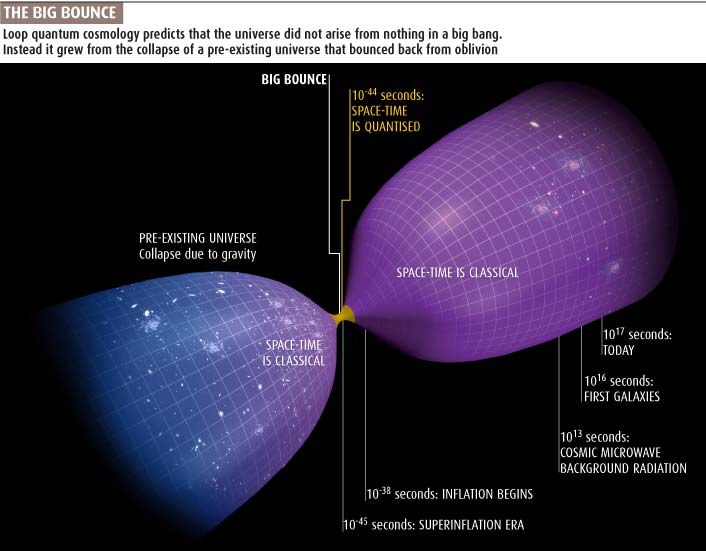
Click on the picture to read the article!
By the way, this picture makes it look like there are galaxies near the Big Bounce in the ‘previous’ universe but not ours. I think a time-symmetrical picture is more likely. See the discussion below…



Re: This Week’s Finds in Mathematical Physics (Week 280)
Welcome back to quantum gravity research! (or at least I suppose that you are interested again…).
Anyway, thanks for the nice summary.
Best,
Christine