Causality in Discrete Models of Spacetime

July 27, 2008

Causality in Discrete Models of Spacetime

Posted by John Baez

$MathML-enabled post (click for more details).$

guest post by Gavin Wraith

Excuse me pestering you with a query about an article in the Scientific American — ‘The Self-Organizing Quantum Universe’ by Ambjörn, Jurkiewicz and Loll. I found the article interesting but frustrating. It gives hints but no definite description of the mathematics involved. The references given were evidently written for a readership of physicists not mathematicians.

$MathML-enabled post (click for more details).$

The diagrams of the article suggested, at least to me, that the Causality Principle meant enriching simplicial complexes (no “semi”) with a partial order on the vertices — i.e. one considers finite subsets of a partial order, closed under intersection. From the language of the article, which talks about dimensions “emerging” from some statistical procedure, I take it that no prior restrictions are made on the simplicial dimension. The barycentric subdivision functor on simplicial complexes extends naturally to the partially ordered case once one defines a simplex $a$ to be less-than-or-equal to a simplex $b$ if every vertex of $a$ is less-than-or-equal to every vertex of $b$ . I could find no clue from the article what the measure on the set of isomorphism-classes of these things was supposed to be.

My ideas are evidently very hazy and naive. The article gives the impression that starting from as little as possible (but what?), the authors manage to produce (but how?) something very like de Sitter space. Does any of this stuff approach any of your purlieus (or should that be purlieux)? Have simplicial complexes plus partial ordering swung into your ken at any point? They seem a natural enough concept, but I have never seen them used in the literature. There used to be a vogue at one time for an axiomatic approach to spacetime, based entirely on time-ordering. Also papers looking at other topologies than the Euclidean on Lorentz space — e.g. say a set is open if every timelike line intersects it in an open interval — for which propagators appear much better behaved. I do not think anything particular came of them.

When it comes to finite models and ambitious programs to get something that resembles spacetime to drop out of “nothing”, i.e. some simply describable mathematical gadget that has not been forged in the crucible of “phenomenology”, my thoughts turn to random graphs. For any type of structure on finite sets you can count the isomorphism classes of structures with $n$ elements, weight each class by the inverse of the number of automorphisms and come up with the probability that a randomly chosen structure belongs to a given class. Then you can start asking how these probabilities behave as $n$ varies. That is where the fun starts. Let us say that a structure type is ‘interesting’ if asymptotically there are only a finite number of isomorphism classes with nonzero probability. So random graphs are definitely interesting in this sense as there is only one such class. That is the sort of scenario I would love to see develop.

Posted at July 27, 2008 12:26 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1751

51 Comments & 0 Trackbacks

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

In reply to Gavin Wraith’s questions, I’ll start by reposting a few of my own summaries of what Ambjörn, Loll and Jurkiewicz have been doing. The first is from week206, written on May 10, 2004, back when I still worked on quantum gravity. It’s part of a report from a quantum gravity conference in Marseille.

I’m delighted to see some real progress on getting 4d spacetime to emerge from nonperturbative quantum gravity:

3) Jan Ambjorn, Jerzy Jurkiewicz and Renate Loll, Emergence of a 4d world from causal quantum gravity, available as hep-th/0404156.

This trio of researchers have revitalized an approach called “dynamical triangulations” where we calculate path integrals in quantum gravity by summing over different ways of building spacetime out of little 4-simplices. They showed that if we restrict this sum to spacetimes with a well-behaved concept of causality, we get good results. This is a bit startling, because after decades of work, most researchers had despaired of getting general relativity to emerge at large distances starting from the dynamical triangulations approach. But, these people hadn’t noticed a certain flaw in the approach… a flaw which Loll and collaborators noticed and fixed!

If you don’t know what a path integral is, don’t worry: it’s pretty simple. Basically, in quantum physics we can calculate the expected value of any physical quantity by doing an average over all possible histories of the system in question, with each history weighted by a complex number called its “amplitude”. For a particle, a history is just a path in space; to average over all histories is to integrate over all paths - hence the term “path integral”. But in quantum gravity, a history is nothing other than a SPACETIME.

Mathematically, a “spacetime” is something like a 4-dimensional manifold equipped with a Lorentzian metric. But it’s hard to integrate over all of these - there are just too darn many. So, sometimes people instead treat spacetime as made of little discrete building blocks, turning the path integral into a sum. You can either take this seriously or treat it as a kind of approximation. Luckily, the calculations work the same either way!

If you’re looking to build spacetime out of some sort of discrete building block, a handy candidate is the “4-simplex”: the 4-dimensional analogue of a tetrahedron. This shape is rigid once you fix the lengths of its 10 edges, which correspond to the 10 components of the metric tensor in general relativity.

There are lots of approaches to the path integrals in quantum gravity that start by chopping spacetime into 4-simplices. The weird special thing about dynamical triangulations is that here we usually assume every 4-simplex in spacetime has the same shape. The different spacetimes arise solely from different ways of sticking the 4-simplices together.

Why such a drastic simplifying assumption? To make calculations quick and easy! The goal is get models where you can simulate quantum geometry on your laptop - or at least a supercomputer. The hope is that simplifying assumptions about physics at the Planck scale will wash out and not make much difference on large length scales.

Computations using the so-called “renormalization group flow” suggest that this hope is true if the path integral is dominated by spacetimes that look, when viewed from afar, almost like 4d manifolds with smooth metrics. Given this, it seems we’re bound to get general relativity at large distance scales - perhaps with a nonzero cosmological constant, and perhaps including various forms of matter.

Unfortunately, in all previous dynamical triangulation models, the path integral was not dominated by spacetimes that look like nice 4d manifolds from afar! Depending on the details, one either got a “crumpled phase” dominated by spacetimes where almost all the 4-simplices touch each other, or a “branched polymer phase” dominated by spacetimes where the 4-simplices form treelike structures. There’s a transition between these two phases, but unfortunately it seems to be a 1st-order phase transition - not the sort we can get anything useful out of. For a nice review of these calculations, see:

4) Renate Loll, Discrete approaches to quantum gravity in four dimensions, available as gr-qc/9805049 or as a website at Living Reviews in Relativity, http://www.livingreviews.org/Articles/Volume1/1998-13loll/

Luckily, all these calculations shared a common flaw!

Computer calculations of path integrals become a lot easier if instead of assigning a complex “amplitude” to each history, we assign it a positive real number: a “relative probability”. The basic reason is that unlike positive real numbers, complex numbers can cancel out when you sum them!

When we have relative probabilities, it’s the highly probable histories that contribute most to the expected value of any physical quantity. We can use something called the “Metropolis algorithm” to spot these highly probable histories and spend most of our time focusing on them.

This doesn’t work when we have complex amplitudes, since even a history with a big amplitude can be canceled out by a nearby history with the opposite big amplitude! Indeed, this happens all the time. So, instead of histories with big amplitudes, it’s the bunches of histories that happen not to completely cancel out that really matter. Nobody knows an efficient general-purpose algorithm to deal with this!

For this reason, physicists often use a trick called “Wick rotation” that converts amplitudes to relative probabilities. To do this trick, we just replace time by imaginary time! In other words, wherever we see the variable “t” for time in any formula, we replace it by “it”. Magically, this often does the job: our amplitudes turn into relative probabilities! We then go ahead and calculate stuff. Then we take this stuff and go back and replace “it” everywhere by “t” to get our final answers.

While the deep inner meaning of this trick is mysterious, it can be justified in a wide variety of contexts using the “Osterwalder-Schrader theorem”. Here’s a pretty general version of this theorem, suitable for quantum gravity:

5) Abhay Ashtekar, Donald Marolf, Jose Mourao and Thomas Thiemann, Constructing Hamiltonian quantum theories from path integrals in a diffeomorphism invariant context, Class. Quant. Grav. 17 (2000) 4919-4940. Also available as quant-ph/9904094.

People use Wick rotation in all work on dynamical triangulations. Unfortunately, this is not a context where you can justify this trick by appealing to the Osterwalder-Schrader theorem. The problem is that there’s no good notion of a time coordinate “t” on your typical spacetime built by sticking together a bunch of 4-simplices!

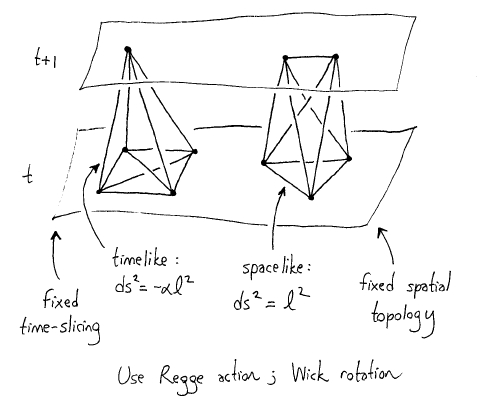
The new work by Ambjorn, Jurkiewiecz and Loll deals with this by restricting to spacetimes that do have a time coordinate. More precisely, they fix a 3-dimensional manifold and consider all possible triangulations of this manifold by regular tetrahedra. These are the allowed “slices” of spacetime - they represent different possible geometries of space at a given time. They then consider spacetimes having slices of this form joined together by 4-simplices in a few simple ways.

The slicing gives a preferred time parameter “t”. On the one hand this goes against our desire in general relativity to avoid a preferred time coordinate - but on the other hand, it allows Wick rotation. So, they can use the Metropolis algorithm to compute things to their hearts’ content and then replace “it” by “t” at the end.

When they do this, they get convincing good evidence that the spacetimes which dominate the path integral look approximately like nice smooth 4-dimensional manifolds at large distances! Take a look at their graphs and pictures - a picture is worth a thousand words.

Naturally, what I’d like to do is use their work to develop some spin foam models with better physical behavior than the ones we have so far. If you look at my talk you can see some of the problems we’ve encountered:

6) John Baez, Spin foam models, talk at Non Perturbative Quantum Gravity: Loops and Spin Foams, May 4, 2004, transparencies available at http://math.ucr.edu/home/baez/spin_foam_models/

Now that Loll and her collaborators have gotten something that works, we can try to fiddle around and make it more elegant while making sure it still works. In particular, I’m hoping we can get well-behaved models that don’t introduce a preferred time coordinate as long as they rule out “topology change” - that is, slicings where the topology of space changes. After all, the Osterwalder-Schrader theorem doesn’t require a preferred time coordinate, just any time coordinate together with good behavior under change of time coordinate. For this we mainly need to rule out topology change. Moreover, Loll and her collaborators have argued in 2d toy models that topology change is one thing that makes models go bad: the path integral can get dominated by spacetimes where “baby universes” keep branching off the main one:

7) Jan Ambjorn, Jerzy Jurkiewicz and Renate Loll, Non-perturbative Lorentzian quantum gravity, causality and topology change, Nucl. Phys. B536 (1998) 407-434. Also available as hep-th/9805108.

Renate Loll and W. Westra, Space-time foam in 2d and the sum over topologies, Acta Phys. Polon. B34 (2003) 4997-5008. Also available as hep-th/0309012.

By the way, it’s also good reading about their 3d model:

8) Jan Ambjorn, Jerzy Jurkiewicz and Renate Loll, Non-perturbative 3d Lorentzian quantum gravity, Phys.Rev. D64 (2001) 044011. Also available as hep-th/0011276.

and for a general review, try this:

9) Renate Loll, A discrete history of the Lorentzian path integral, Lecture Notes in Physics 631, Springer, Berlin, 2003, pp. 137-171. Also available as hep-th/0212340.

Posted by: John Baez on July 27, 2008 1:06 PM | Permalink | Reply to this

Temporal Diffeomorphisms

Since no one else has brought it up, I suppose I shall have to ask the obvious question.

Since we’ve chosen a particular time-slicing, there’s something that we have to check: namely that, in the continuum limit, we recover invariance under temporal diffeomorphisms.

In a canonical formalism, this is known as “imposing the Hamiltonian constraint.” What’s the analogous condition here, and do we know that it’s satisfied?

(Note: there’s a distinction between restricting our path integral to 4-manifolds which admit global foliations by spacelike slices, and choosing one such foliation. It’s the latter that concerns us here.)

Some (now rather old) musings on this point can be found here.

Posted by: Jacques Distler on August 6, 2008 8:14 AM | Permalink | PGP Sig | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

Jacques Distler wrote:

Since no one else has brought it up, I suppose I shall have to ask the obvious question.

Since we’ve chosen a particular time-slicing, there’s something that we have to check: namely that, in the continuum limit, we recover invariance under temporal diffeomorphisms.

I haven’t been following research on quantum gravity for the last few years, but back when I gave that talk in 2005 this was my biggest worry concerning the work of Ambjörn, Loll and Jurkiewicz. The talk transparencies express the concern in its least technical form: “Does causal dynamical triangulations reduce to general relativity as $\ell, \hbar \to 0$ ? Or does the fixed time-slicing mess things up?” Here $\ell$ is the lattice spacing.

If the dependence on the fixed time-slicing is real, we could get all sorts of classical field theories other than general relativity in this limit, and then we’d know we were doing something wrong.

Of course we also want the dependence on the fixed time-slicing to be immaterial in some limit where $\hbar$ remains nonzero; otherwise we could get all sorts of quantum field theories other than quantum gravity in this limit.

This is why I advocated finding models incorporating causal structure, but without a fixed time-slicing.

Posted by: John Baez on August 6, 2008 2:36 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

We know perfectly well that, in classical GR, we cannot restrict to spacetimes which admit global foliations by spacelike slices.

Even in pure gravity, you can start with perfectly smooth initial value data (admitting such a foliation) and, when you evolve it forward in time, horizons form.

If such geometries are explicitly excluded from your path integral, it’s hard to imagine that that path integral reproduces classical GR in some limit.

Posted by: Jacques Distler on August 6, 2008 5:05 PM | Permalink | PGP Sig | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

I can’t resist chiming in during this discussion about time-slicing, etc. I thought it would give me an opportunity to increase my crackpot index by trying to advertise once again my own pet ideas on this issue, which I mentioned many moons ago in this thread.

Inspired by John’s picture above, I thought I’d also make a picture to illustrate what I am trying to say:

Recall how it works: the idea is to set up quantum dynamics as a connection on a vector bundle, in such a way that no time slices are ever needed and hence the theory is manifestly covariant — provided the connection is flat.

One starts with the worldline $\gamma$ of an observer in spacetime $X$ . At each time $t$ along the worldline, consider the collection of vectors orthogonal to the ‘forward’ direction $\dot{\gamma}$ of the observer. By shooting out geodesics from these vectors, we sweep out a submanifold $Z_t = Z_{(x, v_x)} \subset X$ which is what I propose the observer considers to be ‘space’ at that instant.

So at each time $t$ we have a Hilbert space $H_t = L^2(Z_t)$ , and the things that the observer calls ‘wavefunctions’ are really things which live in these Hilbert spaces, i.e. $\psi(t) \in H_t$ .

The observer doesn’t realize this of course: he just thinks there is one fixed Hilbert space $H$ and that all his dynamics takes place in that space. But globally, what is going on is that the Klein-Gordon/Dirac equation is really a connection on this bundle of Hilbert spaces over the tangent bundle on spacetime, and he is simply ‘sampling’ that part of it which his worldline cuts through.

In this language, relativistic invariance amounts to the requirement that the connection is flat: so that if two stationary observers stand together and both paint a picture of The World, then the one runs around the block while the other remains still, then when the second returns he should paint the same picture as the first guy.

I have moved on since I last brought this up: I am more confident there is some truth to what I am saying, because of the rigorous path integral formula for the heat kernel as developed by Bar and Pfaffle which I/we discussed here (see also “example 2.16” of Stolz and Teichner).

In the path integral formalism, the kernel for going from $a$ to $b$ is given by integrating over all paths $\sigma(t)$ from $a$ to $b$ in $X$ such that $\sigma(t) \in Z_t$ for all $t$ . This is the condition that from the observer’s perspective, the particle doesn’t vanish off the face of the map, so to speak :-)

Posted by: Bruce Bartlett on August 6, 2008 5:44 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

Bruce was

trying to advertise once again [his] own pet ideas on this issue, which [he] mentioned many moons ago in this thread.

I think this is a pretty good description of quantum mechanics on a pseudo-Riemannian background. Often people are content with playing this game using a fixed folitation by spacelike slices, which in your picture corresponds essentially to concentrating on just a single fixed timelike curve. What you point out is that there is a nice picture even if we allow that curve to vary.

Yes, sounds good. Maybe an slight issue with geodesic completeness and closed geodesics, but in essence this looks good.

But notice that the discussion in this thread has been about something a bit different: it’s about not QM on a fixed background geometry, but about doing the path integral for gravity itself.

Posted by: Urs Schreiber on August 6, 2008 6:57 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

Maybe an slight issue with geodesic completeness and closed geodesics, but in essence this looks good.

Ok thanks. Yes I admit there is an issue with the things you mentioned.

But notice that the discussion in this thread has been about something a bit different: it’s about not QM on a fixed background geometry, but about doing the path integral for gravity itself.

Yes sorry you’re right; I was a bit confused. Quantum gravtiy is a different story. I think there might be a general principle to what I am saying though, which bears weight even in a quantum gravity context. Namely, “no dynamics without worldlines”. I am uncomfortable with approaches to quantum gravity which speak about the “time evolution of the metric” but don’t mention a wordline.

Anyhow, I’m secretly one of those who believes we still have a lot to learn about basic quantum mechanics, not to mention GR, and that once we “see the light” and change our paradigms we’ll find quantum gravity all magically slips into place.

Funnily enough, I learnt GR in a course given by Renate Loll.

Posted by: Bruce Bartlett on August 7, 2008 12:48 AM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

Jacques Distler wrote:

We know perfectly well that, in classical GR, we cannot restrict to spacetimes which admit global foliations by spacelike slices.

Every globally hyperbolic spacetime admits a global foliation by spacelike slices. I believe these include all the spacetimes for which we have experimental evidence. If I had Hawking and Ellis’s book at my disposal, or Wald’s, I’d do a quick check.

Even in pure gravity, you can start with perfectly smooth initial value data (admitting such a foliation) and, when you evolve it forward in time, horizons form.

That’s true. But it’s not in contradiction with global hyperbolicity: there are plenty of spacetimes where black holes form, which admit a foliation by Cauchy surfaces. You just have to let the Cauchy surfaces move forwards slowly in some places. There’s a lot about this in the GR books mentioned above.

But, even without any horizons around, if your Cauchy surface advances forwards at constant lapse, nasty stuff can happen — for example, it can crash into itself. Caustics! So, there are lots of things to worry about here….

And this is just one of many reasons I enjoy not thinking about quantum gravity, and plan to continue.

Posted by: John Baez on August 6, 2008 10:31 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

But, even without any horizons around, if your Cauchy surface advances forwards at constant lapse, nasty stuff can happen — for example, it can crash into itself. Caustics! So, there are lots of things to worry about here….

Isn’t CDT, essentially by construction, a theory of constant lapse metrics (a point that I was carelessly eliding, above)?

Posted by: Jacques Distler on August 6, 2008 11:02 PM | Permalink | PGP Sig | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

Jacques wrote:

Isn’t CDT, essentially by construction, a theory of constant lapse metrics (a point that I was carelessly eliding, above)?

Yes, if by ‘constant lapse metric’ we mean a Lorentzian metric $g$ on a manifold $M$ equipped with a time function $t: M \to \mathbb{R}$ whose level surfaces are Cauchy surfaces and the gradient of $t$ has constant length. I’d prefer to call this a ‘metric with constant-lapse time function’.

I think you’re right that the existence of a constant-lapse time function puts unphysical restrictions on the metric $g$ .

But I’ve always been worried about something I consider even more problematic. Instead of a discretized path integral over $g$ , causal dynamical triangulations is more like a discretized path integral $g$ and $t$ .

The set of diffeomorphism-invariant local Lagrangians you can write down with a metric and constant-lapse time function is larger than the set of Lagrangians you can write in terms of just a metric. Ted Jacobson has analyzed these Lagrangians in his work on what he calls Einstein–aether gravity.

Of course, these days few people except crackpots relish the concept of ‘aether’. But Jacobson is no crackpot: he’s just noting that the $t$ field provides a local ‘rest frame’, just like aether was supposed to. In other words, it breaks the local Lorentz group down to the rotation group $SO(3)$ .

Jacobson mutters some words about effective field theory and writes down the most general diffeomorphism-invariant local Lagrangian involving $g$ and $t$ and containing no more than two derivatives. According to him, it contains four extra terms besides the Ricci scalar. This is his action for ‘Einstein–aether gravity’.

I’m worried that causal dynamical triangulations may be a quantization of Einstein–aether gravity. This is why I’d like a similar model that doesn’t have a built-in slicing.

If my worry has been successfully addressed, or I’m just mixed up, I’d love to be corrected by any experts on causal dynamical triangulations reading this.

Posted by: John Baez on August 10, 2008 11:07 AM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

Jacobson mutters some words about effective field theory and writes down the most general diffeomorphism-invariant local Lagrangian involving $g$ and $t$ and containing no more than two derivatives. According to him, it contains four extra terms besides the Ricci scalar. This is his action for ‘Einstein–aether gravity’.

I haven’t looked at Ted’s paper, but the same idea has been extensively explored in recent years under the name of “ghost condensate.” There are many things wrong with the ghost condensate (or, if you will, with Einstein-æther gravity). The most serious being that you can use blackholes in such a theory to build a perpetuum mobile.

Posted by: Jacques Distler on August 10, 2008 4:30 PM | Permalink | PGP Sig | Reply to this

Re: Temporal Diffeomorphisms

Question from the peanut gallery…

Since we’ve chosen a particular time-slicing, there’s something that we have to check: namely that, in the continuum limit, we recover invariance under temporal diffeomorphisms.

I’d be happy to be shown the light, but I don’t see why should this should be a test of any theory.

What if the test of a continuum theory should be how well it recovers the discrete theory as you discretize it? Shouldn’t the true test be how well the theory matches observations? Maybe I’m confused (not unlikely), but the stated challenge seems to carry a very strong bias that the continuum is, in fact, the right theory and anything else should approximate IT. What if the continuum is the approximation to something that is fundamentally discrete?

Posted by: Eric on August 6, 2008 5:16 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

Jacques wrote:

Since we’ve chosen a particular time-slicing, there’s something that we have to check: namely that, in the continuum limit, we recover invariance under temporal diffeomorphisms.

Eric wrote:

I’d be happy to be shown the light, but I don’t see why should this should be a test of any theory.

The point is that general relativity seems to work pretty well, so most people want their theories of quantum gravity to reduce to general relativity in some limit. If causal dynamical triangulations doesn’t meet the test Jacques describes, it might reduce to Einstein–aether gravity rather than general relativity.

This is not necessarily fatal, because Einstein–aether gravity itself has general relativity in a certain limit. But for a physically realistic theory, one would need to show that the ‘aether coupling terms’ are small. In short, ones job would get harder.

The good news is that causal dynamical triangulations is being studied by computer simulations, and eventually people will see what’s really going on.

Posted by: John Baez on August 10, 2008 11:20 AM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

Rather than spending effort trying to prove a nice continuum limit to GR, I’d be more impressed if they simulated two masses and saw them orbit one another as you’d expect from observations.

The continuum limit is overrated and maybe even misguided. A consequence of historical accident rather than anything fundamental. It introduces a bias that I don’t see as being particularly helpful. That is all I’m trying to say.

Posted by: Eric on August 11, 2008 3:41 AM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

What “expectations” are you talking about, if not those that follow from GR?

I’m really unclear what it is, as a practical matter, that you are arguing for as a suitable test for CDT (or whatever your favourite lattice model might be).

Posted by: Jacques Distler on August 11, 2008 4:00 AM | Permalink | PGP Sig | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

What “expectations” are you talking about, if not those that follow from GR?

First, I didn’t say “expectations”. I said “expect from observations”. It is probably not more than a philosophical point, but I don’t think any observation follows from GR. Observations follow from the laws of nature, which GR might approximate, but I think it is clear that GR does not rise to the level of dictating to us what should be observed.

To try to answer your question I think it might help to repeat what I actually said (with emphasis added in bold)

Rather than spending effort trying to prove a nice continuum limit to GR, I’d be more impressed if they simulated two masses and saw them orbit one another as you’d expect from observations.

I meant that we have pretty good reproducible measurements relating to what happens when two massive objects are in the vicinity of one another. These observations are completely independent of GR, i.e. I wouldn’t describe these observations as following from GR. Rather, I would say that GR does a good job of describing (and in some cases) predicting certain observations.

If we had another discrete model that allowed us to simulate the dynamics of massive objects that are in the vicinity of one another, and if these simulations were able to reproduce the observations, then I would say that this discrete model is just as good of a model of nature as GR regardless of whether GR was the continuum limit of the discrete model.

The test of a good model should not be whether GR is contained in the continuum limit. The test of a good model should be how well it is capable of explaining model-independent observations and ultimately its ability to correctly predict things that haven’t been observed yet.

I happen to be of the opinion that a lot of the challenges that physics faces in general are due to the historical accident of introducing the continuum model of spacetime through the use of coordinates. I would go as far as to say that if someone were to develop a good discrete model that explained all observations and successfully predicted observations that hadn’t been made yet AND had GR as a continuum limit, this would be good for GR and pretty irrelevant as far as the discrete model was concerned. Then GR could claim to be the continuum limit of a truer discrete model.

Posted by: Eric on August 11, 2008 9:04 AM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

]I really don’t understand your position, either philosophically, or practically.

I have no idea what it would mean for a theory to reproduce all of the observations in the regime of parameter space where GR has been been observed to be hold, and yet not “reduce to GR” in that regime.

Perhaps there is a semantic distinction that you wish to draw, whose importance I fail to appreciate.

But, otherwise, your point is lost on me.

(To dispell one possible objection, let me point out that a clash of ontologies — by itself — is no barrier to such a reduction. GR reduces to Newtonian Gravity, and QM reduces to Classical Mechanics, in appropriate limits, even though the underlying ontologies are utterly different.)

I’m guessing, however, that this is not worth arguing about, as it hardly impacts the issues John and I have been discussing.

Posted by: Jacques Distler on August 11, 2008 9:01 PM | Permalink | PGP Sig | Reply to this

Re: Temporal Diffeomorphisms

I’m guessing, however, that this is not worth arguing about, as it hardly impacts the issues John and I have been discussing.

I agree 100%. I said what I wanted to say as clearly as I am capable of saying it. Any failure on my part to explain myself demonstrates one of the reasons I’m no longer working in physics :)

Sorry for the distraction.

Posted by: Eric on August 11, 2008 9:44 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

Eric wrote:

Rather than spending effort trying to prove a nice continuum limit to GR, I’d be more impressed if they simulated two masses and saw them orbit one another as you’d expect from observations.

I think you’re taking the term ‘continuum limit’ in a different spirit than Distler or I mean it.

First of all, physicists don’t ‘prove’ stuff like mathematicians do. If you’re imagining some poor slob trying to demonstrate the existence of some limit using a bunch of epsilons and deltas, forget it.

Second, when physicists say a discrete theory of quantum gravity must reduce to general relativity in the continuum limit, most of us simply mean that when you use this theory to make predictions at length scales much larger than the scale at which discreteness kicks in, we should get results that match — or nearly match — the confirmed experimental predictions of GR.

In other words, the theory has to fit the observed data.

Getting bodies to orbit each other correctly would be great!

But in fact it’s too expensive to numerically simulate bodies for an entire orbit. Nobody even knows how to do that for black holes in GR, much less some discrete model of quantum gravity. Most researchers on discrete models of quantum gravity are happy to get an approximate inverse square force law.

For example, that’s what Rovelli has been trying to do in spin foam models. But it’s not called the ‘inverse square force law’ — that sounds too Newtonian. It’s called the correct graviton propagator.

Getting the correct graviton propagator seems easier in theories that don’t destroy local Lorentz invariance by relying on a specific slicing of spacetime by timelike surfaces: symmetry considerations take you a long ways. That’s the kind of reason I’m worried about the preferred slicing in causal dynamical triangulations.

Posted by: John Baez on August 14, 2008 3:22 PM | Permalink | Reply to this

Continuum Limit

$MathML-enabled post (click for more details).$

Thank you for taking the time to clarify that.

To say that a discrete model converges to the continuum model, I always thought of this as meaning the discrete equations converge to the continuum equations in the limit $l\to 0$ . It seems this is different than what you had in mind, so we were probably talking about two different things.

The very meaning of “continuum limit” seems more subtle than it may appear at first.

Posted by: Eric on August 14, 2008 6:05 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

$MathML-enabled post (click for more details).$

Sometimes people think of the ‘continuum limit’ of quantum gravity as one in which the Planck length goes to zero: $\ell_p \to 0$ .

However, it makes little invariant sense to say a dimensionful quantity goes to zero. What’s more important is that some dimensionless ratio $\ell_p/L$ goes to zero. Here $L$ is some other length, e.g. the distance between two black holes in a circular orbit around each other.

We can ask for our theory of quantum gravity to reduce to general relativity as $\ell_p/L \to 0$ . In the absence of any other length scale — for example in a theory of ‘pure gravity’ where there are no massive particles in the theory to provide a length scale — there’s no way to tell whether $\ell_p/L \to 0$ means ‘make the Planck length small’ or ‘make the black holes far apart’.

But in the presence of other length scales — e.g. in our universe, where the Bohr radius of the hydrogen atom gives another length scale — the sensible interpretation of the $\ell_p/L \to 0$ limit is ‘make the black holes far apart’. We want quantum gravity to reduce to general relativity (or something awfully close) in this limit.

It only took me ten years to realize that this is the so-called ‘continuum limit’ everyone was talking about.

Posted by: John Baez on August 14, 2008 6:29 PM | Permalink | Reply to this

Re: Temporal Diffeomorphisms

Minimizing “distance between two black holes in a circular orbit around each other” is a crazy way to connect Schwartzchild radius and radius of elementary particle, which some future genius may achieve in unifying QED and GR, but does not tackle Quantum Gravity as generally conceived. QED demands that, for instance, electron MUST be a point, with no extent in 3-D, no internal structure. Failure to provide a valid Theory of the Electron was called by Einstein one of the hidden problems of modern Physics. Not about Compton wavelength, mind you. QED does break down as one approaches Planck length, but I don’t see how that helps with gravity.

Posted by: Jonathan Vos Post on August 14, 2008 8:49 PM | Permalink | Reply to this

Continuum limit

$MathML-enabled post (click for more details).$

If you want to complete that prescription, you also need to scale the masses of the blackholes. What you want to do is send $\begin{gathered} M/M_{\text{pl}} \to \infty\\ \ell_{\text{pl}}/L \to 0 \end{gathered}$ holding $\frac{M}{M_{\text{pl}}}\cdot \frac{\ell_{\text{pl}}}{L}$ fixed.

Posted by: Jacques Distler on August 14, 2008 10:39 PM | Permalink | PGP Sig | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

The next little summary of Ambjörn, Jurkiewicz and Loll’s work comes from week222, written on October 17, 2005 as part of a report on the quantum gravity conference Loops ‘05. My talk at this conference also included a quick summary of their work.

This picture from my talk should answer some of Gavin’s questions:

What does this picture mean?

In their paper, Ambjörn, Jurkiewicz and Loll consider a fixed 4-manifold with topology $[0,1] \times S$ for some compact 3-manifold $S$ which represents ‘space’. They use the obvious time coordinate on this 4-manifold to define slices of ‘constant time’. Then they use a Metropolis algorithm to randomly roam around triangulations of this 4-manifold such that the 4-simplices get along with the time slicing in the two ways shown above. These 4-simplexes have ‘spacelike’ and ‘timelike’ edges of lengths $\ell$ and $\sqrt{-\alpha} \ell$ , respectively.

To know what we mean by ‘randomly roaming around’ an infinite set, we need to know a finite measure on that set. In the Metropolis algorithm, the measure on the set of triangulations is counting measure weighted by $exp(-S)$ , where $S$ is a function called the ‘Regge action’. To compute $S$ , we go through all the 4-simplices and sum up a number for each 4-simplex. There are two kinds of 4-simplices, and the number depends on which kind of 4-simplex it is. They give an explicit formula for this number.

Here’s my summary of their results:

There’s new evidence that a quantum theory of pure gravity (meaning gravity without matter) makes sense in 4-dimensional spacetime.

To understand why this is exciting, you have to realize that in some quarters, the conventional wisdom says a quantum theory of pure gravity can’t possibly make sense, except as a crude approximation at large distance scales, because this theory is “perturbatively nonrenormalizable”.

Very roughly, this means that as we zoom in and look at the theory at shorter and shorter distance scales, it looks less and less like a “free field theory” where gravitons zip about without interacting. Instead, the interactions get stronger and more complicated!

So, in the jargon of the trade, we don’t get a “Gaussian ultraviolet fixed point”.

Huh?

Well, roughly, an “ultraviolet fixed point” is a quantum field theory that keeps looking the same as you keep viewing it on shorter and shorter distance scales. A “Gaussian” ultraviolet fixed point is one that’s also a free quantum field theory: one where particles don’t interact.

If quantum gravity approached a Gaussian ultraviolet fixed point as we zoomed in, we could calculate what gravitons do at arbitrarily high energies (at least perturbatively, as power series in Newton’s constant - no guarantee that these series converge). Particle physicists would then be happy and say the theory was “perturbatively renormalizable”.

But, it’s not.

The conventional wisdom concludes that to save quantum gravity, we must include matter of precisely the right sort to make it perturbatively renormalizable. This is the quest that led people first to supergravity and ultimately to superstring theory - see “week195” for more of this story.

But, as far back as 1979, the particle physicist Weinberg raised the possibility that pure quantum gravity is “nonperturbatively renormalizable”, or “asymptotically safe”. This means that as we zoom in and look at the theory at shorter and shorter distance scales, it approaches some theory other than that of noninteracting gravitons.

In other words, Weinberg was suggesting that pure quantum gravity approaches a non-obvious ultraviolet fixed point - possibly a “non-Gaussian” one.

The big news is that this seems to be true!

Even cooler, in this theory spacetime seems to act 2-dimensional at very short distance scales.

This idea has been brewing for a long time - I talked about it extensively back in “week139”. But now there’s more solid evidence for it, coming from two quite different approaches.

First, people doing numerical quantum gravity in the “causal dynamical triangulations” approach are seeing this effect in their computer calculations. This is what Renate Loll explained at Loops ‘05. The best place to read the details is here:

19) Jan Ambjørn, J. Jurkiewicz and Renate Loll, Reconstructing the universe, Phys. Rev. D72 (2005) 064014. Also available as hep-th/0505154.

but if you need something less technical, try this:

20) Jan Ambjørn, J. Jurkiewicz and Renate Loll, The universe from scratch, available as hep-th/0509010.

The titles of their papers are a bit grandiose, but their calculations are solid stuff - truly magnificent. I described their basic strategy in my report on the Marseille conference in week206. So, I won’t explain that again. I’ll just mention their big new result: in pure quantum gravity, spacetime has a spectral dimension of 4.02 ± 0.1 on large distance scales, but 1.80 ± 0.25 in the limit of very short distance scales!

Zounds! What does that mean?

The “spectral dimension” of a spacetime is the dimension as measured by watching heat spread out on this spacetime: the short-time behavior of the heat equation probes the spacetime at short distance scales, while its large-time behavior probes large distance scales. Spectral dimensions don’t need to be integers - for fractals they’re typically not. But, Loll and company believe they’re seeing spacetimes that are exactly 2-dimensional in the limit of very small distance scales, exactly 4-dimensional in the limit of very large scales, with a continuous change in dimension in between. The error bars in the above figures come from doing Monte Carlo simulations. They’re just using ordinary computers, not supercomputers. So, with more work one could shrink their error bars and test their result.

My main worry about their work is that it uses a fixed slicing of spactime by timelike slices. So, there’s a danger that their procedure breaks Lorentz-invariance, even in the continuum limit which they are attempting to compute. I would like to find a way around this problem!

Needless to say, this idea that pure quantum gravity has an ultraviolet fixed point is very controversial. Most people working on string theory think it’s false. At present — unlike when I wrote the above — I’m an agnostic.

Posted by: John Baez on July 27, 2008 1:38 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

If there is a UV fixed point, how do you think the generic arguments about black holes, holography, etc. break down? (One version of the argument that these considerations rule out a UV fixed point can be found here.)

Posted by: anon. on July 27, 2008 6:25 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

I don’t know the answer to this question. It seems interesting, but I’m too tired of thinking about quantum gravity to want to ponder it.

Posted by: John Baez on July 28, 2008 9:37 AM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

One more comment:

Have simplicial complexes plus partial ordering swung into your ken at any point?

Yes! For starters, Ambjörn, Jurkiewicz and Loll use a special sort of 4d simplicial complex equipped with a partial ordering, as shown here:

Purely as a matter of mathematical elegance, I’m fond of 4d simplicial complexes where the 4-simplices are partially ordered in a more arbitrary way. These show up very naturally in Oriti and Livine’s work on ‘causal spin foam models’. But, the big problem is getting a theory that reduces to general relativity at large distance scales — and here Ambjörn & Co. seem far ahead of everyone else working on discrete models of spacetime.

I would like to integrate simplicial sets more thoroughly with causality. In a simplicial set, defined algebraically in the usual modern way, each simplex naturally has an ordered set of vertices. Also, each poset gives a simplicial set: its ‘nerve’. But, I don’t see how these ideas help me here.

Posted by: John Baez on July 27, 2008 2:11 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

I wonder if this is related to:

Zeeman, E. C., Causality implies the Lorentz group. J. Mathematical Phys. 5 (1964) 490–493.
Abstract: In a Minkowski space $M$ two events $x$ and $y$ can be ordered if the vector $x-y$ is time-like; in this case $x$ is said to follow $y$ if the time component of $x-y$ is positive. Consider a one-to-one mapping $f$ of $M$ onto itself, such that it preserves the time ordering; it is shown that $f$ coincides with the group generated by the orthochronous Lorentz group, the translations and the multiplication by a scalar. It is interesting to note that this conclusion does not hold if $M$ is two-dimensional.

Posted by: jim stasheff on July 27, 2008 3:24 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

At this point, as most of you know by now, I would generally say something about “diamonds” and “discrete geometry on causal graphs”.

Instead, by now I will assume most everyone here has at least downloaded the paper (if for no other reason than Urs is a coauthor!).

The title was intentionally chosen to indicate some relation to Sorkin’s work on posets. The relation to Loll’s stuff is more tenous, but was certainly an influence in my thinking. The relation to Connes NCG via spectral triples is obvious and together with synthetic geometry firmly puts it within the realm of stuff I would think people here would be interested in.

YET, as far as I can tell, we have been unable to generate ANY interest. Is it me? That wouldn’t really surprise me. When an irritating kid is screaming “Look! Look!” it is understandable that the desire to actually “Look” is diminished.

Anyway, I do apologize. I think this is the last time I will bring it up. I give up.

If you have any criticisms of the paper or doubts about the general applicability, I’d love to hear them so feel free to email me, but I think I’ll stop polluting otherwise interesting discussions.

Best regards

Posted by: Eric on July 27, 2008 5:59 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

Hi Eric,

Speaking from a personal point of view, I should say that that paper looks really interesting but, not knowing a lot about discrete calculus on graphs etc., it’s difficult for me to understand exactly how this paper fits into the bigger picture, how it reveals new things which weren’t known before, etc.

I know this is explained in the introduction (which is nicely written), but I still couldn’t quite grok how it fits in to the bigger picture.

I mean, off-hand: at first sight this would seem like the definitive paper for doing Riemannian geometry (involving the Hodge star operator) on discrete spaces! For instance,

It is easy to treat group-valued functions on the discrete space in the same spirit, which allows us to formulate Yang-Mills field theory on arbitrary background geometries.

I don’t know much about this stuff, but that sounds like an amazing claim. What do the “lattice QFT” people think about this approach? Before reading 80 pages I’d like to have some rough idea of how this fits into the greater scheme of things.

Posted by: Bruce Bartlett on July 27, 2008 8:57 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

Eric wrote:

YET, as far as I can tell, we have been unable to generate ANY interest.

I’m interested! I’ve been interested for a long time. I’ve been wondering why you guys didn’t publish this paper.

Is it me? That wouldn’t really surprise me.

Well, posting grumpy comments like the one above is the absolute worst way to generate interest in ones work. It’s like sitting by the side of the road saying “Come on, buy these eggs! How come nobody EVER buys eggs from me?”

Getting people interested in ideas takes a lot of work, and also a lot of subtlety. You can’t force people to get interested in something, and you certainly can’t scold them into becoming interested. You have to lure them into becoming interested.

Here are some of the usual things people do:

continuing to publish papers that develop the idea and apply it to problems people are already interested in,
giving clear talks about the idea at conferences and workshops — and making the slides available on the web, so people can read them at their leisure,
writing expository accounts of the idea and either publishing these in conference proceedings (the old way, still very important) or on blogs like the $n$ -Category Café (hint hint).

All these take time — and they also take a lot of practice to do well. It’s tricky to simultaneously make ideas seem simple and approachable (so people can start digging into them right away) but also deep and powerful (so people suspect they may be valuable, and become tantalized).

Posted by: John Baez on July 28, 2008 9:23 AM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

I’ve been wondering why you guys didn’t publish this paper.

I always wanted to polish a couple of things before submitting it. Still would. But never got around doing it. It’s a shame. I am feeling bad about it.

The problem is worsened by the fact that by now I understand how what we did back then fits into a bigger picture of noncommutative $\infty$ -Lie theory and AQFT. That makes me want to formulate the whole thing in that context. Which only makes the situation worse.

Posted by: Urs Schreiber on July 28, 2008 10:28 AM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

Urs said:

by now I understand how what we did back then fits into a bigger picture

There’s always a bigger picture. If you wait till you can fit everything into the ultimate big picture, you’ll wait an infinitely long time, then publish an infinitely long paper.

You know this, of course. Just sayin’ …

Posted by: Tim Silverman on July 28, 2008 6:53 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

Urs wrote:

That makes me want to formulate the whole thing in that context.

Don’t.

Posted by: John Baez on July 29, 2008 10:15 AM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

Can you explain for layperson, what 2 dimensional spacetime at short distance mean?

Does it mean the space is quantum analog of 2d films stretched over some 1d carcass in 3d space ? Like space of linear combinations of 2d simplexes ?

Posted by: Serge on July 27, 2008 3:02 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

Serge wrote:

Can you explain for layperson, what 2 dimensional spacetime at short distance mean?

There are different possibilities, and I don’t yet know what’s actually happening in the AJL theory. Does anyone out there know???

But anyway, check out the pictures on page 10 of my talk. This is how I hope things might look in a spin foam model that mimics the AJL theory.

In these pictures, all the dimensions have been divided by 2, to make things easier to draw.

As you note, we really need to take quantum superpositions of these pictures to get the real story!

Posted by: John Baez on July 27, 2008 3:19 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

Won’t that ever lead to particles of the SM?

Posted by: Daniel de França MTd2 on July 27, 2008 6:11 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

For literature searches, it may be useful to note that the four-dimensional simplex is synonymous with the 5-cell and the pentatope.

Weisstein, Eric W. “Pentatope.” From MathWorld–A Wolfram Web Resource.

Posted by: Jonathan Vos Post on July 28, 2008 12:32 AM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

I’d never seen the word ‘pentatope’ until I read some Wikipedia articles on regular polytopes. I wonder when the last math paper was written using this term. It has a charming 19th-century ring to it, like ‘tesseract’. Does anyone still use it?

As for ‘5-cell’, most mathematicians use this to mean any space homeomorphic to a 5-dimensional closed ball. They especially do this in the theory of CW complexes. I’d never heard ‘5-cell’ used to mean ‘4-simplex’ until just now.

Posted by: John Baez on July 28, 2008 10:16 AM | Permalink | Reply to this

Pentatope numbers; Re: Causality in Discrete Models of Spacetime

The next step up from Triangular Numbers, and Tetrahedral Numbers, is Pentatope Numbera.

The first few pentatope numbers are 1, 5, 15, 35, 70, 126, … (Sloane’s A000332).

as in:
A000332 Binomial coefficients binomial(n,4).

Hyun Kwang Kim, On regular polytope numbers, Proc. Amer. Math. Soc. 131 (2003), 65-75.

Weisstein, Eric W. Pentatope Number.” From MathWorld–A Wolfram Web Resource.

I don’t diagree about the sound from anther centuury, as with Tesseract, but I do like Pentatope numbers.

A100009 Iterated pentatope numbers, starting with Ptop(2) = 5. The pentatope number of the pentatope number of the pentatope number … of 2.

Posted by: Jonathan Vos Post on July 28, 2008 3:19 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

Jonathan wrote:

The first few pentatope numbers are 1, 5, 15, 35, 70, 126, … (Sloane’s A000332).

‘Pentatope numbers’ sounds cute, but most mathematicians call ‘em binomial coefficients: $\binom{n}{4}$ . For the obvious generalization from the 4-simplex to the $k$ -simplex, use $\binom{n}{k}$ .

This doesn’t have too much to do with causality in discrete spacetimes…

Posted by: John Baez on July 28, 2008 4:17 PM | Permalink | Reply to this

On Regular polytope numbers, Re: Causality in Discrete Models of Spacetime

That would all be true. Except that the fine paper by H. K. Kim, “On Regular polytope numbers”, does not restrict itself to the simplex numbers.

Kim cleverly points out that Lagrange’s Four-Squares Theorem can be generalized in two orthogonal directions in the ideocosm.

One is to replace “square” by “regular n-gon”, thus getting the Guass result that every positive integer can be written as the sum of three triangular numbers, four squares, five pentagonal nukbers, six hexagonal numbers, and so forth.

The other is to replace “square” by cube, biquadrate, 5th powers, and the like. This leads to Waring’s problem(s).

Now, moving along both of these axes in the space of all possible theories, we need to consider replacing the cubes in Waring’s Problem, by the figurate number analogues of regular tetrahedra, octahedra, dodecahedra, and icosahedra.

Now, on going up to 4-dimensional Euclidean space, we have figurate number analogues not only of tetrahedral numbers (the aforementioned pentatope numbers) but also hyperoctahedron numbers, and the analogues constructed from the 24-cell, the 120-cell, and the 600-cell polytopes.

These numbers are all in OEIS also, as for instance in:

A099197 Figurate numbers based on the 10-dimensional regular convex polytope called the 10-dimensional cross-polytope, or 10-dimensional hyperoctahedron, which is represented by the Schlaefli symbol {3, 3, 3, 3, 3, 3, 3, 3, 4}. It is the dual of the 10-dimensional hypercube.

The first few values are: 0, 1, 20, 201, 1360, 7001, 29364, 104881, 329024, 927441, 2390004, 5707449, 12767184, 26986089, 54284244, 104535009, 193664256, 346615329, 601446996, 1014889769, 1669752016, …

Of course, for dimension D above 4 we need only construct the analogues of the tetrahedral numbers, D-th powers (hypercubes), and their duals (whether one calls the hyperoctahedron numbers or cross-polytope numbers or whatever).

I do intend to get back to the main thread by posting some results that I have not seen elsewhere on (not necessarily convex) poly-pentatopes in Euclidean space, analogues of polyiamonds in 2-D and Polytetrahedra in 3-D. These are easier for nonphysicists to grasp than the analogues in hyperbolic spaces, such as Minkowski space, where this thread began.

Posted by: Jonathan Vos Post on July 28, 2008 5:31 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

Loll used the term “fractal-like” which produced some discussion as to what she meant. There’s a fractal-like visual pattern created by the pentatope numbers inside Pascal’s Triangle.

Reconstructing the Universe Authors:
J. Ambjorn, J. Jurkiewicz, R. Loll
“A closer look at the quantum geometry reveals a number of highly nonclassical aspects, including a dynamical reduction of spacetime to two dimensions on short scales and a fractal structure of slices of constant time. …

Because our universes have a well-defined global notion of (proper) time ? , it is relatively straightforward to perform measurements within a slice of constant?. We first restrict ourselves to slices S of integer-? . Such slices consist entirely of spatial tetrahedra (whose
edges are all spacelike). The slices are of the form of spatial interfaces of topology S3 between adjacent sandwiches made out of four-simplices. As we will see, the Hausdorff dimension of the slices turns out to be three, as one would have naively expected in a
four-dimensional universe.
However, the slice does not behave three-dimensionally under diffusion, and we will see that its structure is fractal in a precise sense which will be described below.”

http://milan.milanovic.org/math/english/pentatope/pentatope.html
Pentatope Numbers (4-tetrahedron numbers) can be found in the fifth column of Pascal`s triangle, which are of course the sum of the tetrahedral numbers.

http://ptri1.tripod.com/
When all the odd numbers (numbers not divisible by 2) in Pascal’s Triangle are filled in (black) and the rest (the evens) are left blank (white), the recursive Sierpinski Triangle fractal is revealed (see figure at near right), showing yet another pattern in Pascal’s Triangle.

Posted by: Stephen Harris on July 29, 2008 2:20 AM | Permalink | Reply to this

Re: Dimensions

I’m having some difficulty understanding the claims about dimensionality in this model. I have a rough idea how dimensionality is defined – I guess you let “test particles” random-walk through the graph, and see how their average distance scales with the number of steps? What I’m having trouble with is understanding how you can start with a fixed 3d manifold, stick a sequence of triangulations of it together with a fixed time-ordering, and end up with anything but a 4d structure. That is, I’m failing to understand why the 4d-at-large-scale result is impressive, and how the 2d-at-small-scale result even makes sense.

To help think about this, let’s drop down a dimension: what kinds of space can we get by sticking together a sequence of triangulated 2d sheets? The overall dimension must depend on the way the slices are stuck together, of course… If we think of the sheets stuck together in a very “orderly” fashion – like a stack of chess boards with connecting vertical edges between corresponding vertices – then we end up with an obviously 3d structure. But what if we do something different? It can’t be a matter of adding more or fewer connecting edges, because the valence of the vertices is fixed (right?). So all we’re left with is shuffling the connecting edges – changing which vertices on sheet n connect to which on sheet n+1. Is there some intuitive way to see that choosing the connections appropriately leads to a graph that looks higher- or lower-dimensional?

Posted by: Stuart on July 28, 2008 10:23 AM | Permalink | Reply to this

Re: Dimensions

$MathML-enabled post (click for more details).$

Stuart wrote:

I have a rough idea how dimensionality is defined — I guess you let “test particles” random-walk through the graph, and see how their average distance scales with the number of steps?

Exactly. This gives the ‘spectral dimension’.

If a particle carries out Brownian motion on Euclidean $n$ -dimensional space, its probability of being at the point $\vec{x}$ smears out with the passage of time in a way that depends on $n$ :

$p(t,\vec{x}) = \frac{1}{{(4 \pi k t)}^{n/2}} e^{-x^2 /4 k t}$

where $k$ is a constant that measures the rate of the particle’s diffusion.

Given any sort of geometrical object, we can try to use this idea to compute a ‘spectral dimension’ for it. But we may get different values for the ‘large-scale’ dimension (computed using large $t$ ) and the ‘small-scale’ dimension (computed using $t$ near zero). For example, we can take a bunch of tiny 1-dimensional threads and weave them into a big 3-dimensional pillow.

What I’m having trouble with is understanding how you can start with a fixed 3d manifold, stick a sequence of triangulations of it together with a fixed time-ordering, and end up with anything but a 4d structure. That is, I’m failing to understand why the 4d-at-large-scale result is impressive, and how the 2d-at-small-scale result even makes sense.

I don’t understand this either. I’ve asked, but I’ve never gotten Loll or anyone else to paint me a vivid mental picture of what’s going on with their results. I’m not sure anyone knows the picture! This makes me very unhappy.

If one ignores the time-ordering and simply sticks 4-simplexes together, it’s easy to get a lot of 4-simplexes all touching each other. This gives a large-scale spectral dimension of zero: a blob viewed from afar looks like a point. In some quantum gravity simulations, configurations of this sort dominate: this is called the crumpled phase.

It’s also possible to stick 4-simplexes together in a complicated branching tree structure. This is called the branched polymer phase. I forget the large-scale spectral dimension here.

In my talk, I made a feeble stab at understanding how to get a small-scale spectral dimension of 2 in a spin foam model. The idea is that a spin foam looks like a bunch of soap suds.

Ordinary soap suds has a large-scale spectral dimension of 3; in a realistic spin foam model of quantum gravity we probably want a large-scale spectral dimension of 4. But soap suds made from idealized infinitely thin bubbles has a small-scale spectral dimension of 2, since when you zoom in very close to a point on a soap bubble, you generically see something 2-dimensional.

However, this idea of mine was very primitive. It would need a lot of development before it amounted to much.

And, I don’t really see how it’s connected to the work of Ambjörn, Jurkiewicz and Loll!

Posted by: John Baez on July 29, 2008 10:55 AM | Permalink | Reply to this

Re: Dimensions

I can (roughly) imagine how you might get something of lower dimension by sticking together 4-simplexes in various ways – crunching them together to get a 0-dimensional blob, or chaining them together to make a 1-dimensional strand (or a tree of these), or a 2-dimensional sheet, etc. And if you don’t put any further constraints on how the 4-simplexes get stuck together, I can believe that the most common structures to emerge might not look much like familiar spacetime.

There are a couple of fairly obvious (and related) ways we might try to force the end result to be more like spacetime.

Firstly, we could say that each 4-simplex has some (partial-)ordering on its vertices, which needs to be respected somehow when 4-simplexes are glued together. We could hope that this would force a certain amount of “orientation” to be preserved at the larger scale, which could perhaps correspond to a time-direction. But its not obvious why this would force the emergent spacetime to be 4-dimensional.

The other option, which seems to be what AJL are doing, is just to put in the 4-dimensionality by hand, by defining spacetime to be a sequence of triangulated 3-manifolds. In that case, it’s harder to see why recovering 4-dimensionality at large scales should be surprising. The 3-manifolds surely can’t forget their 3-dimensionality in the process of triangulation (right?), so all that remains is that the sticking-together process doesn’t add links in such an odd way as to mess up the dimension… OK, so maybe it is somewhat surprising that this works out OK. :)

As regards the small-scale 2-dimensionality: can we look at the 4-simplexes that make up some particular 2d structure and determine whether they all came from the same triangulated 3-manifold, or whether they instead came from a sequence of successive 3-manifolds (i.e. whether this 2d structure is a spacelike sheet, or the world-sheet of some 1d strand)? Might it turn out that this 2-dimensionality result is telling us that spacetime is, at small scales, made up of 1d strands tracing out world-sheets as they move forward in time? (Why does that sound familiar? :) )

Posted by: Stuart on July 29, 2008 7:21 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

I only have an extremely patchy understanding of the various discrete approaches to quantum gravity, but I’m aware that there are quite a few different models that all share at least a family resemblance. Is there anywhere I might find a good summary of the current state of the field, that sets out the various approaches – LQG, CDT, causal sets, spin foams, et al. – in a manner that’s approachable to beginners, and makes clear the common features and the differences between them?

Also, is there a lot of work currently being done on unifying these different ideas? I listened to the audio of Carlo Rovelli’s recent talk at QGQG at Nottingham, in which he seemed to say that LQG is basically just the Barrett-Crane spin-foam model “done right”. Did I misunderstand that? If true, that seems like a pretty important unification! Is there other work ongoing to tie together the different discrete quantum gravity models?

Posted by: Stuart on July 28, 2008 11:04 AM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

various discrete approaches to quantum gravity, […] LQG

I have problems with the statement that LQG (in the former sense of the word: probe spaces of generalized gauge connections by evaluating these on Wislon networks aka spin networks) is a discretization approach to quantum gravity. Spin networks are a choice of basis, not a physical entity. If the configuration space of connections one starts with is one on a non-discrete manifold – as it is in LQG – then the theory is not a discrete one.

Whether or not the final quantization has volume observable operators with discrete spectrum is different issue. If something like this were to hold true, we’d have “emergent” discreteness obtained from a continuum theory, not the other way round.

But if this is true is unknown. The argument has always been applied to pure spin network states. But these don’t live in the physical Hilbert space. Last I checked, nobody knew what the physical Hilbert space is, nor even how precisely it should be defined.

All this is different if by “LQG” one means something else, such as certain state sum models. It seems that different poeple nowadays can mean very different things when they say “LQG”.

Posted by: Urs Schreiber on July 28, 2008 1:28 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

i keep thinking that the tools of domain theory ought to have some applicability, here. In particular Martin and Panangaden have shown that they can recover a highly faithful picture of geometry from causality using domain theoretic techniques.

Posted by: Meredith Gregory on August 6, 2008 7:13 AM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

Have any of you read these papers by Manfred Requardt,

The Continuum Limit of Discrete Geometries

and

About the Minimal Resolution of Space-Time Grains in Experimental Quantum ?

If so, I’d very much appreciate your comments on them. I have an entry here, in case you find it more appropriate for commenting.

Thanks.

Posted by: Christine Dantas on August 15, 2008 1:47 PM | Permalink | Reply to this

Re: Causality in Discrete Models of Spacetime

$MathML-enabled post (click for more details).$

I haven’t looked at these papers in detail, but I’m happy to see that in the second paper, at least, Requardt agrees with Jay Olson and me in doubting a certain claim made by Ng and van Dam. These authors claimed there is a fundamental uncertainty in our measurement of distances which grows as the distance being measured increases. We argued otherwise.

Requardt disagrees with some aspects of our thought experiment — he thinks we were overly optimistic in how accurately distances can be measured with a linear rod. But, I’m happy that he seems to our agree with our final conclusion, namely that there should be a fundamental uncertainty in our measurement of distances that’s on the order of the Planck length, regardless of the distance being measured.

Posted by: John Baez on August 17, 2008 1:20 AM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

July 27, 2008