Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

May 18, 2007

Penrose on Angular Momentum: An Approach to Combinatorial Space-Time

Posted by John Baez

Georg Beyerle has created an electronic version of a classic paper on spin networks that was previously available only in an out-of-print book:

Roger Penrose has given me permission to put it on my website. Take a copy! If you spot typos, please let me know.

Here’s what a piece of a spin network looks like:

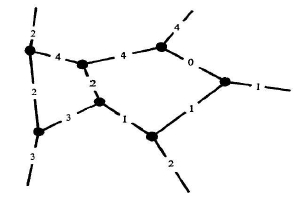
Can we build space, or spacetime, out of something as simple as this? That’s the question Penrose tackles in his paper.

Posted at May 18, 2007 4:12 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1277



4 Comments & 0 Trackbacks

Re: Penrose on Angular Momentum: An Approach to Combinatorial Space-Time

This is one of my all time favorite papers. Thanks for making it available electronically!

Posted by: Eric on May 18, 2007 5:53 AM | Permalink | Reply to this

Re: Penrose on Angular Momentum: An Approach to Combinatorial Space-Time

That reminds me: still have to work out the general concept of tracing a parallel nn-transport to a holonomy, such that Wilson networks/spin networks and Wilson surfaces/spin foams come out by turning the crank.

Should involve something about general traces.

What I don’t quite see yet: is the fact that, for n=1n=1, we may have different representations on edges whith intertwiners on the vertices a phenomenon that should ultimately be attributed to the fact that 1-dimensional cobordisms don’t have branchings unless we do something about it (i.e. that the point-particle limit of the pair-of-pants no longer a manifold) – or do we even want to work with nn-intertwiners of nn-representations for Wilson nn-networks?

Another aspect of this question might be: do we need Wilson networks which involve different reps to distinguish points in our configuration space of connections?

That will depend, I guess, on how precisely this space is defined.

Posted by: urs on May 18, 2007 11:23 AM | Permalink | Reply to this

Re: Penrose on Angular Momentum: An Approach to Combinatorial Space-Time

To detect the difference between two smooth SU(2)\SU(2) connections mod gauge transformations, it suffices to use Wilson loops labelled by the spin-1/2 representation. This old theorem is the basic idea behind loop quantum gravity.

The same is true for SU(n)\SU(n) connections if we label our Wilson loops by the defining nn-dimensional representation of SU(n)\SU(n).

However, these Wilson loops satisfy a bunch of linear relations, called ‘Mandelstam identities’. It’s nice to have a linearly independent set of gauge-invariant functions on the space of connections.

For this, it’s more convenient to work with Wilson graphs with edges labelled by arbitrary irreps of the gauge group, and vertices labelled by arbitrary intertwining operators. These are now called ‘spin networks’ — they’re a generalization of Penrose’s original idea.

Spin networks give a basis for a certain nice space of functions on the space of connections mod gauge transformations:

Moreover, spin networks work for any compact connected Lie group, not just SU(n)\SU(n).

Posted by: John Baez on May 18, 2007 5:51 PM | Permalink | Reply to this

Re: Penrose on Angular Momentum: An Approach to Combinatorial Space-Time

John Baez, Spin network states in gauge theory.

Thanks! I am printing it out, will read it on the train that takes me into the week end (am feeling so stupid not knowing in suficient detail all this old work of yours…).

More later.

Posted by: urs on May 18, 2007 6:14 PM | Permalink | Reply to this

Post a New Comment