Lie Theory Through Examples 2
Posted by John Baez
In this week’s seminar on Lie Theory Through Examples, we’ll move on up to the lattice.
You’ve seen this lattice before: when you stack spheres in a triangular pyramid, their centers lie at points that form a lattice of this sort:

But to derive this lattice starting with the Lie group , we’ll need to talk a bit about the Killing form. That’s what allows us to measure angles and distances in the Lie algebra.
- Lecture 2 (Oct. 6) - The Killing form and the lattice.
A different view makes it clear why the A3 lattice is also called a "cubic close packing":
You can also think of the A3 lattice as built from octahedra and tetrahedra. This figure is from Buckminster Fuller’s patent for the "octet truss", now widely used in architecture:
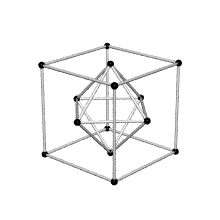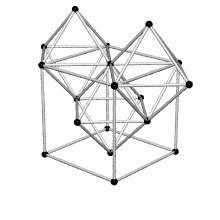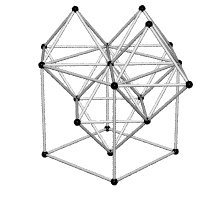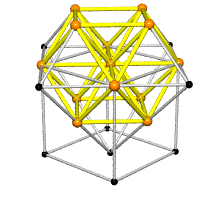
In the lattice, each point has 12 nearest neighbors.
These form the vertices of a cuboctahedron:







Re: Lie Theory Through Examples 2
Wait, was the lecture really on Monday?