Re: Modular Forms
Tim writes:
My understanding (if you can call it that) is that the inclusion of in the modular group gives rise to a covering of by , and lifting the fundamental domain of to the covering gives a tiling of the surface by regular -gons, 3 meeting at each vertex, each subdivided into triangles corresponding to the fundamental domain of the modular group.
I’m way behind you, so let’s see if you (or anyone!) can help me unnderstand this.
For our TV viewers out there, let’s first recall that is the group of matrices with integer entries having determinant 1, better known as . Or, maybe it’s this group modulo , better known as . Which group we use doesn’t matter a lot for what we’re doing now, as long as we’re consistent about it. So, let me not mod out by , at least in this comment.
Then is the subgroup of consisting of those matrices whose entries are equal, mod , to those of the identity matrix.
This is a normal subgroup, and I guess
at least when is prime. Is this right? Does this make sense when is not prime?
and thus acts on the upper halfplane , and we’re mainly interested in , which is a covering space of .
I know and love , and I want to know and love .
So, I’ll do what you say and think of as a covering space of . Or, equivalently, I’ll think about a fundamental domain for the action of on as made of a bunch of fundamental domains for the action of on .
Here are a bunch of fundamental domains for the action of on :
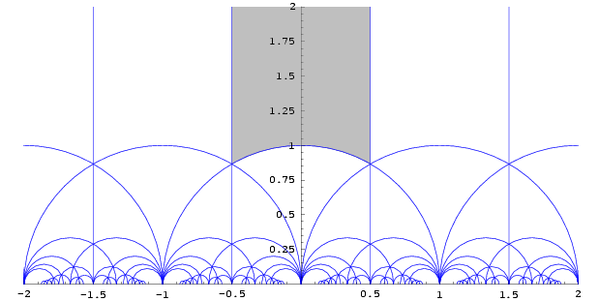
The gray one is everybody’s favorite. It’s a ‘triangle’ with two corners having 60-degree angles and one corner infinitely far up the page with a 0-degree angle — that very pointy corner is what gives the ‘cusp’.
So, how do I create a fundamental domain for by taking a bunch of fundamental domains for ?
For starters, how many do I need? It must be the cardinality of , no? That should be the cardinality of , no? At least when that makes sense?
But wait — now I think the right answer is the cardinality of . We really need to think about groups that act faithfully on , so we need to mod out by everywhere.
Which is it?
Let’s see: what’s the cardinality of ? First, what’s the cardinality of ? There are choices for the first row of the matrix, and choices for the second row. So, . Of these matrices, of them have determinant 1. So, there are
matrices in .
Let me check — I usually make mistakes in calculations like this. For , this formula gives 6, which fits the idea that .
For this formula gives , which matches the idea that , half as big, is .
This also fits your formula which says that for prime , there’s a tiling of by
-gons, each of which consists of triangles, for a total of
triangles. Sort of like this for :

I believe there are triangles in this picture: 14 triangles per heptagon, 24 heptagons in all. If I’m wrong, I must be making a serious mistake somewhere.
Hmm, so the number of triangles is the cardinality of , not ? At least when is prime?
Anyway, I eventually wish to get to more interesting questions, but for now let me quit while I’m ahead (or behind).
Re: Modular Forms
I want to discuss in more detail the spaces , and , that is, the quotients of the upper half plane by , and respectively (with cusps filled in). I also want to talk about the actions of the Hecke operators and on modular forms—or at least the corresponding actions on modular curves. Alas, I don’t think I’m going to get there in this post, but I can at least make a start.
But before I talk about all that, I want to talk about Farey sequences!
I was introduced to Farey sequences by a maths teacher at school, when I was about 13 or so, one afternoon when I’d done all my work and was feeling bored. They’re a simple and cute idea, and I found them kind of fascinating, but, not being much of a number theory person, I never looked into them all that deeply. But one stumbles across these things in the oddest places.
What is a Farey sequence? It’s very simple. Take all the reduced fractions from 0 to 1 (inclusive) with denominators no larger than some maximum . Now arrange them in order of increasing value. And that’s a Farey sequence. Thus Farey sequences include
and so on. Here’s the ninth Farey sequence:
There are some curious facts about Farey sequences. Here’s one: if and appear adjacent to one another in some Farey sequence, then .
Here’s another: if and appear adjacent to one another in some Farey sequence, then the next fraction which gets inserted between them, as you work your way through the successive Farey sequences, is the fraction . This funny combination is called the mediant of and , since it always lies between them. By repeatedly taking mediants, we build up all Farey sequences, and hence get each rational number from to exactly once.
We can indicate the way that the mediant derives from two parent fractions by drawing lines from the parents to their mediant:
Farey Sequence as tree
0/1
1/1
1/2
1/3
2/3
1/4
3/4
1/5
4/5
2/5
3/5
A Farey sequence in tree form
Additionally, one of the parents must always derive from the other—it must have been inserted as a mediant itself at some earlier time. So if a fraction is connected to its parents by a pair of lines, the parents must also be connected to each other. So these lines actually make up a bunch of triangles, except at the top of the picture where everything starts. Taking the three numbers at the vertices of a triangle, any one of them can be derived from the other two either as their mediant, , or as what we might call their ‘mediant difference’, . In fact every pair of numbers joined by a line belongs to two triangles (one on either side of the line joining them), and one of the triangles will contain their mediant as its third point, while the other will contain their mediant difference instead!
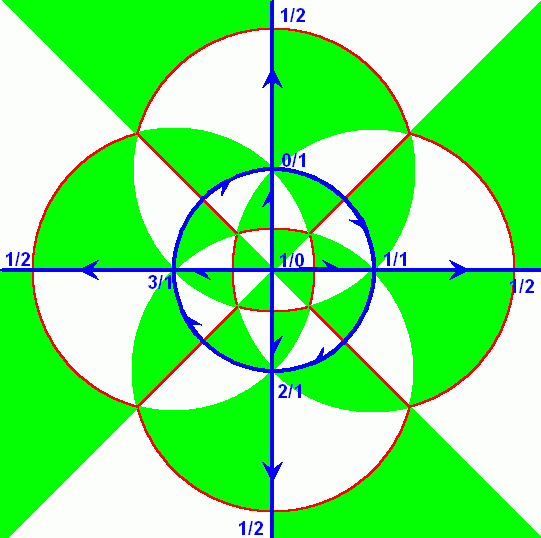
So, can the Farey tree be extended to include fractions outside the interval ? That’s something we might be wondering, and the answer is Yes! In fact, this would have happened already if we hadn’t foolishly forgotten something: we’ve included fractions with denominators of , , , etc, but we’ve forgotten to include fractions with denominator ! How could we have been so careless? Let us remedy this oversight at once!
Including the fraction right at the top of the tree, it turns out that we can actually derive from this together with , as their mediant, and then we can get from and , and so forth, and by building up mediants, we can get all non-negative rational numbers that way. The whole tree is called the Stern-Brocot tree.
Stern-Brocot tree
1/0
0/1
1/1
2/1
1/2
3/2
1/3
2/3
4/3
5/3
1/4
3/4
5/4
7/4
1/5
4/5
2/5
3/5
6/5
9/5
7/5
8/5
A piece of Stern-Brocot Tree
Once we’ve made these extensions, and added an edge connecting and , we see that every fraction in the tree, including the ones right at the top, belongs to a triangle—in fact, it belongs to an infinite number of triangles! We can just keep forming new mediants from it with its new neighbours forever.
However, an infinite number of triangles hanging off every vertex is rather unmanageable. Is there some way we can get a toy version, with only a finite number of triangles instead? For instance, suppose we mod out the fractions by some natural number ? That is, we mod out both numerator and denominator by , taking care not to forget that ? Then many different -fractions will map to the same -fraction, and if we identify the corresponding points, and also, of course, identify the corresponding edges connecting corresponding points, then we will get something finite.
For instance, suppose we take the above tree mod (reducing the fractions where necessary to their lowest form, and bearing in mind that , so ). We get this:
Stern-Brocot Mod 3
1/0
0/1
1/1
2/1
2/1
0/1
1/0
1/0
1/0
1/0
1/1
0/1
2/1
1/1
2/1
2/1
1/1
0/1
0/1
0/1
2/1
1/1
A piece of Stern-Brocot Tree Mod 3
Or reducing mod (and bearing in mind that and , we get this:
Stern-Brocot Mod 4
1/0
0/1
1/1
2/1
1/2
1/2
3/1
2/1
0/1
2/1
1/0
1/0
1/0
1/0
1/1
0/1
2/1
3/1
2/1
3/1
3/1
0/1
A piece of Stern-Brocot Tree Mod 4
The rule about mediants and mediant differences still applies, but sometimes, with all the swapping of signs, we’ve switched around which fraction relates to which how!
Anyway, with these trees in hand, all we need to do is identify the vertices and edges correctly, and we’ll get something interesting and finite. In fact, while we’re about it, why not fill in those triangles? Then we’ll get a compact surface! It will be triangulated, and in fact each vertex will be the apex of just triangles (this is completely obvious in the case of the vertex , but it applies to all vertices). Or, dually, every vertex will stand at the centre of an -gon, while each of the triangular faces gives rise, dually, to a vertex at which -gons meet.
Wait a minute …
That sounds familiar …
Could it be … ?
Yes it is! The compact surface we have just constructed is none other than , the quotient of by . Quel surprise! The fractions mod correspond to the cusps, and we can make the dual tiling completely regular if we pick the right constant-curvature metric (which will need positive curvature for , negative curvature for , and will have to be flat for ).
In fact, this also works for the full Stern-Brocot tree, without any modding out, with fractions over all integers. We can see this either arithmetically or geometrically.
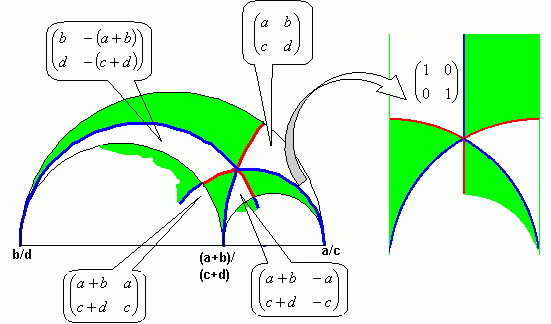
Arithmetically, replace the fraction by the element in . Of course, acts on this by ordinary matrix multiplication; indeed, acts on it too, more nicely, since switching the signs of both numerator and denominator doesn’t affect the value of the fraction.
In particular, if we pick an element of such as , then those two starting fractions at the top of the tree, and , will get sent, under the action of that group element, to a pair of fractions and such that . (That minus sign is a result of listing the fractions the ‘wrong’ way around). This same relation holds true of any two adjacent elements in a Farey sequence, and since some member of is available to send and to any adjacent pair, we get all Farey sequences in this way—over all integers, not just in the interval .
Now, and are joined to each other by an edge, and, being adjacent elements of a Farey sequence, so will their images be. In addition, each of and is also joined by an edge to , their mediant. But the mediant of fractions corresponds simply to the sum in (considered as a -module). And obviously the sum relation is preserved by . So if gets sent to and gets sent to , then gets sent to the mediant of and , meaning that the other two sides of that top triangle -- are also preserved—sent to sides of a triangle in the image.
So triangles are sent to triangles. Moreover, since the relation of being the mediant (or sum) of the other two vertices—as opposed to their mediant difference (or difference)—uniquely picks out one vertex of a given triangle, and since the sign of the determinant—or, more simply, which of the parent vertices is larger—uniquely picks an orientation of the triangle, each triangle is sent to another triangle in only one way. So acts freely on the set of triangles, and of course preserves their relations.
Geometrically, as we can see from Don Hatch’s nice Hyperbolic Tesselations web page, the tilings of the hyperbolic plane by regular -gons, meeting at each vertex, have a limiting case with a tiling by what one might call regular -gons, or regular -gons, with an infinite number of sides! They appear in the website as {infinity, 3}. Dually, we get a tiling by triangles, an infinite number of which meet at the ‘centre’ of each -gon. These triangles correspond precisely to the triangles in the Stern-Brocot tree. Rather confusingly, however, in the Poincaré disk model, the ‘centre’ of a -gon appears at the edge of the disk—that’s the sort of thing that happens when you have an infinite number of sides and are trying to show them all in a bounded region.
If we compare the Poincaré disk model of the hyperbolic plane with the ‘upper half-plane’ model, we see that the real line of the latter goes to the boundary circle of the former. The -gons, drawn in the Poincaré disk, are all tangent to the boundary circle, each with its own distinct point of tangency, and these points correspond precisely to the rational numbers (together with ). In turn, these rational numbers are the ones in the Stern-Brocot tree, i.e. at the vertices of the triangles, which can also be seen as tiling the hyperbolic plane, dually to the -gons. In this way, we also get to label each -gon by a unique rational number, and this is inherited when we go over to the version mod —fractions also being reduced mod .
Given all this, one way to try and understand the way that geometry and arithmetic interact in is by working our way down the Stern-Brocot tree mod , which will correspond to working our way outward from one of the -gons in . What we’re going to see is a series of concentric circles of fractions with successively incrementing denominators.
But that, I think, is something for another post.







Re: Modular Forms
I’m not fully sure about this stuff but I think I understand it well enough at level 2. The moduli space looks like a Riemann sphere with three holes poked in it. (I think they’re actually called cusps, but I think of them as holes poked in the surface)
There are two level-one modular forms, which I know how to get in two ways:
The fourth powers of the Jacobi theta functions at z=0–there are three values but the fourth powers are not linearly independent, and the Jacobi identity brings it to two, or
The Weierstrass p functions at 1/2, , and (when you take 1 and to be the periods rather than the half-periods–I don’t know what the convention is), which always add up to 0. Also note that those three points are also precisely the points(modulo periods) where the derivative is zero.
Either basis can be described in terms of the other(and I think the Wikipedia pages describe how exactly to do that).
Higher-order(I can’t remember the exact term) modular forms are expressed in terms of these, and you can tell when it’s level-1 when you get one symmetric in the three generators. (That’s why you use three instead of two, despite only two being linearly independent)
There’s one fundamental modular function, the elliptic lambda, which takes values 0, 1, and infinity on the cusps.
I’m not fully sure about levels 3 and higher(most of this stuff I figured out myself/with the help of Wikipedia/MathWorld a few years ago, and I’m only seventeen so I probably shouldn’t know this at all, and take it with a grain of salt) but I do know that there’s a really nice link to Platonic solids on levels 3, 4, and 5. Can’t really tell you much more than what the moduli spaces look like, though.
On levels 3-5 the moduli space is a Riemann sphere with cusps.
On level 3, there are 4 cusps, the vertices of a tetrahedron.
On level 4, there are 6 cusps, the vertices of an octahedron.
On level 5, there are 12 cusps, the vertices of an icosahedron.
On level 6, you have a torus. I don’t remember how many cusps it has but if you fill in all the holes it’s isomorphic to the plane modulo the Eisenstein integers(or, in elliptic curve form, )
On level 7 you have the Klein quartic. There are 24 cusps, related to tiling the quartic with heptagons and/or triangles.
And after that my knowledge is pretty much exhausted.