This Week's Finds in Mathematical Physics (Week 274)

March 12, 2009

This Week’s Finds in Mathematical Physics (Week 274)

Posted by John Baez

$MathML-enabled post (click for more details).$

In week274 of This Week’s Finds, see a gorgeous view of a Martian crater. Learn about infinite-dimensional 2-vector spaces, and representations of ‘2-groups’ on these. Get a hint of how representations of the Poincaré 2-group arise from pictures like this:

And learn about Mackey’s classic work on unitary group representations!

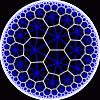
$MathML-enabled post (click for more details).$

The picture above, drawn by Don Hatch, is one of many beautiful tesselations of the hyperbolic plane. It’s called {7,3} since it’s built from regular heptagons, 3 meeting at each corner. If we mod out by a certain symmetry group, the heptagons get identified as shown here…

… and we’re left with a tiling of a 3-holed torus by 24 regular heptagons — or dually, by 56 equilateral triangles, like this:

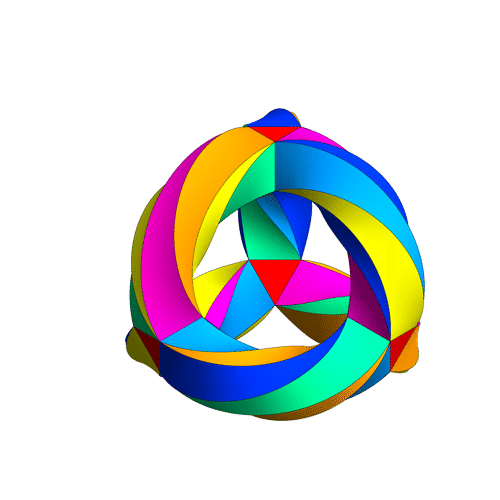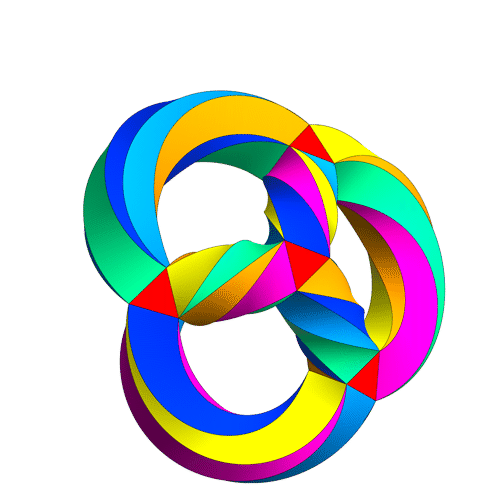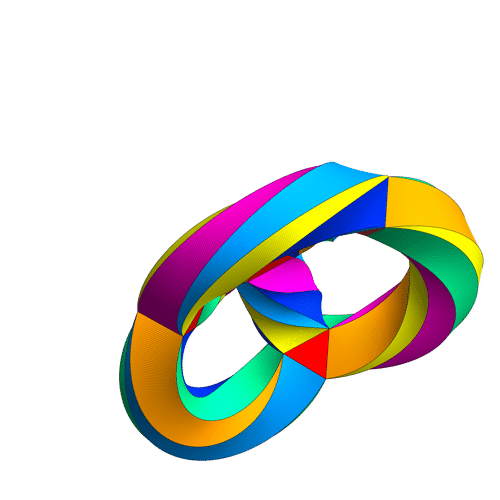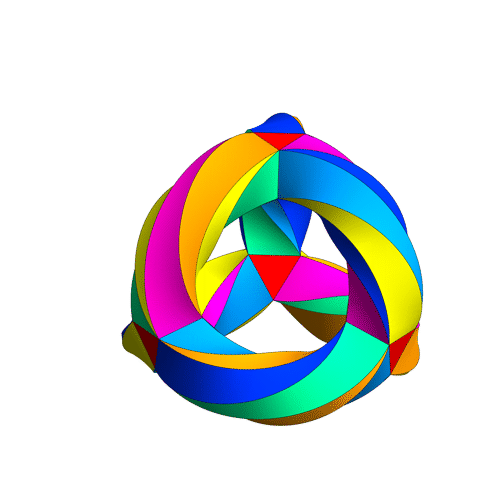
This puts a maximally symmetrical conformal structure on the 3-holed torus. The result is called Klein’s quartic curve.

There are lots of nice relations between such quotients of hyperbolic space by discrete symmetry groups and the theory of modular forms.

So: can anyone develop deeper links between representations of the Poincaré 2-group and modular forms?

The relation between measurable fields of Hilbert spaces and coherent sheaves of vector spaces may hold a clue…

Posted at March 12, 2009 8:51 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1931

13 Comments & 0 Trackbacks

Re: This Week’s Finds in Mathematical Physics (Week 274)

Random walks on groups play an important role in the theory of rapidly mixing Markov chains. Do you think there any chance of defining a (useful) version this concept for 2-groups ?

Posted by: G. on March 13, 2009 2:07 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

$MathML-enabled post (click for more details).$

In our work on higher gauge theory, Urs Schreiber and I showed that just as the holonomy of a connection along a path takes values in a group, the holonomy of a ‘2-connection’ along a ‘2-path’ takes values in a 2-group. A 2-path is a path of paths, i.e. a 1-parameter family of paths.

So, if random paths on groups are good, random surfaces in 2-groups may be good as well. Just as the former can be thought of as a particle randomly roaming around a group, the latter can be thought of as a string randomly wiggling around in a 2-group — I guess.

(I’m not sure I can parse the phrase ‘a string randomly wiggling around in a 2-group’. But the Euclidean-signature version of the Wess–Zumino–Witten model can be thought of as a string randomly wiggling around in a group, and Urs has shown that a 2-group naturally enters this story.)

There’s aready an extensive theory of random surfaces, generalizing the theory of random walks. I don’t know much about it.

Posted by: John Baez on March 13, 2009 5:55 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

In his book on quantum gravity, Rovelli motivates the use of the concept of a holonomy of connection along a path right at the beginning. I wonder whether the isotropy of space is an implicit assumption on taking that path an undirected path (without a directional structure, like a local partial order on it). I wonder whether at the Plank scale, the isotropy of space is broken, and perhaps, if my reasoning above is correct, one would have to consider directed paths, or some other proper modification. And now I wonder whether 2-paths (or higher) would make an alternative possible model for the holonomy in an anisotropic space at a quantum gravity regime; the degree of the anisotropy being taken in consideration by the use of higher and higher paths. Thanks for any clarification.

Posted by: Christine on March 13, 2009 6:32 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

$MathML-enabled post (click for more details).$

Christine writes:

I wonder whether the isotropy of space is an implicit assumption on taking that path an undirected path (without a directional structure, like a local partial order on it).

I don’t see what the isotropy of spacetime has to do with it: in general relativity, there are lots of lumpy spacetimes that aren’t at all isotropic, but nonetheless parallel transport is defined using the holonomy of a connection in the usual way.

To define the holonomy of a path we need to pick a direction for that path; the reverse path has the inverse holonomy. It’s fun to think about dropping that last assumption, though.

Posted by: John Baez on March 15, 2009 5:11 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

John Baez wrote:
I don’t see what the isotropy of spacetime has to do with it: in general relativity, there are lots of lumpy spacetimes that aren’t at all isotropic, but nonetheless parallel transport is defined using the holonomy of a connection in the usual way.

Yes, such lumps may be anisotropic but is it not correct to say that their description can be made mechanically equivalent in the sense that you can always find a local frame of reference in which their description is simpler (isotropic)? This is what I was wondering about: I thought that somehow there was some implicit assumption about that in the definition of the holonomy… That is why it made me wonder whether at the Planck scale it might be the case that you cannot find a local frame of reference in which the description of spacetime can be made isotropic, and hence a modification in the definition of the holonomy would have to be made. But I may be messing things up here!

To define the holonomy of a path we need to pick a direction for that path; the reverse path has the inverse holonomy. It’s fun to think about dropping that last assumption, though.

I understand that the path is oriented but I was thinking about adding more structure to it. Is there a formal difference between an oriented path and a directed path? Thanks.

Christine

Posted by: Christine Dantas on March 15, 2009 2:48 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

On a second thought, now I see that I might be wrong in my reasoning above, but I wait for further clarifications.

Thanks.

Posted by: Christine Dantas on March 15, 2009 3:16 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

$MathML-enabled post (click for more details).$

Christine wrote:

Yes, such lumps may be anisotropic but is it not correct to say that their description can be made mechanically equivalent in the sense that you can always find a local frame of reference in which their description is simpler (isotropic)?

No, unless you’re misusing ‘local’ to mean ‘infinitesimal’. Take the ellipsoid $x^2 + 2y^2 + 3z^2 = 1$ . No matter how close you look at this surface near the point $(1,0,0)$ , it’s not isotropic: there are preferred directions, namely the principal directions.

Perhaps you’re using using ‘local’ to mean ‘infinitesimal’.

Is there a formal difference between an oriented path and a directed path?

I guess you’ll have to give me formal definitions of these terms for me to know what you’re asking about. I don’t get it.

Posted by: John Baez on March 15, 2009 5:45 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

No, unless you’re misusing ‘local’ to mean ‘infinitesimal’.

Hm. That is disturbing. But a good point… I’ll think about it.

I guess you’ll have to give me formal definitions of these terms for me to know what you’re asking about.

Well, the idea of a directed path or “dipath” comes, as far as I know, from concurrency theory in computer science, that is, by extending some ideas from topology to concurrency models. According to Fajstrup et al.:

We define a local partial order on a topological space; this is an open cover of the space by partially ordered open sets such that the partial orders are closed and they are compatible on intersections. A directed path is then a path, which is locally increasing.

References:

- Dihomotopy Classes of Dipath in the Geometric Realization of a cubical set, L. Fajstrup. In “Spatial Representation: Discrete vs. Continuous Computational Models”, 2005.

- Algebraic Topology and Concurrency, Lisbeth Fajstrup, Eric Goubault, Martin Raussen. (preprint R-99-2008, Dept. of Mathematical Sciences, Aalborg University, Aalborg, Denmark. June, 1999).

Now, about “oriented paths” (“orientable paths”?) there is the usual definition, but I wonder whether it is valid for one dimensional objects/manifolds? Perhaps one would have to parametrize the path and impose that it always increases/decreases for a differential increase of the parameter to make an orientable path? But if this is the case, the difference between it and a dipath eludes me.

I fear to be drifting away from the topic, so feel free to ignore my comment if this is the case!

Christine

Posted by: Christine Dantas on March 15, 2009 9:50 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

who did the animation?

Posted by: jim stasheff on March 13, 2009 2:14 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

$MathML-enabled post (click for more details).$

Greg Egan did it. Check out his page on Klein’s quartic curve, his page on Klein’s quartic equation, and also my page on Klein’s quartic curve, which features animations by him and pictures by various other people.

Posted by: John Baez on March 13, 2009 5:29 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

Are you building a theory of 2-unitary duals? It would be neat to have a monoidal structure to go with it.

Minor point: are morphisms in Vect^n really just n-tuples of linear maps? The analogy with C^n suggests they should be n by n matrices of linear maps.

Posted by: Scott Carnahan on March 15, 2009 4:01 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

$MathML-enabled post (click for more details).$

Scott writes:

Are you building a theory of 2-unitary duals?

We haven’t thought that far ahead! It sounds fun.

Indeed, only while writing this Week’s Finds did I notice that we’re engaged in a grand loop: soon we’ll be studying unitary representations of 2-groups on 2-Hilbert spaces… but 2-Hilbert spaces naturally arise as categories of unitary representations of groups.

So, we’ll be able to study weird things like ‘representations of the Poincaré 2-group on the category of representations of the Poincare group’.

Minor point: are morphisms in $Vect^n$ really just $n$ -tuples of linear maps?

Yes!

The analogy with $\mathbb{C}^n$ suggests they should be $n$ by $n$ matrices of linear maps.

I think you’re mixing up the morphisms in $Vect^n$ with the 2-morphisms in $2Vect$ . Of course such level slips are one reason $n$ -category theory is so fun! Makes me dizzier than an amusement park ride.

Just as a morphism from $\mathbb{C}^n$ to $\mathbb{C}^m$ is an $m \times n$ matrix of elements of $\mathbb{C}$ , a morphism from $Vect^n$ to $Vect^m$ is an $m \times n$ matrix of objects of $Vect$ .

So, morphisms in $2Vect$ are matrices of vector spaces. And this gives the possibility of 2-morphisms between these, which are matrices of linear maps.

Posted by: John Baez on March 15, 2009 4:38 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 274)

$MathML-enabled post (click for more details).$

I wrote:

So, we’ll be able to study weird things like ‘representations of the Poincaré 2-group on the category of representations of the Poincare group’.

Less weirdly, for any group $G$ , the automorphism 2-group $AUT(G)$ should have a representation on the category $Rep(G)$ .

Posted by: John Baez on March 16, 2009 4:02 AM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

March 12, 2009