The n-Category Café

The quick way to see it.

If you have absorbed section 8 then everything more or less follows from the following simple observation (if not jump to the next paragraph right now!):

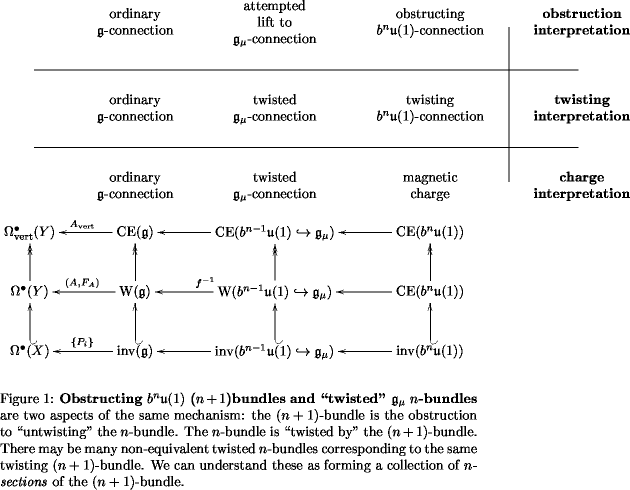
The more expository approach

It will have to be seen how far I can get right now. But it is fun to start with this

Simple reconsiderartion of ordinary electromagnetism aka abelian 1-gauge theory,

as found, with the emphasis we need here, in section 2 of Freed’s article as well as in most every other review of D-brane physics (aka higher generalized electromagnetism aka abelian $n$-gauge theory) like, er, let’s see… p. 111 here:

Clifford Johnson
D-Brane Primer
(arXiv, book homepage).

So the phenomenon of interest here is a generalization to

- a) higher dimensions (meaning higher dimensions of target space);

- b) higher categorical dimensions (meaning higher dimensions of parameter space);

- c) nonabelian structures

of the following high-school facts (well, maybe most highschool don’t teach them this way, which is a pity, because it could easily be taught this way)

So an electromagnetic field on a space $X$ is a closed 2-form

$$F \in \Omega^2_{closed}(X) \,.$$

If there are electrons zipping around on $X$, then the fact that they are charged under the electromagnetic field means that whenever they trace out closed curves $\gamma$ in $X$, we can consistently assign a phase

$$\mathrm{tra}(\gamma) \in U(1)$$

to that curve, an element in $U(1)$, with the property that whenever

$$\gamma = \partial \Sigma$$

is the boundary of a disk $\Sigma$, we have $$\mathrm{tra}(\gamma) = \mathrm{tra}(\partial \Sigma) = \exp(2\pi i \int_\Sigma F) \,.$$

This implies that $F$ is actually integral, meaning that its integral over any closed surface in $X$ is an integer:

$$\partial \Sigma = \emptyset \;\; \Rightarrow \;\; \int_\Sigma F \in \mathbb{Z} \,.$$

From this one concludes that $F$ is in fact the curvature of a line bundle $P \to X$ with connection on $X$.

[An important special case is $X = S^2$ and $P$ the Hopf bundle $S^3 \to S^2$. As Jim Stasheff emphasises, it is the most remarkable fact about the history of science that P. A. M. Dirac found this line bundle from the physics perspective descibed here in the very same year, 1931, that Hopf described his line bundle – and that this was fully appreciated not until decades later (Jim says by Greub and Petry, 1975).]

The electrons zipping around on $X$ produce themselves an electromagnetic field. It turns out that this affects the electromagnetic line bundle we are talking about by the constraint that

$$d \star F = j_E \,,$$

where

$$\star : \Omega^{n+1}(X) \to \Omega^{d-n-1}(X)$$

is the Hodge star operator induced from a choice of (pseudo-)Riemannian metric on $X$; and

$$j_E \in \Omega^3_{closed}(X)$$

is a 3-form which is Poincaré dual to the curves that our electrons trace out.

Electrons are electrically charged. What happens when magnetically charged particles also zip around on $X$ (like the two ends of an ideal current-carrying coil (not to mention just yet the two ends of a string))?

It turns out that in that case there is another 3-form, $j_B$, such that now

$$d F = 0$$

is replaced by

$$d F = j_B \,.$$

Now, that should be a little shocking. A moment ago we had luckily identified two major concepts in physics and math – electromagnetic fields and line bundles with connection. That identification breaks down as be allow nonvanishing $j_B$! The curvature 2-form of a line bundle with connection has no chance but to be closed.

So what’s going on? What is the mathematical structure which is to $d F = j_B$ like ordinary line bundles with connection are to $F \in \Omega^2_{closed}(X)$?

The answer is: twisted bundles.

And strikingly: twisted bundles are really 2-bundles. There is 2-categorical physics around already in 1931, secretly.

And there is an easy way to understand this heuristically: I just mentioned that we get magnetic charges from ideal (infinitely thin) current carrying coils on $X$ – which look like strings. 2-Particles. As they move, they trace out a 2-dimensional volume, not just a curve. So they naturally couple to a 2-bundle!

Which 2-bundle could that possibly be? Easy: the line 2-bundle whose curvature 3-form is just the current 3-form

$$j_B \in \Omega^3_{closed}(X) \,.$$

Which incidentally implies that

a) - the current 3-form has to be integral, too

$$j_B \in \Omega^3_{closed, integral}(X)$$

which incidentally means that “charge is quantized”: it comes in integr multiples of a fixed unit;

b) since it satisfies $d F = j_E$, it must come from a 2-bundle/1-gerbe whose class in $H^3(X,\mathbb{Z})$ is “pure torsion” (vanishes when multiplied with some finite integer).

The math language for electromagnetic fields in the presence of magnetic charge is hence

The magnetic charge is a line 2-bundle which is trivialized by the electromagnetic field, which is a “twisted 1-bundle” or “gerbe module”.

I’ll say more about what this really means later. For the moment, I just want to collect the items in a dictionary relating math and physics here.

Suppose $X$ is $d$-dimensional. And suppose we are talking about electrically charged $n$-particles (known as ($n-1$)-branes). Then

An

electrically charged $n$-particle

on $X$, known as a

electrically charged $(n-1)$-brane

couples to an

electromagnetic $n$-bundle with connection

on $X$, with

curvature $(n+1)$-form $F \in \Omega^{n+1}(X)$

also known as a

$(n-1)$-gerbe with connection and curving

which is “twisted” by a

magnetic charge $(n+1)$-bundle

with curvature $(n+1)$-form

$j_B \in \Omega^{n+2}_{closed}(X)$ known as the magnetic current.

And we get the analogous story with electric and magnetic exchanged everywhere. In fact, it is a coincidence that in the four dimensions which we are familiar with, electrically charged particles correspond also to magnetically charged particles. In other dimensions that fails.

For $d$ dimensional $X$, we have that:

if an electrically charged $n$-particle couples to a field with

curvature $(n+1)$-form $F \in \Omega^{n+1}(X)$

then the Hodge dual form

$$\star F \in \Omega^{d-n-1}(X)$$

may happen to be the curvature $(d-n-1)$-form of

a $(d-n-2)$-bundle with connection which couples to

$(d-n-2)$-particles.

These latter we then call “magnetically charged”.