The n-Category Café

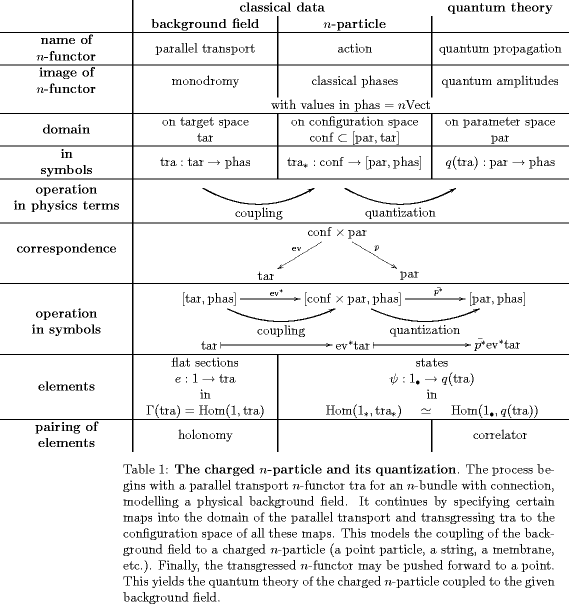
The following table indicates the nature of “twists” on the classical side and of “holography” on the quantum side:

Here is how morphisms of $n$-functors look themselves like $(n-1)$-functors with values in “cylinders”:

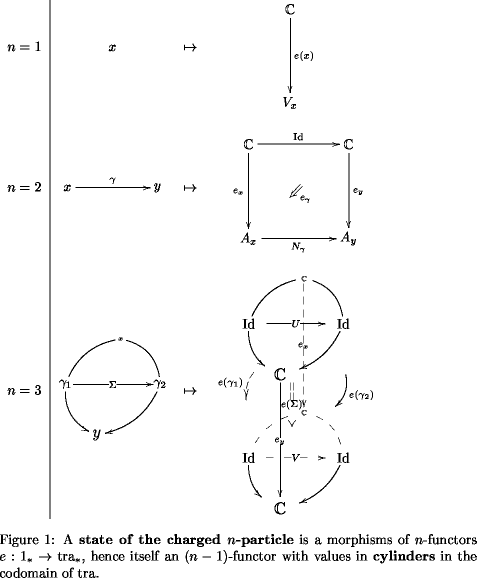
Recall the general relation of sections and states, from this point of view, as discussed in QFT of charged $n$-particle: Definition

Classical Example: Twisted Bundles.

On the classical side, a crucial example is that of a gerbe module, otherwise known as a twisted bundle. That morphisms from the tensor unit into a line 2-bundle (which is the 2-bundle version of a bundle gerbe) are gerbe modules is discussed in Quantum 2-States: Sections of 2-vector bundles.

This gives rise to the phenomenon that when quatizing the 2-particle (the string) charged under a Kalb-Ramond field by pushing its classical parallel transport 2-functor to a point, we find that the “2-space of 2-states” over the endpoints does correctly reproduce the coupling of the string to these gerbe modules, known in this context as D-branes with Chan-Paton bundles.

Spin Structures, String Structures, etc., as vanishing of twists.

In the above example, the bundle which arises as a morphism into the gerbe from the tensor unit is untwisted (an ordinary bundle) precisely if the gerbe is trivializable. Then the morphism establishes precisely the trivialization.

So we can express the vanishing of certain obstructions this way.

Let $P \to X$ be an $SO(n)$ bundle over $X$. In general it may not be lifted to a $\mathrm{Spin}(n)$-bundle along the extension $\mathbb{Z}_2 \to \mathrm{Spin}(n) \to SO(n)$.

But we may conceive $\mathrm{SO}(n)$ as the strict 2-group $(1 \to SO(n))$. And we have an equivalence $$(\mathbb{Z}_2 \to \mathrm{Spin}(n)) \stackrel{\sim}{\to} (1 \to \mathrm{SO}(n)) \,.$$ Hence we can lift any $\mathrm{SO}(n)$-bundle to a $(\mathbb{Z}_2 \to \mathrm{Spin}(n))$-2-bundle.

On triple overlaps this defines a $\mathbb{Z}_2$-gerbe, a $(\mathbb{Z}_2 \to 1)$-2-bundle. This gerbe is trivializable precisely if the original bundle admited a lift to a spin bundle. And we detect if the 2-bundle is trivial by checking if it has an isomorphism to the triviail such 2-bundle: a global 2-section.

Similar constructions work fro $\mathrm{String}$-structures:

Not every $\mathrm{Spin}(n)$-bundle may be lifted to a $\mathrm{String}(n)$-bundle. But every $(1 \to \mathrm{String}(n))$-2-bundle is a $(\Omega \mathrm{Spin}(n) \to P \mathrm{Spin}(n))$-2-bundle, since the two 2-groups are equivalent. And this in turn is the same as a $(U(1) \to \hat \Omega \mathrm{Spin}(n) \to P \mathrm{Spin}(n))$-3-bundle.

On top level, this 3-bundle is an abelian 3-bundle (a Chern-Simons gerbe). If this trivializes, i.e. if we can find a global section, then we have constructed a $\mathrm{String}(n)$-lift of the original $\mathrm{Spin}(n)$-bundle.

Stephan Stolz and Peter Teichner have explicit constructions of $n$-vector bundles for these situations, which correspond, as far as I could see, to the above principal $n$-bundles by associating $n$-vector bundle to principal $n$-bundles by means of $n$-representations.

CFT and Chern-Simons theory.

One big question is how studying extended 2-dimensional rational conformal field theory in terms of certain functors $$2\mathrm{Cob} \to 2\mathrm{Vect}$$ reproduces the description of rational CFT in terms of the FRS formalism. (See also the FRS Theorem).

My main point which I have been discussing for a while now is that

The FRS decoration prescription is the result of choosing a local trivialization of a global CFT 2-transport functor and expressing the latter locally in terms of transition data.

That’s why it’s so similar to the expression of surface holonomy for a gerbe in terms of local data: in both cases we are expressing a globally defined 2-functor in terms of local data and gluing data.

I started working out how the local trivialization of a 2-functor with values in certain bimodules leads to the decoration prescriptions as found in the FRS formalism in FRS Formalism from 2-Transport.

In that document, I am simply assuming that the bimodules appearing all are “induced bimodules”. This is a crucial ingredient in the FRS formalism.

Later I realized that this fact can be understood nicely by conceiving the extended QFT not just as any 2-functor with values in bimodules, but in fact as a 2-functor that arises as a natural transformation of two 3-functors: the 2-functor is really holographically related to a Chern-Simons 3-functor.

Namely, the 2-category of “induced bimodules” arises precisely as the 2-category of cylinders in the 3-category $\Sigma \mathrm{Bim}$. This is the main point at the end of The 1-dimensional 3-vector space.

As noticed at the end of D-Branes from Tin Cans, III: Homs of Homs, the cylinders in $\Sigma \mathrm{Bim}$ which one obtains by considering (“holographically”) morphisms of locally trivial 3-functors with values in 3-vector spaces (like in Chern-Simons theory)

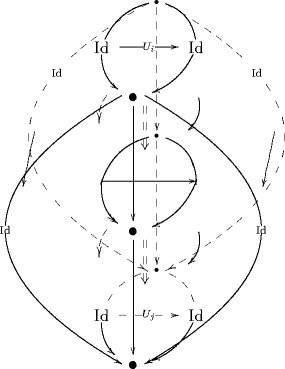
are to be thought of as nothing but the diagram as appearing for instance on p. 10 of

Topological and conformal field theory as Frobenius algebras.

The Poincaré-dual string diagram version of this cylindrical 3-morphism in $\Sigma \mathrm{Bim}$ yields the ribbon decoration of this situation as found on p. 33 of TFT construction of RCFT correlators IV: Structure constants and correlation functions.

So, not only can we understand the FRS decoration prescription as a local trivialization of a 2-functor, but we can also understand this 2-functor as arising as the transformation of locally trivial TFT 3-functors.

If you look at these pictutres, they suggest a natural relation to the modular functor and other ingredients here. I started working this out in more detail with Jens Fjelstad, but much still needs to be done. I am hoping to meet Jens again in a month or so, to bring this to a more developed stage.

Anyway, that’s how I see the relation between 3-dimensional TFT and 2-dimensional CFT. Stephan Stolz and Peter Teichner are now working on a closely related picture.