The Algebra of Grand Unified Theories II
Posted by John Baez
I started out using this blog entry as a plea for people to help improve the following paper… but now it’s a lot better, so we put it on the arXiv:
- John Baez and John Huerta, The Algebra of Grand Unified Theories.
This fills in the details for John Huerta’s talk.
The goal of the paper is to take mathematicians who know just a bit about groups and their representations, and gently teach them a bit of particle physics — just enough so they can appreciate the meaning of this cube:
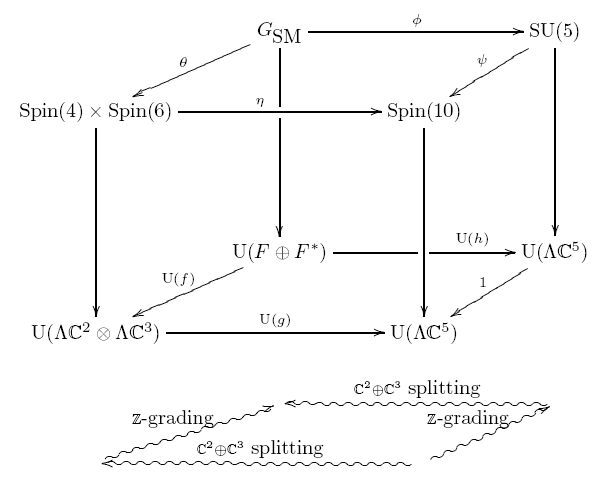
This cube summarizes the relation between four theories of physics. The symmetry groups of these theories lie at the cube’s top corners. Each of these groups acts on each generation of fermions and their antiparticles via a unitary representation on a 32-dimensional Hilbert space. These representations are the vertical arrows in the cube. The rest of the arrows are group homomorphisms that make the whole cube commute!
Here are the four theories:
-
The Standard Model of particle physics. The symmetry group here is SU(3) SU(2) U(1), denoted for short in the cube above. This group acts on the fundamental fermions and their antiparticles via a unitary representation on the 16-dimensional Hilbert space , which describes one generation of fermions: quarks and leptons. It also acts on the dual space , which describe the antiparticles of these fermions. So, it acts on , and this representation is the unlablled vertical arrow at the back left. The precise formula for this representation seems incredibly complicated and arbitrary.
In short: the Standard Model looks like a mess.
-
The SU(5) theory proposed by Georgi and Glashow. There is a beautiful homomorphism SU(5), which is almost one-to-one: its kernel has just 6 elements! And amazingly, this fact naturally ‘explains’ the complicated representation that appears in the Standard Model. More precisely: there’s an obvious representation of SU(5) on the exterior algebra , which is the unlabelled vertical arrow at the back right of the cube. There’s also isomorphism of Hilbert spaces , which gives the horizontal arrow . And, the back square of the cube commutes! This means the complicated vertical arrow at the back right can be expressed in terms of the obvious representation of SU(5) on the exterior algebra .
In short: the Standard Model looks a lot more elegant when embedded in the SU(5) theory.
-
The Spin(10) theory proposed by Georgi. Using the fact that a 5-dimensional complex vector space can be seen as a 10-dimensional real vector space, we can see SU(5) as a subgroup of Spin(10). The representation of SU(5) on is highly reducible, but it extends to a representation of Spin(10) on the same space, called the ‘Dirac spinor representation’. This representation is the unlabelled vertical arrow at the front right of the cube. This representation is almost irreducible: it breaks up into just two pieces, one for particles and one for antiparticles.
In short: we can unify all the particles in one generation of fermions by going from SU(5) to the bigger group Spin(10).
-
The Spin(4) Spin(6) theory proposed by Pati and Salam. By what I’ve said, the Standard Model symmetry group is a subgroup of Spin(10). But in fact, it’s a subgroup of the smaller group Spin(4) Spin(6). Just as Spin(10) has a Dirac spinor representation on , the groups Spin(4) and Spin(6) have Dirac spinor representations on
and , respectively. These combine to give the vertical arrow at the front left. And we can define maps that make the left face of the cube commute!
In short: the Standard Model also looks a lot simpler in terms of the Pati–Salam model.
Furthermore, there are obvious maps making the front of the cube commute. In fact, the whole cube commutes. This means that in a certain sense, the Spin(10) theory extends both the SU(5) theory and Pati–Salam model in a consistent way!
What are the wiggly arrows beneath the cube, you ask?
These convey the overall moral message:
The group Spin(10) acts as unitary transformations of the exterior algebra . SU(5) is precisely the subgroup that preserves the grading on this exterior algebra. On the other hand, Spin(4) Spin(6) is the precisely the subgroup that preserves the splitting of as . And the Standard Model gauge group is the subgroup that preserves both the grading and the splitting.
If none of this makes sense except the math words like ‘unitary representation’ and ‘exterior algebra’, don’t be intimidated! You’re probably just the sort of person who should read our paper. It’s much more gentle than the blast of information I just delivered.



Re: The Algebra of Grand Unified Theories II
Hey, cool. Here are my notes so far as I read through it:
p1
First sentence is a bit redundant.
”dark matter” quotes got reversed.
The first two paragraphs seem a little awkward. But Connes will be happy for the mention.
p2
“none of these attempts at unification are considered plausible today.” Is that true? I thought many physicists were still pretty keen on SO(10).
“all three theories require certain trends to hold among coupling constants (numbers which determine the relative strengths of forces) that the data do not support.” Hmm, the coupling constant convergence is actually pretty good even without supersymmetry; all you have to do to get them to meet perfectly is throw in a few more Higgs particles.
“remains a mystery without a solution” redundant.
Jump between last two paragraphs is a bit abrupt. Could probably omit the description of Heisenberg’s model.
p3
“the gauge group of the Standard Model in some larger group G, and we will give G a representation
V which reduces to the Standard Model representation F⊕F∗ when we pullback to GSM along this inclusion.” This is a summary of the main idea, so it could probably be repeated with an expanded description in more basic language.
“the Standard Model is precisely the theory that reconciles the two visions of physics lying behind the SU(5) theory and the Pati–Salam model.” Neat, if a bit of a random observation. But, hmm, what about the right handed neutrino that’s missing from the SU(5) model? Guess you could include it as a singlet.
p5
Could probably get rid of the example of two particles on a line and just use the Hilbert space of proton and neutron after they’re introduced.
Are all mathematicians familiar with bra ket notation? Maybe define these things as states, or omit that part.
p6
Overall, that was a nice introduction to isospin.
Why not introduce the Pauli-matrices here, and the proton and neutron and their I_3 values as eigenvectors and eigenvalues (weights) under sigma_3? That would make it much more clear what these charges are.
p7
Pion interactions are nice. Why not describe Pions as being eigenvectors in complex su(2)?
p8
“in terms mass and”
p9
Continue to like the use of Feynman diagrams.
p10
Nice segue to quarks.
In the tables, why not just label the column “EM charge” instead of having an EM column with “yes“‘s in it?
“quark confinement, is still somewhat mysterious” Ooh, Gross, Wilczek, and Politzer are going to be pissed.
“the a first-generation”
Hmm, maybe put those three colored quarks in a column, so people can see its operated on by su(3) just like the proton and neutron were in a 2 column.
p11
Hmm, isn’t a proton “different” depending on what color its down quark is? (This point is probably academic.) If so, those states written middle page for the proton and neutron seem a little weird.
Ah, nice way to relate isospin to weak isospin. (Hmm, sometimes you see isospin relating u, d, and s… but maybe that’s long forgotten.)
(gotta go, dinner calls…)