New Structures for Physics III

February 27, 2009

Posted by John Baez

$MathML-enabled post (click for more details).$

Here’s a new improved version of a paper for Bob Coecke’s book New Structures for Physics:

John Baez and Mike Stay, Physics, topology, logic and computation: a Rosetta Stone — 4th draft version or arXiv version.

We thought it was done almost a year ago, but there was a serious mistake at the very end of the section on computation. Now we’ve completely rewritten that section — so, we’d love to hear what you think about it. Typos? Fine, we’ll fix them. Serious mistakes? I hope not, but if so, please tell us about them now!

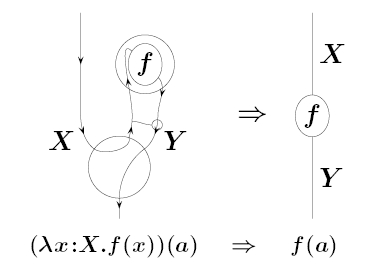
$MathML-enabled post (click for more details).$

The mistake, in case you’re wondering, was in our discussion of a programming language that was supposed to perfectly reflect what you can do in a symmetric monoidal closed category. Luckily, we found that Simon Ambler had invented such a language in his thesis:

Simon Ambler, First order linear logic in symmetric monoidal closed categories, Ph.D. thesis, U. of Edinburgh, 1991. Also available in gzipped Postscript from his homepage.

So, we decided to explain that! This required massive revisions of the whole ‘computation’ section of our paper.

Luckily, we had a year to do this. That’s because another person writing a paper for Bob’s book was also late. When he finished his contribution, we had to hurry up and finish ours.

I don’t want to name names, but this other person’s paper is really great:

Peter Selinger, A survey of graphical languages for monoidal categories.

Abstract: This article is intended as a reference guide to various notions of monoidal categories and their associated string diagrams. It is hoped that this will be useful not just to mathematicians, but also to physicists, computer scientists, and others who use diagrammatic reasoning. We have opted for a somewhat informal treatment of topological notions, and have omitted most proofs. Nevertheless, the exposition is sufficiently detailed to make it clear what is presently known, and to serve as a starting place for more in-depth study. Where possible, we provide pointers to more rigorous treatments in the literature. Where we include results that have only been proved in special cases, we indicate this in the form of caveats.

It nicely complements our paper and also this one by Coecke and Paquette, which will appear in the same book:

Bob Coecke and Eric Oliver Paquette, Categories for the practicing physicist.

All three papers tackle the theme of ‘string diagrams’ as tools for reasoning in monoidal categories — but they take quite different angles. Together they cover the subject pretty thoroughly.

Posted at February 27, 2009 4:24 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1921

35 Comments & 0 Trackbacks

Re: New Structures for Physics III

Quibble:
At the bottom of page 9, you say that only topology matters. I think what you mean is that only the relative order of the critical points matters. Latter with the tensorator, you might relax this condition. But right now, the tangles are going to be composed of cups caps, tensor products, and “straight” strings.

Posted by: Scott Carter on February 27, 2009 5:04 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

On page 9 we’re talking about a 1-category of tangles, so what we say is true: only the topology matters, not the relative heights of critical points.

If we got into studying a 2-category of tangles, then yes: certain tangles we’re treating as equal would instead be treated as isomorphic.

But this paper has very little to say about $n$ -categories. There are just two points where we hint that the whole story we’re telling — the story of how closed monoidal categories unify certain aspects of physics, topology, logic and computation — is just the start of a bigger $n$ -categorical story!

The first is on page 24, where we display the Periodic Table and say:

An $n$ -category has not only morphisms going between objects, but 2-morphisms going between morphisms, 3-morphisms going between 2-morphisms and so on up to $n$ -morphisms. In topology we can use $n$ -categories to describe tangled higher-dimensional surfaces, and in physics we can use them to describe not just particles but also strings and higher-dimensional membranes. The Rosetta Stone we are describing concerns only the $n = 1$ column of the Periodic Table. So, it is probably just a fragment of a larger, still buried $n$ -categorical Rosetta Stone.

The second is on page 54, in the intro to the section on computation, where we say:

Quite roughly speaking, a ‘typed lambda-theory’ is a very simple functional programming language with a specified collection of basic data types from which other more complicated types can be built, and a specified collection of basic terms from which more complicated terms can be built. The data types of this language are objects in a cartesian closed category, while the programs — that is, terms — give morphisms!

Here we are being a bit sloppy. Recall from Section 3.3 that in logic we can build closed monoidal categories where the morphisms are equivalence classes of proofs. We need to take equivalence classes for the axioms of a closed monoidal category to hold. Similarly, to get closed monoidal categories from computer science, we need the morphisms to be equivalence classes of terms. Two terms count as equivalent if they differ by rewrite rules such as beta reduction, eta reduction and alpha conversion. As we have seen, these rewrites represent the steps whereby a program carries out its computation. For example, in the original ‘untyped’ lambda calculus, the terms $times(\overline{3})(\overline{2})$ and $\overline{6}$ differ by rewrite rules, but they give the same morphism. So, when we construct a cartesian closed category from a typed lambda-theory, we should work with a cartesian closed 2-category which has:

types as objects,

terms as morphisms,

equivalence classes of rewrites as 2-morphisms.

For details, see the work of Seely, Hilken and Melliès. Someday this work will be part of the larger $n$ -categorical Rosetta Stone mentioned at the end of Section 2.5

This business of going from a 1-category to 2-category to better understand computation is precisely analogous to going from a 1-category to a 2-category to better understand tangled surfaces… as explained here.

But the point of this Rosetta Stone paper is to draw in a bigger audience at the ground floor, not take an elevator ride up the tower of $n$ -categories!

Posted by: John Baez on February 28, 2009 1:35 AM | Permalink | Reply to this

Re: New Structures for Physics III

Forgive me the poor quality of my english. Just an historical information : Heyting algebras (a.k.a as “Brouwerian algebras”) were not introduced by Heyting, but rather by polish logicians just after world war 2.

See (for example !):

Some Theorems About the Sentential Calculi of Lewis and Heyting
Author(s): J. C. C. McKinsey and Alfred Tarski
Source: The Journal of Symbolic Logic, Vol. 13, No. 1 (Mar., 1948), pp. 1-15

Proofs of Non-Deducibility in Intuitionistic Functional Calculus
Author(s): Andrzej Mostowski
Source: The Journal of Symbolic Logic, Vol. 13, No. 4 (Dec., 1948), pp. 204-207

Rasiowa H.
(1951) Algebraic treatment of the functionnal calculi of Heyting and Lewis, Fundamenta Mathematicae, vol.38, pp. 19-126

Posted by: Jean Fichot on April 6, 2010 8:33 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Some typos:

p. 37: “we can define $\not X$ to be $X \Rightarrow F$ ” ( $F$ sticks out as you write $\bottom$ everywhere else)

p. 43: “a neutron can turn into a neutrino together with a proton and an electron” (I suppose $\nu*$ is meant to be an antineutrino)

p. 55: “times(3) is a program that multiplies by 2”

Posted by: Gabriel Ebner on February 27, 2009 9:44 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Thanks, Gabriel! Those last two are downright embarrassing!

They’re fixed now.

Posted by: John Baez on February 28, 2009 1:01 AM | Permalink | Reply to this

Re: New Structures for Physics III

I believe I have found another typo.
Pg 25:
“For example, … then X -o Z is just the set of functions from Y to Z” (presumably should be X to Z)

Posted by: Bryn Rahm on March 2, 2009 4:52 AM | Permalink | Reply to this

Re: New Structures for Physics III

Thanks! You’re right!

Posted by: John Baez on March 2, 2009 6:07 AM | Permalink | Reply to this

Re: New Structures for Physics III

Interesting paper. Nice overview of a various domains and a good set of references. Thanks.

I think it does a good job of making its point (convinced me anyway:) - there are deep structural parallels between (at least an interesting subset of) these subjects that can be described by specific categories.

I suppose this is a bit subjective but I am not sure I would say that Algol was the first computer science profit from lambda calculus (bottom of pg 52).

John McCarthy’s Lisp (1958 - original paper online link - http://www-formal.stanford.edu/jmc/recursive.html) was conscientiously modeled on lambda calculus.

While influenced by Lisp, Algol is most notable really as the first ‘modern’ imperative language. It is the progenitor of BASIC, C (Java etc) (but preceded by Fortran).

Also a small editorial comment. The sentence on pg 38 ‘Unfortunately, since we have decided to study ^ and T but not their mirror partners V and (bot), this duality will
not be visible in the sections to come.’ reads (to me anyway) a bit like ‘Unfortunately, since we’ve decided to poke ourselves in the eye with a stick, we will not be able to use stereoscopic vision’. (‘Doctor it hurts when I do this.’ ‘Well don’t do that.’) You do earlier mention that logicians like to study simpler systems but perhaps a sentence explicitly saying why this particular omission?

Perhaps more ‘speculative’ applications of this relation might be of interest?

Probably out of place in this paper but a (cafe?) discussion around ‘why is there is parallel’ could also be interesting.

Posted by: Bryn Rahm on March 1, 2009 3:52 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Bryn wrote:

Interesting paper.

Thanks. I’m glad you liked it, and even more I’m glad you found its main point convincing.

I suppose this is a bit subjective but I am not sure I would say that Algol was the first computer science profit from lambda calculus (bottom of pg 52).

John McCarthy’s Lisp (1958 - original paper online link - http://www-formal.stanford.edu/jmc/recursive.html) was conscientiously modeled on lambda calculus.

Thanks! I didn’t really say ALGOL was the first way computer science profited from the lambda calculus, but I said something equally false, namely: “It took even longer for computer scientists to profit from Church and Kleene’s insights. This began in 1965, when Landin pointed out a powerful analogy between the lambda calculus and the programming language ALGOL. Landin’s paper was very influential. It led to a renewed burst of work on the lambda calculus which continues to this day.” I thought Landin’s paper on ALGOL was the first place where someone noticed the relevance of the lambda calculus to the practice of programming — I read something like this somewhere. I thought Lisp came later. But while Landin’s paper was probably influential, I now see that Lisp came first!

The sentence on pg 38 ‘Unfortunately, since we have decided to study $\wedge$ and $\top$ but not their mirror partners $\vee$ and $\bottom$ , this duality will not be visible in the sections to come.’ reads (to me anyway) a bit like ‘Unfortunately, since we’ve decided to poke ourselves in the eye with a stick, we will not be able to use stereoscopic vision’. (‘Doctor it hurts when I do this.’ ‘Well don’t do that.’) You do earlier mention that logicians like to study simpler systems but perhaps a sentence explicitly saying why this particular omission?

The reason is that the paper is about closed monoidal categories and how they show up in physics, topology, logic and computation. In logic, we can think of propositions as forming a closed monoidal category with $\wedge$ (“and”) as tensor product and $\top$ (“true”) as the unit… but if we include $\vee$ (“or”) and $\bottom$ (“false”) we get a richer sort of category that goes beyond the scope of this paper.

Someday I would enjoy writing about how this bigger story plays itself out in physics, logic, topology and computation. But, not here!

Perhaps more ‘speculative’ applications of this relation might be of interest?

This paper was meant in part as way of educating ourselves about some things before diving into deeper waters. My main interest is in categorifying the whole story in this paper… and that’s part of what Mike’s thesis will be about.

Probably out of place in this paper but a (cafe?) discussion around ‘why is there is parallel’ could also be interesting.

Indeed, that’s a question I find fascinating. Briefly put, I think the universe is made of things and processes — or at least, that’s how we parse it. Things and processes can be seen as ‘objects’ and ‘morphisms’, so category theory is a powerful unifying tool. In quantum physics we draw processes as ‘Feynman diagrams’; in general relativity we call processes ‘spacetimes’; in logic we call them ‘proofs’; in computer science we call them ‘programs’. But, we think about all four the same way, and indeed there’s not a sharp distinction between them. I want to get to the point where I can see clearly how they’re the same and how they’re different. And then I want people to use this insight to do amazing things.

Posted by: John Baez on March 1, 2009 7:25 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

The reason is that the paper is about closed monoidal categories and how they show up in physics, topology, logic and computation. In logic, we can think of propositions as forming a closed monoidal category with $\wedge$ (“and”) as tensor product and $\top$ (“true”) as the unit… but if we include $\vee$ (“or”) and $\bot$ (“false”) we get a richer sort of category that goes beyond the scope of this paper.

You can explain this purely in logical terms by noting that not only are you studying $\wedge$ and $\top$ , you're also studying their interaction with $\Rightarrow$ , and that breaks the symmetry already.

(At least, it breaks the symmetry in intuitionistic logic. In classical logic, where $p \Rightarrow q \equiv \neg{p} \vee q$ , this is paired with $\setminus$ , where $p \setminus q \equiv p \wedge \neg{q}$ classically. However, classical logic cannot be categorified in a nontrival but first-order way. Of course, you could switch over to dual-intuitionistic logic, which has $\setminus$ but not $\Rightarrow$ ; then you would be discussing closed cocartesian categories, but that is simply the same subject with dual notation.)

Posted by: Toby Bartels on March 1, 2009 9:53 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

However, classical logic cannot be categorified in a nontrival but first-order way.

That’s a very sweeping statement; what exactly do you mean by it? Do you just mean that any cartesian closed category in which $0^{0^A}\cong A$ for all $A$ is a poset (hence a Boolean algebra)? That’s certainly true, but there are other ways to categorify things.

Posted by: Mike Shulman on March 2, 2009 3:54 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Of course, ‘categorify’ is a vague term, but we normally expect to be able to decategorify by considering objects only up to their isomorphisms classes, and if we're to get a boolean algebra after doing that, then we would need $0^{0^A} \cong A$ .

But yeah, there are other ways, so I mean other precise statements like that every boolean pretopos is a topos (so higher order).

Perhaps you would argue that a boolean category by itself is already a good categorification of classical logic? All right, I'll accept that.

Posted by: Toby Bartels on March 3, 2009 9:06 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

If a topos is disallowed because it’s higher-order, then so should be a cartesian closed category.

Yes, from one perspective a Boolean category is also a categorification of classical logic. Also, in any $\Pi$ -pretopos (or less, probably), we have $0^{0^A} \cong \neg\neg supp(A)$ . Thus if $Sub(1)$ is a Boolean algebra and supports split (such as in $Set$ ), we have morphisms $A\to 0^{0^A}$ and $0^{0^A}\to A$ , so that if we then pass to the poset-reflection (also a reasonable way to decategorify, especially from the propositions-as-types perspective) we obtain a Boolean algebra.

From a totally different perspective, I think I recall that classical linear logic can be nontrivially categorified.

Posted by: Mike Shulman on March 3, 2009 5:57 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

OK, you've got a good point about the poset reflection.

But $\Pi$ is justified as a categorification of for $\forall$ (again, especially from a perspective of propositions as types), whereas power objects are a new higher-order ingredient.

And don't get me started on ‘intuitionistic’ vs ‘classical’ linear logic. There's nothing classical about classical linear logic; that's just fetishising a feature of how Gentzen chose to write sequent calculus.

Posted by: Toby Bartels on March 3, 2009 8:17 PM | Permalink | Reply to this

Re: New Structures for Physics III

And don’t get me started on ‘intuitionistic’ vs ‘classical’ linear logic. There’s nothing classical about classical linear logic; that’s just fetishising a feature of how Gentzen chose to write sequent calculus.

I’m not quite sure what you mean. Ignoring sequent calculus and how it’s presented, it always seemed plain to me that ‘classical’ here refers to taking negation to be involutory, which is consonant with how the word is used in contrasting classical to intuitionistic propositional logic, for example.

Posted by: Todd Trimble on March 3, 2009 9:56 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Ignoring sequent calculus and how it’s presented, it always seemed plain to me that ‘classical’ here refers to taking negation to be involutory, which is consonant with how the word is used in contrasting classical to intuitionistic propositional logic, for example.

That doesn't seem to be how people describe it, but maybe that's just what I've read. Your way makes sense: CLL has involutory negation, while ILL does not.

I still don't find CLL very classical; in particular, it still has a non-involutory intuitionistic negation ( $!A \multimap 0$ IIRC). Indeed, it extends intuitionistic logic by providing finer distinctions, just as IL extends CL by providing distinctions (between $A \vee B$ and $\neg(\neg{A} \wedge \neg{B})$ etc), even though it can be motivated without passing through IL.

Still, to say that this makes it not very classical is perhaps unfair, since the terms ‘classical’ and ‘intuitionistic’ aren't really at the same level. Maybe I should say that I find linear logic, even CLL, very constructive? And that I don't feel the motivation for considering ILL instead of CLL that I do feel for considering IL instead of CL.

Posted by: Toby Bartels on March 3, 2009 10:49 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

it always seemed plain to me that “classical” here refers to taking negation to be involutory

That’s in accord with what I’ve read about linear logic as well.

My impression is that classical linear logic can be viewed as a generalization both of ordinary (“polynomial?”) classical logic and ordinary intuitionistic logic. One might say that CLL finds a way to be “constructive” while still retaining an involutory negation.

Posted by: Mike Shulman on March 4, 2009 1:13 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

I still don’t find CLL very classical; in particular, it still has a non-involutory intuitionistic negation…

[I excised your sentence because I’ve forgotten how to make that darned lollipop symbol.] That’s quite understandable. In the current Baez-Stay context of MILL as modeled by symmetric monoidal closed categories, I was relegating full linear logic (including in particular the operator $!$ ) to the back burner.

Maybe I should say that I find linear logic, even CLL, very constructive? And that I don’t feel the motivation for considering ILL instead of CLL that I do feel for considering IL instead of CL.

Yes, that’s true! The very act of linearizing (that is, removing the “structural” constraints implied by taking products to be cartesian) is what I think was so liberating to Girard: one retains the classical self-dualizing symmetries without sacrificing the constructive aspects. Whereas there’s a kind of bluntness to [I’ll say propositional] CL, which shows up in the fact that a straightforward categorification of Boolean algebras to cartesian *-autonomous categories produces nothing new – which is not at all the case for IL. For logicians, then, what was interesting is that Girard trained his sights on the cartesian aspects as the “culprit”.

Posted by: Todd Trimble on March 4, 2009 1:50 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Mike and Todd wrote:

[I excised your sentence because I’ve forgotten how to make that darned lollipop symbol.]

It's \multimap. Silly, I know, but I guess that somebody saw $A_1 \otimes \cdots \otimes A_n \multimap B$ as the space of multilinear maps from $A_1$ through $A_n$ to $B$ and thought that ‘multi’ was the important part rather than ‘linear’. (Or maybe it has a history that I just don't know.)

One might say that CLL finds a way to be “constructive” while still retaining an involutory negation.

Yeah, I read that all the time. But then when they introduce ILL, they say that they're going to consider only ‘intuitionistic’ sequents (those with only or exactly one item on the right side) and those operators with introduction and elimination rules involving such sequents, and I think both ‹Why?› and ‹What's so ‘intuitionistic’ about that?›. (The motiviation for the smaller fragment MILL, now that I get.)

Interestingly, Wikipedia points me also to ‘full’ ILL; FILL includes $\mid$ (par) and accordingly uses ‘classical’ sequents but still distinguishes $A \multimap B$ from $(A \multimap \bot) \mid B$ . I can undersand that name, but I still wonder why.

The very act of linearizing is what I think was so liberating to Girard.

Yes, ‘liberating’ is right! I get a kind of giddiness when I contemplate linear logic, sort of what I used to get with geometric algebra. It's just got … everything!

Posted by: Toby Bartels on March 4, 2009 7:09 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Aww, does itex/MML not support the actual “par” symbol?

I generally don’t try to ascribe much meaning to the use of “classical” and “intuitionistic” as applied to linear logic; I just regard them as words people have chosen to describe various fragments of it, that don’t necessarily have any real connection to the meanings of “classical” and “intuitionistic” for nonlinear logic.

Yes, ‘liberating’ is right! I get a kind of giddiness when I contemplate linear logic, sort of what I used to get with geometric algebra.

Interesting that you should say that. I suppose that one man’s liberation is another’s straitjacket. I would feel more liberated if I knew a real use for linear logic. Yes, closed symmetric monoidal categories, but they feel more like a model for “linear type theory.” Linear logic feels like it ought to happen in a fibred quantale over a locally closed symmetric monoidal category, but I don’t even know what that means, let alone whether there are any naturally-ocurring examples. And I still haven’t managed to wrap my head around par.

Posted by: Mike Shulman on March 4, 2009 5:45 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Aww, does itex/MML not support the actual “par” symbol?

Unicode supports it, and therefore MathML supports it, but iTeX does not as far as I can see. (AMS-TeX doesn't support it, so I wouldn't expect iTeX to support it, although all that I know for sure is that \par doesn't work.)

But if you want it, here it is: ⅋. And in math mode: $A \multimap B \equiv A^\perp ⅋ B$ although that is not technically correct (since iTeX didn't know that this strange Unicode symbol was for an operator), so I copy and past the compiled MathML and fix it here: $A ⊸ B \equiv A^{⊥} ⅋ B$ which frankly looks worse to me, but that's probably Firefox's fault.

Posted by: Toby Bartels on March 5, 2009 1:35 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Toby wrote:

But if you want it, here it is: ⅋.

In case anyone is wondering and not clever enough to figure it out, that’s

⅋

in HTML. If I type that string of symbols in this comment you see this:

⅋

If I just cut and paste what Toby wrote, you see:

⅋

which seems to be fine too.

A puzzle: why do logicians call this operation ‘par’?

Posted by: John Baez on March 6, 2009 8:13 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

in HTML

Actually, in SGML, which is more general than the XHTML (not HTML exactly) and MathML that these pages use. I mean, to be technical about it.

A puzzle: why do logicians call this operation ‘par’?

In one of the many useful metaphors for linear logic, $A | B$ (I'm going back to what iTeX can do for ease of typing) refers to programs $A$ and $B$ being run in parallel however the compiler or operating system chooses as the best allocation of resources. Whereas $A \otimes B$ is the same programs being run at the direction of the programmer or user, with the possibility that they run independently but also that one waits for the other to finish and uses its result (or even more complicated back-and-forth interaction). Not that the compiler or operating system is unable to make similar judicious choices, but it's all behind the scenes.

Similarly, $A \oplus B$ is $A$ or $B$ (not both) at the discretion of the compiler or operating system, while $A \& B$ ( $A$ ‘with’ $B$ ) gives that choice to the programmer or user. Also, $?A$ has the computer choose how many times (if at all) to run $A$ in par-like parallel, while $!A$ leaves all that up to the human once more. To complete the list of symbols (if not the explanation), the respective identities of $|$ , $\otimes$ , $\oplus$ , and $\&$ are $\bot$ , $1$ , $0$ , and $\top$ . This metaphor (like many others) is not that good at showing the difference between $\bot$ and $1$ .

Posted by: Toby Bartels on March 7, 2009 2:14 AM | Permalink | Reply to this

New symbols for Physics

$MathML-enabled post (click for more details).$

$$
 A\multimap B\equiv A^\perp \mathop{&#8523;}B
$$

produces

$A\multimap B\equiv A^\perp \mathop{⅋}B$

while correctly treating ⅋ as an operator.

It required upgrading to the latest Comprehensive LATEX Symbol List to discover that there actually is a LaTeX font (cmll) which has this symbol, and that the associated macro is \parr (not \par).

Is this something that should be added to itex2MML?

Posted by: Jacques Distler on March 7, 2009 4:55 AM | Permalink | PGP Sig | Reply to this

Re: New symbols for Physics

$MathML-enabled post (click for more details).$

A\multimap B\equiv A^\perp \mathop{⅋}B

Cool. But am I the only one (Firefox 3 on Ubuntu) who finds that the spacing is larger when it's not correctly an operator?

\parr (not \par)

Now that you say that, it's obvious that they can't use \par, since that's already a paragraph break in TeX.

Is this something that should be added to itex2MML?

In principle yes, but I think that the priority is low.

Posted by: Toby Bartels on March 7, 2009 7:25 AM | Permalink | Reply to this

Re: New symbols for Physics

$MathML-enabled post (click for more details).$

My CLSL says that there’s also txfonts/pxfonts that has it as \invamp. I haven’t used either though.

The spacings look almost indistinguishable to me (also Firefox 3 on Ubuntu), although Toby’s “operator” version might have a little less space. Jacques’ “operator” version has more space than Toby’s though, and looks fine to me; its generated MathML includes an extra lspace="0em" rspace="thinmathspace".

Posted by: Mike Shulman on March 7, 2009 4:39 PM | Permalink | Reply to this

Re: New symbols for Physics

$MathML-enabled post (click for more details).$

My CLSL says that there’s also txfonts/pxfonts that has it as \invamp.

Ah. Well that’s more promising. We already load the txfonts for some characters. And I know most modern LaTeX distributions include them.

So …

$$
A \invamp B = B\parr A
$$

$A \invamp B = B\parr A$

works here, now (and at ncatlab.org)

Posted by: Jacques Distler on March 8, 2009 1:40 AM | Permalink | PGP Sig | Reply to this

Re: New Structures for Physics III

Linear logic feels like it ought to happen in a fibred quantale over a locally closed symmetric monoidal category, but I don’t even know what that means, let alone whether there are any naturally-ocurring examples.

Quite a long time ago, Rick Blute had a manuscript on star-autonomous hyperdoctrines and predicate linear logic (item 101 here). I’m not sure what the status of this paper is [I haven’t seen it myself], but perhaps that is roughly along the lines of what you are suggesting here. If you see him sometime, you could ask.

Posted by: Todd Trimble on March 5, 2009 2:38 PM | Permalink | Reply to this

Re: New Structures for Physics III

I would feel more liberated if I knew a real use for linear logic.

Speaking for myself, the main benefit I’ve derived from MLL has been on the syntactic side, where I used some key ideas from the theory of Girard’s proof nets to give a solution to the coherence problem for symmetric monoidal closed categories (addressing in particular the difficulties in dealing with the unit). I highly doubt that I would have found this, had I not found about proof nets in the way I did.

This may be a good place to announce that I’ve decided to write up a revised version of my (unpublished) thesis on this topic, which some people have asked about over the years. I hope to have it ready in a few weeks’ time, on my page at the nLab. I’ll let people know when it’s ready.

Posted by: Todd Trimble on March 4, 2009 10:31 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

But $\Pi$ is justified as a categorification of for $\forall$ (again, especially from a perspective of propositions as types), whereas power objects are a new higher-order ingredient.

Okay, fair enough. But I don’t think it’s really fair to complain when higher-order stuff happens to come along for free, just because you weren’t looking for it. If I try to construct the syntactic infinitary-pretopos of an infinitary geometric theory, I end up with a topos, not just an infinitary-pretopos—but that doesn’t make the construction wrong.

Also, while every Boolean $\Pi$ -pretopos is a topos, the most you can say about a Boolean pretopos is that it has a subobject classifier. Consider, for example, the category $\Set_{\aleph_1}$ of at-most-countable sets.

(Irrevelant aside: $Set_{\aleph_1}$ is wonderful; it’s a counterexample to so many things. One thing I love about it is that it has a universal object: a morphism $p:E\to B$ such that every other morphism $Y\to X$ is a pullback of $p$ along a unique map $X\to B$ . It’s perfectly fine to have a set of all sets if you don’t allow any higher-order constructions.)

Posted by: Mike Shulman on March 4, 2009 1:26 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Toby wrote:

Of course, you could switch over to dual-intuitionistic logic…

Thanks for your comments!

In a bigger version of this paper we would discuss intuitionistic linear logic, but while we give some references to that subject, all we really talk about is multiplicative intuitionistic linear logic, meaning the fragment that involves $\wedge$ , $\top$ and $\multimap$ .

Posted by: John Baez on March 2, 2009 6:17 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

Is it too late to give a small list of minor corrections and suggestions?

Posted by: Toby Bartels on March 3, 2009 9:14 AM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

No, it’s never too late. I put the paper on the arXiv yesterday, but then Greg Friedman sent me a long list of typos (below), so I fixed those. If you have more, not on that list, I’d like to see them!

Here are the errors he caught, now fixed on the arXiv version:

Page 6, Definition 2. should be $g: Y \to X$

Page 15, Line -6. Should probably be “a 1-dimensional” not “an 1-dimensional”

Page 15, line -4. “There is also _a_ way…”

Page 25, Line starting “For example…” there is a disagreement among the letters. It should be Y (morphism symbol) Z or the Y on the next line should be an X.

Page 31, third line under second tangle diagram - should the 1 be an I?

Page 33, line -4. “finite-dimensional representation_s_.”

Page 37, line 7. I think the F should be the upside down T to be consistent with your other notation here.

Page 38, the displayed equation after “mirror partner for ‘or’” - there’s an extra comma after X_m

page 40, first sentence after second displayed equation - “in _a_ category”

page 43, text line 3 - “electron” not “electronon”

page 47 - first three displayed equations have extra right parentheses at the ends

page 55 - line 6 of section 4.2 - grammatical error. I suggest removing the “are”

page 56 - definition of Basic types: “There is _an_ arbitrarily…”

page 58. line 1 of section 4.3 - “Ambler describe_d_”

page 58, line 2 of section 4.3 - “can _be_ seen”

page 58, first line of last paragraph - “theories” is repeated

page 59, first line of second paragrap - “_an_ impoverished”

page 59, end of second sentence of second paragraph has two periods.

And one general point - there is some inconsistency about whether to use a period after a displayed expression that ends a sentence. For example, it is done both ways on page 47.

Posted by: John Baez on March 3, 2009 9:22 PM | Permalink | Reply to this

Re: New Structures for Physics III

Just a minor correction: The Rosetta Stone is inscribed with two languages, not three. The demotic and hieroglyphic are two scripts for the same language, Egyptian. The demotic is just the “shorthand” version.

Posted by: Marcel van Oijen on March 19, 2009 11:43 PM | Permalink | Reply to this

Re: New Structures for Physics III

$MathML-enabled post (click for more details).$

This paper suggests some great new directions for expanding the set of analogies discussed in the Rosetta Stone:

Yuri Manin, Renormalization and computation I: motivation and background.

Abstract: The main observable quantities in Quantum Field Theory, correlation functions, are expressed by the celebrated Feynman path integrals which are not well defined mathematical objects.

Perturbation formalism interprets such an integral as a formal series of finite–dimensional but divergent integrals, indexed by Feynman graphs, the list of which is determined by the Lagrangian of the theory. Renormalization is a prescription that allows one to systematically “subtract infinities” from these divergent terms producing an asymptotic series for quantum correlation functions.

On the other hand, graphs treated as “flowcharts” also form a combinatorial skeleton of the abstract computation theory and various operadic formalisms in abstract algebra. In this role of descriptions of various (classes of) computable functions, such as recursive functions, functions computable by a Turing machine with oracles etc., graphs can be used to replace standard formalisms having linguistic flavor, such as Church’s $\lambda$ –calculus and various programming languages. The functions in question are generally not everywhere defined due to potentially infinite loops and/or necessity to search in an infinite haystack for a needle which is not there.

In this paper I argue that such infinities in classical computation theory can be addressed in the same way as Feynman divergences, and that meaningful versions of renormalization in this context can be devised. Connections with quantum computation are also touched upon.

Posted by: John Baez on May 1, 2009 12:28 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

February 27, 2009