Greg Egan wrote:
I seem to have reached a bit of a cul-de-sac on the completely general
question of when, for some -set and some subgroup ,
such that .
I have a lot of catching up to do on this thread, but I just want to say a couple of things.
First, while I’m no expert, this seems like a very hard problem at this extremely high level of generality. Maybe with some work we can find some useful sufficient conditions for such a subset to exist for some . Maybe we can find some necessary conditions. But a complete criterion seems tough unless we pick a particular .
Here’s one way to see why. We’re studying actions of groups on sets. These are analogous to representations of groups on vector spaces. They’re more fundamental, I believe. They’re harder in some ways, easier in others.
The analogue of the ‘direct sum’ of group representations is the ‘disjoint union’ of group actions.
So, the analog of an irreducible representation of on a vector space is a transitive action of on a set .
Every rep of is a sum of irreps (at least if we restrict to finite-dimensional reps of finite groups). Similarly, every -set is a disjoint union of transitive -sets (without any parenthetical fine print).
Your question is about taking an action of on a set and trying to completely understand the resulting action of on the power set . I would state your question this way: given a -set , how can we decompose into a disjoint union of transitive -sets?
(Do you see why this is another way of saying the same thing?)
To see why this question is tough, let’s consider its analogue in the world of group representations.
The analogue of is the exterior algebra , since given any basis of , the subsets of that basis form a basis for .
So, the question you’re asking is like this: given an rep of on , how can we decompose into irreps?
This is a very interesting question, but it’s quite substantial. It can be completely settled for particular groups… but not in any very nice way, I think, for an arbitrary group.
So, I’d glad you plan to tackle some specific groups. But, tackling all groups is not very specific! Any finite group is of this form, for example. So is any compact Lie group. You’ll get much further if you zoom in on something more specific.




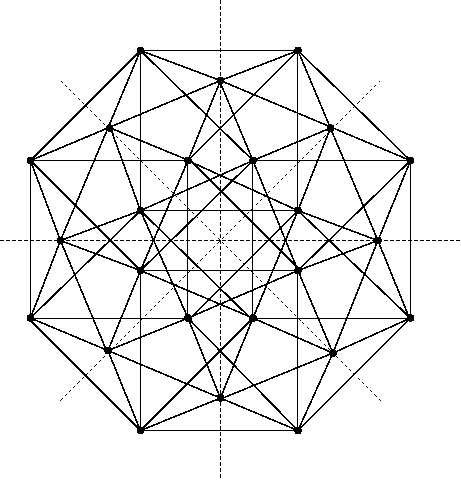
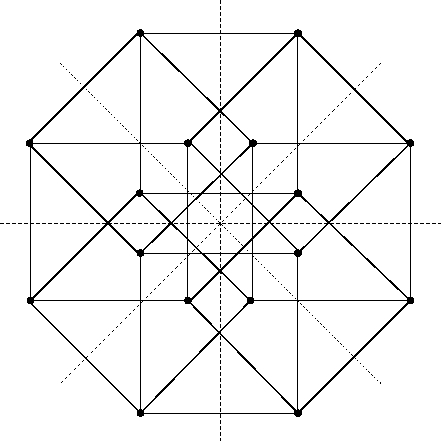
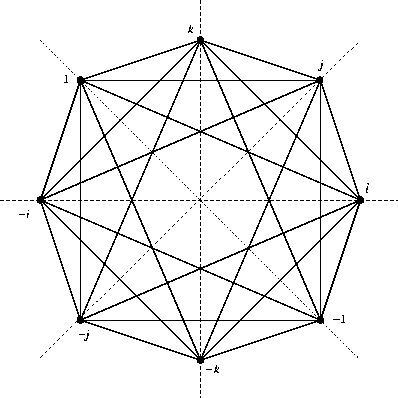


Re: This Week’s Finds in Mathematical Physics (Week 250)
You might emphasize, in the description of the coin-toss game, that you and your friend are required to blurt out your guesses at the same time. Otherwise guesser #1 could say “(My coin is) heads” so guesser #2 is guaranteed to be correct.
Also, a hint for the game: there exists a perfect losing strategy!