Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

June 14, 2008

Computation and the Periodic Table

Posted by John Baez

After visiting Barcelona and Granada, I’m going to this conference:

It will cover diverse subjects including concurrency theory, rewriting systems, computational algebraic topology, visualization and image analysis, distributed computing, and sensor networks. It’s the third of a series; I went to the first in Stanford back in 2001. I don’t see a program for this one yet, but there’s a poster listing some invited speakers.

I just finished making the slides for a talk I’m giving at this conference. Tonight I need to pack. Tomorrow I’ll hop aboard a plane to Spain, and summer will officially begin!

  • John Baez, Computation and the Periodic Table, July 7, 2008.

    Abstract: By now there is an extensive network of interlocking analogies between physics, topology, logic and computer science, which can be seen most easily by comparing the roles that symmetric monoidal closed categories play in each subject. However, symmetric monoidal categories are just the n = 1, k = 3 entry of a hypothesized “periodic table” of kk-tuply monoidal n-categories. This raises the question of how these analogies extend. We present some thoughts on this question, focusing on how monoidal closed 2-categories might let us understand the lambda calculus more deeply. This talk is based on work in progress with Mike Stay.

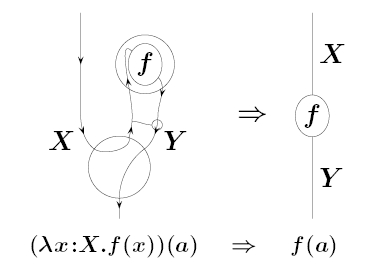
If you know exactly what this picture means, you know the idea I’m trying to explain.

Will I see any of you folks at this conference? I know Eugenia Cheng is, and I imagine Samuel Mimram is too. Anyone else?

Posted at June 14, 2008 12:43 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1714



6 Comments & 1 Trackback

Re: Computation and the Periodic Table

“The 2-morphism analogous to beta-reduction in 2Tang1 is the fold catastrophe”.

Is this fold the same one of catastrophe theory ?

Posted by: Daniel de França MTd2 on June 14, 2008 4:59 AM | Permalink | Reply to this

Re: Computation and the Periodic Table

Yes! For more details see week 18 of the Spring 2007 course notes on Classical vs Quantum Computation. And check out the ‘introduction for experimentalists’ where you can play with a fold and other more subtle catastrophes.

Posted by: John Baez on June 14, 2008 7:34 AM | Permalink | Reply to this

Re: Computation and the Periodic Table

I’ve played with that simulator once you posted before :), and those looked like some kinds of generalized hysteresis graphs, if you followed the stable point, or the movement of a billiard ball in some kind “terrains” with infinite gravitational force.

But I can’t find if there is anything special for the “hysteresis” of every exceptional group.

Also, I found this, it also looks like a periodic table. I mean catastrophe theory is linked to ADE classification which is linked to that tiling and that “McKay correspondence” table. Except that it is flipped.

Posted by: Daniel de França MTd2 on June 14, 2008 6:34 PM | Permalink | Reply to this

Re: Computation and the Periodic Table

Catastrophes got us started on a long conversation a while ago.

Posted by: David Corfield on June 14, 2008 11:14 AM | Permalink | Reply to this

Re: Computation and the Periodic Table

P. 21 should have YYs rather than ZZs.

Posted by: David Corfield on June 14, 2008 12:44 PM | Permalink | Reply to this

Re: Computation and the Periodic Table

Thanks!

Posted by: John Baez on June 14, 2008 6:09 PM | Permalink | Reply to this
Read the post Computation and the Periodic Table II
Weblog: The n-Category Café
Excerpt: I'm giving a talk at LICS 2009 -- this year's annual conference on Logic in Computer Science.
Tracked: August 8, 2009 6:48 PM

Post a New Comment