Klein 2-Geometry X
Posted by David Corfield
Our early work on Klein 2-geometry led us to think about the action of discrete 2-groups. Later we got thinking about actions on vector bundles, seen as categories with abelian vertex groups .
Perhaps the odd thing was why, if we knew we’d need to consider symmetries of groupoids, we never looked more closely at symmetries of a group, i.e., for a group .
One important issue is that doesn’t act transitively on , which takes us away from the Kleinian outlook. On the other hand, we could look at its action on the lattice of subgroups of , where there will be transitive actions on orbits in the lattice. No doubt we ought to be careful, however, categorifying transitivity of action.
We should also think about the lattice of subgroups for powers of . And perhaps also the action of on the category of representations of .
Posted at April 15, 2008 11:23 AM UTC
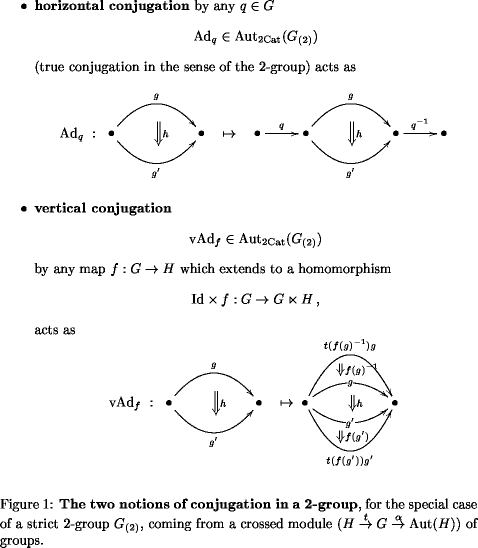
Re: Klein 2-Geometry X