Derek Wise on Cartan Geometry and MacDowell–Mansouri Gravity
Posted by John Baez
I’m mainly here in Paris to talk about categories, logic and games with Paul-André Melliès of the Preuves, Programmes et Systèmes group at Université Paris 7. But, I was invited by Marc Lachièze-Rey of the AstroParticule et Cosmologie group to give a talk on physics.
So, I took this as an excuse to speak about the work of my student Derek Wise.
Derek just finished his thesis in June. This fall he’s going to U. C. Davis. He’s been talking to me about Cartan geometry and MacDowell–Mansouri gravity for several years now — but I’ve been keeping most of it secret, so nobody would scoop his thesis. It’s a great pleasure to finally say more about it!
Abstract and transparencies of the talk follow…
Cartan Geometry and MacDowell-Mansouri Gravity:
the Work of Derek Wise
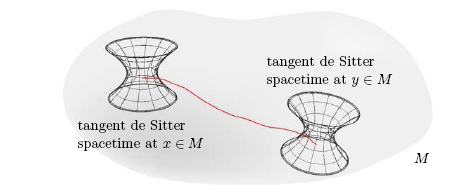
MacDowell and Mansouri invented a clever formulation of general relativity in which the Lorentz connection and coframe field are combined into a single connection with the DeSitter group SO(4,1) or anti-DeSitter group SO(3,2) as gauge group, depending on the sign of the cosmological constant. While this formulation may seem like a ‘trick’, it actually has a deep geometrical meaning. This is best understood in terms of Cartan’s approach to connections — an approach which was somewhat forgotten after his student Ehresmann developed a simpler approach which eventually became standard. Witten’s formulation of 3d gravity as a Chern–Simons theory is also clarified using Cartan geometry. However, in 3 dimensions the relevant Cartan connection is flat and gravity is a topological field theory, while in 4 dimensions this is true only in a certain limit. In this limit, point particles and certain string-like excitations can be nicely described as topological defects. This talk is an exposition of the work of Derek Wise.
Click here to see the slides of the talk:
- Cartan geometry and MacDowell-Mansouri gravity: the work of Derek Wise, in PDF.
Much of this work is contained in Derek’s thesis. While it’s basically done, he’s still polishing it a bit before making it public. For now you can read these papers of his:
- Derek Wise, MacDowell-Mansouri gravity and Cartan geometry.
- John Baez, Alissa Crans and Derek Wise, Exotic statistics for strings in BF theory.
You can also see the transparencies of these talks:
- Derek Wise, Spacetime geometry and Cartan connections, 23rd Pacific Coast Gravity Meeting, Caltech, March 16, 2007.
- Derek Wise, Exotic statistics and particle types in 3d and 4d BF theory, Perimeter Institute, July 13, 2006.
The following papers are very relevant as well:
- Laurent Freidel and Artem Starodubtsev, Quantum gravity in terms of topological observables.
- Laurent Freidel, Jerzy Kowalski-Glikman and Artem Starodubtsev, Particles as Wilson lines of the gravitational field.

Re: Derek Wise on Cartan Geometry and MacDowell–Mansouri Gravity
The url-link of “Quantum gravity in terms of topological observables” needs fixing - remove empty space in paper number.