FFRS on Uniqueness of CFT: Morphisms into Transport Functors
Posted by Urs Schreiber
One of the reformulations of aspects of the FFRS framework which I just mentioned concerns the observation that a solution to the “sewing constraints” of 2d CFT (essentially: “sewing” = “functoriality”) can be regarded as a natural transformation from a trivial TFT functor to a nontrivial one.
By itself, this is just a small cosmetic change, to be explained in detail below.
But it very nicely fits into the general framework of (flat) sections and quantum states as morphisms into transport functors
which I rambled on about various times (first time here, then writing it up more coherently here, and expanding on it here) and which I will talk about (html, pdf) at the Fields Institute workshop.
While for 1-functors this concept tells us little that we don’t already see by inspection, for higher functors it nicely wraps up information that might otherwise be hard to see. For instance, when applied to 2-functors describing parallel transport in line bundle gerbes with connection, this concept of section/quantum state automatically knows that the endpoints of an open string must couple to a D-brane, as described in D-Branes from Tin Cans, II.
(Just in case it is not clear: “tin can diagrams” are those describing the coherence of pseudonatural transformations, hence of morphisms of 2-functors. So D-branes from tin cans alludes precisely to the concept of morphisms into transport 2-functors).
In the FFRS work # only natural transformations into 1-functors
are discussed. But the 1-functor “” here is essentially the 1-functor describing a 3-dimensional topological field theory, and this we expect to be ultimately refined to a 3-functor describing an extended TFT.
In fact, the way I derive the FFRS formalism applied to the disk and the annulus is to write down sections
of a 3-functor with values in 1-dimensional 3-vector spaces as indicated in section 3.4 of From Arrows to Disks.
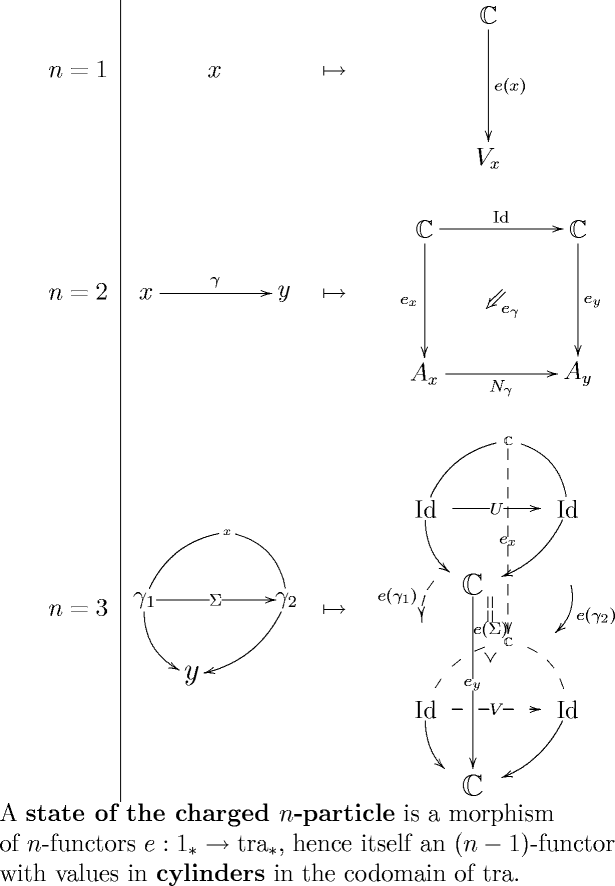
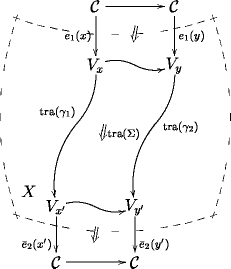
Notice in the last row of this figure how a cylinder with values in , that describes a morphism of 3-functors with values in the 1-dimensional 3-vector space, looks itself already like the crucial piece of data that FFRS postulate has to be associated to a piece of surface: it is an algebra in the surface, in the middle of the cylinder, an object coming from the top of the cylinder, another one, , coming from the bottom, and these all meet in the middle in terms of a morphisms of twisted bimodules
Locally trivializing this and adding suitable incoming and outgoing boundary states
does in fact yield the full FFRS decoration prescription for the disk:
.
It requires some work extracting this, but it is all encoded in a morphism of 3-functors
which is a state of a 3-dimensional extended TFT.
For that reason, I find the reformulation of sewing in the new FFRS work rather interesting. I will describe that in more detail in a followup.