I have thought a little more about the general problem addressed in the above entry. Maybe it is possible to proceed this way:
While it is hard to deal with weak Lie 2-groups, it is easy to deal with weak (i.e. semistrict) Lie 2-algebras. These are nothing but 2-term algebras in a different guise and have a simple list of properties. (See for instance lemma 33 of HDA6 or section 2.2 in our ‘From Loop Groups to 2-Groups’).
So here a Lie 2-algebra element (a morphism in the 2-algebra) is a couple
with and elements of two vector spaces, and the bracket on such couples is
(2)
where
(3)
and
(4)
is the binary operation in the algebra and
(5)
is our 2-term ‘complex’.
Given any such (2-)algebra with a bracket we can try to ‘exponentiate’ it to obtain an algebra we might call as follows:
Let the the elements of be formal symbols
(6)
for each and define the algebra product by means of the Baker-Campbell-Hausdorff formula as
(7)
when is the 2-term algebra of a strict Lie 2-algebra (which then is nothing but a differential crossed module) then is nothing but the algebra under the horizontal product of a strict 2-group (i.e. a crossed module).
More generally we have a non-vanishing Jacobiator
(8)
(for ) and find that the product in is non-associative:
On the one hand we have
(9)
on the other
(10)
Hence there would be an associator
(11)
given to lowest order by
(12)
if we (as necessary to get the associative case right) declare the target of to be
(13)
I haven’t checked if and how this associator extends to all orders.
One more condition I have checked though is the following: Given the above horizontal product, the exchange law in the weak 2-group to-be uniquely specifies the vertical product
of
with . This, however, has to be associative, since it must be just composition of arrows in a category. By working it out one finds that this implies that
(14)
for all .
I am not sure how drastic this restriction cuts down the space of all interesting algebras, though.
Anyway, if we restrict attention to -algebras that do satisfy this the above might be a way to get a handle on weak 2-groups and hence possibly on weakened nonabelian bundle gerbes.
P.S.
For more information on how to use the MathML support of this weblog see this.
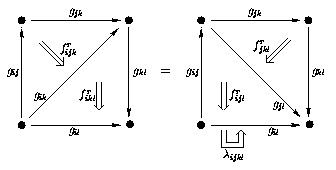
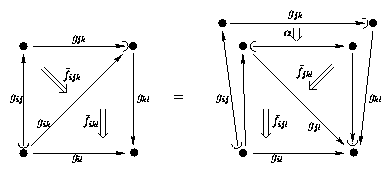

Re: Weak NABG
On a related note, does anyone know where the T_A(h) term in the bitorsor connection pullback equation
l^h* a = Ad_h a + p*T_A(h)
in Aschieri-Cantini-Jurco (hep-th/0312154) comes from? Here l^h is left multiplication by h in our group G, a is the Lie(G)-valued 1-form and A is the Lie(Aut(G))-valued 1-form.
I know it’s related to the a_ij in
A_j + a_ij = gA_ig^{-1} + g^{-1}dg
(with the obvious indices on the g’s), but it seems to be pulled out of the air in the above paper. I know we need it to retain left-right symmetry in the bitorsor but the direction ‘see later’ halfway down page 11 isn’t helpful.
David