Line Bundles on Complex Tori (Part 5)
Posted by John Baez
The Eisenstein integers are the complex numbers of the form where and are integers and . They form a subring of the complex numbers and also a lattice:
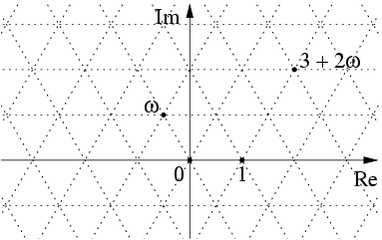
Last time I explained how the space of hermitian matrices is secretly 4-dimensional Minkowski spacetime, while the subset
is 3-dimensional hyperbolic space. Thus, the set of hermitian matrices with Eisenstein integer entries forms a lattice in Minkowski spacetime, and I conjectured that consists exactly of the hexagon centers in the hexagonal tiling honeycomb — a highly symmetrical structure in hyperbolic space, discovered by Coxeter, which looks like this:
Now Greg Egan and I will prove that conjecture.
Last time, based on the work of Johnson and Weiss, we saw that the orientation-preserving symmetries of the hexagonal tiling honeycomb form the group . This is not only as an abstract isomorphism of groups: it’s an isomorphism of groups acting on hyperbolic space, where acts on and its subset by
and this action descends to the quotient .
By general abstract nonsense about Coxeter groups, the orientation-preserving symmetries of the hexagonal tiling honeycomb act transitively on the set of hexagon centers. Thus, if we choose a suitable point , we can get all the hexagon centers by acting on this one. Then the set of hexagon centers is this:
But what’s a suitable point ? I claim that the identity matrix will do, so
Once we show this, we can study the set in detail, allowing us to prove the result conjectured last time:
Theorem. , so the points in the lattice that lie on the hyperboloid are the centers of hexagons in a hexagonal tiling honeycomb.
But first things first: let’s see why the identity matrix can serve as a hexagon center!
The 12 hexagon centers closest to the identity
Suppose we take the identity as a hexagon center and get a bunch of points in hyperbolic space by acting on it by all possible transformations in . We get this set:
But how do we know this is right? We need to check that the points in this set look like the hexagon centers in here:
with the identity smack dab in the middle.
As you can see from the picture, each hexagon center should have 12 nearest neighbors. But does it work that way for our proposed set ? It will be enough to check that the identity matrix has 12 nearest neighbors in , and check that these 12 points are in . A symmetry argument then shows that each point in has 12 nearest neighbors arranged in the same pattern, so the points in are the centers of the hexagons in a hexagonal tiling honeycomb.
It’s easy to measure the distance to the identity matrix if you remember your hyperbolic trig. If we think of as Minkowski spacetime by writing a point as
then the time coordinate is . The distance in hyperbolic space from the identity to a point is then .
But this is a monotonic function of . So let’s find the points with the smallest possible trace — not counting the identity itself, which has trace . We hope there are 12.
Greg Egan found them:
and
where and . These matrices are the 6 magenta points and 6 yellow points shown here, while the black point is the identity:
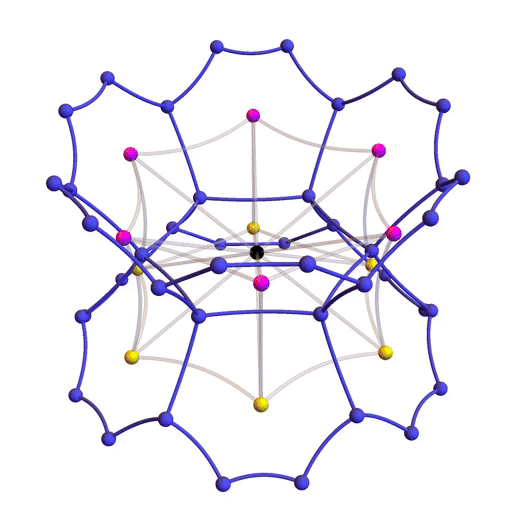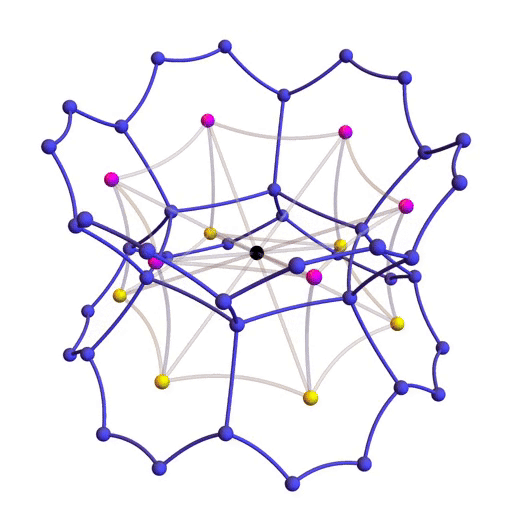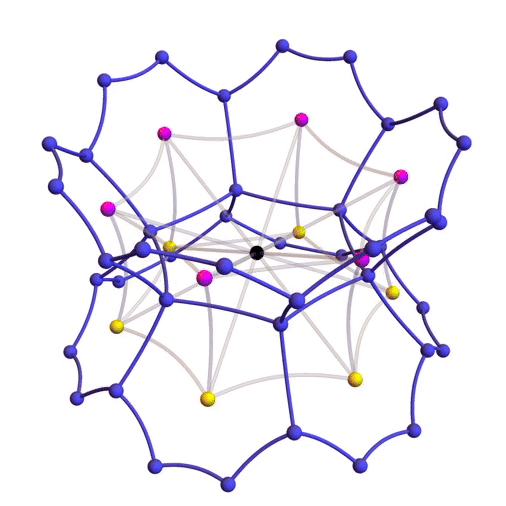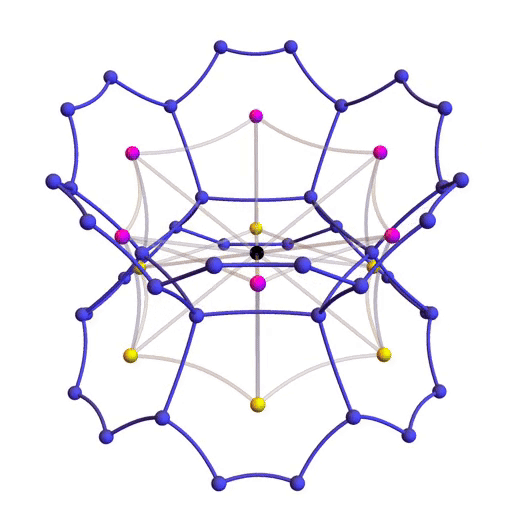
The dark blue points are hexagon vertices, which are not so important right now. By the way, the significance of is that it’s a primitive sixth root of unity; so is . So these give the hexagonal pattern we seek.
These 12 matrices clearly lie in , and they have determinant and positive trace so they lie in . But the good part is this:
Lemma 1. The 12 matrices in equations (1) and (2) are the matrices in that are as close as possible to the identity matrix without being equal to it. In other words, they have the smallest possible trace for matrices in .
I’ll put the proof of this and all the other lemmas in an appendix.
Now, why do these 12 matrices lie in
Greg found 12 matrices that do the job, namely
and
where .
A concrete construction of all the hexagon centers
Now we can get a concrete way to construct every element of the set
Lemma 2. The group consists of finite products of matrices of the form
for .
Lemma 3. Every element of is an element of multiplied on the right by some power of
Notice that this element is in but not in , and it acts on Minkowski space as a 60 degree rotation in the plane, giving the rotational symmetry in Greg’s image:

While we can implement this 60 degree rotation with an element of , namely
we cannot do it with any element of . This is why we need to bring into the game.
Lemma 4. The set equals the set of matrices where is a finite product of matrices of the form
for .
The theorem: first proof
Now we outline two proofs of the conjecture from last time. Greg did the hard part of the first proof, which uses some computer algebra we will only sketch. But the basic idea is this. We want to show that the points in the lattice that lie on the hyperboloid are precisely the centers of the hexagons in our hexagonal tiling honeycomb. It’s easy to show that all the hexagon centers lie in . The hard part is showing the converse. For this we assume we’ve got a point in that’s not a hexagon center. We assume it’s as close as possible to the identity matrix. Then, we’ll find another such point that’s even closer — so no such point could exist.
Theorem. The points in the lattice that lie on the hyperboloid are precisely the centers of hexagons in a hexagonal tiling honeycomb, since
Proof. Part of this theorem is easy. Unfolding the definitions, we need to show
But the only units in the Eisenstein integers are the 6th roots of unity, so for any its determinant is one of those, so and of course . This shows the set on the left-hand side is included in the set on the right-hand side.
So, the hard part is to show the reverse inclusion:
By Lemma 4, it suffices to assume has and , and prove that is of the form , where is a finite product of matrices
for or .
For a contradiction, suppose there exists with and that is not of this form. Since the set of such is discrete, we can choose one with the smallest possible trace. We now find one with a smaller trace, namely either or for some .
We can write
for integers obeying the extra conditions:
If we act on with each of the 12 elements , the changes in the trace of the original matrix are linear expressions in either and or and . It will only be impossible to reduce the trace if all 12 expressions are non-negative, for parameters where the determinant is 1.
It is easier to see what’s happening on a plot:

We would need to find values of and such that the green ellipse (the determinant condition) has a point with integer coordinates inside the smaller of the two hexagons (one of which scales with , the other with ).
The shape of the ellipse and hexagons are such that if the ellipse passed through any one hexagon vertex it would pass through all of them.
We can write the changes in the trace as:
Setting these to zero gives us the sides of the hexagons, while the vertices are found by solving:
to obtain:
The result for is the same, but with replaced by . Substituting these values into the formula for the determinant of and equating that to 1 gives us:
and for :
Without loss of generality we can assume , and use the curve defined by the second equation as the boundary for the region in the parameter space where the determinant ellipse contains points inside the -hexagon. The plot below shows that this only happens for , the identity matrix.
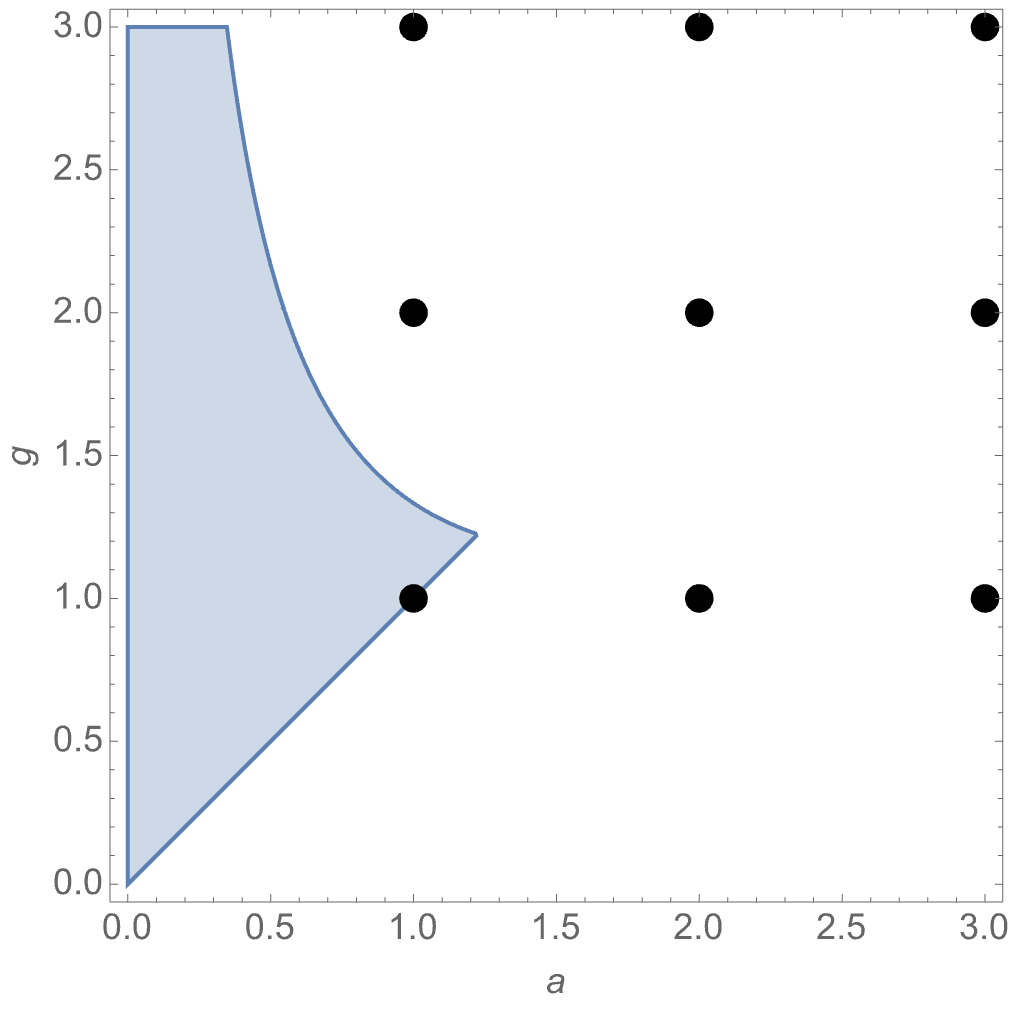
So, unless we are starting with the identity matrix, we can always act with one of the 12 elements and get an element with a smaller positive trace. █
The theorem: second proof
After Greg gave the above proof on Mathstodon, Mist gave a different proof which uses more about Coxeter groups. In this approach, the argument that keeps reducing the trace of a purported counterexample is replaced by the standard fact that every Coxeter group acts transitively on the chambers of its Coxeter complex. I will quote their proof word for word.
Theorem. The points in the lattice that lie on the hyperboloid are precisely the centers of hexagons in a hexagonal tiling honeycomb, since
Proof. Let me start with with elements denoted and equipped with the negative of the Minkowski form, that is, . Inside here, I choose vectors
By checking inner products, we see that these vectors and the aforementioned bilinear form determine a copy of the canonical representation of the rank-4 Coxeter group with diagram
where the 6 means that the edge is labeled ‘6’. My notation for the canonical representation is consistent with that of the Wikipedia article Coxeter complex.
By the general theory, the canonical representation acts transitively on the set of chambers, where the fundamental chamber is the tetrahedral cone cut out by the hyperplanes (through the origin) which are orthogonal to . Direct computation (e.g. matrix inverse) shows us that the extremal rays of the fundamental chamber are given by the vectors
Here I have dropped constant factors, but one can (and perhaps should) normalize to ensure Minkowski norm 1. Now I check explicitly that these vectors match up with Greg’s earlier explicit description of “a portion of the honeycomb”:
- The vector is one of the blue vertices of the hexagon centered on the black point.
- The vector after normalization becomes the midpoint of the two blue vertices indexed by and .
- The vector is the identity matrix, i.e. the black point.
- The vector (1, 0, 0, 1) is the null vector for one of the two horospheres which contains the hexagon centered on the black point.
According to the Wikipedia article Hexagonal tiling honeycomb, the desired honeycomb is constructed from the aforementioned Coxeter group by applying the Wythoff construction with only the first vertex circled. This confirms that the hexagon centers correspond to the vector and its images under the Coxeter group action.
It remains to show that the hexagon centers coincide with the elements of the Eisenstein lattice with Minkowski norm 1.
To show that the hexagon centers are contained in the Eisenstein lattice, it suffices to show that the Eisenstein lattice is invariant under the Coxeter group action. This follows by checking the action of each of the simple reflections:
In more detail, for , the inner product is a half-integer if is in the Eisenstein lattice, and the claim follows because is in the Eisenstein lattice. The same statement applies for and , and ‘half-integer’ can even replaced by ‘integer.’ For , the inner product is an integer multiple of , and the claim follows because is in the Eisenstein lattice.
To show that the elements of the Eisenstein lattice with Minkowski norm are hexagon centers, it suffices to show this statement within the fundamental chamber. Let be the null vector from before. Observe the following: - If lies in the forward light cone, i.e. and , then . - If lies in the Eisenstein lattice, then is an integer. - If lies in the fundamental chamber and satisfies , then . (Sketch: Restricting to gives hyperbolic geometry, and the interior-of-horosphere is convex, so it suffices to check the special cases when is a vertex of the fundamental chamber.) These observations imply that, if is an element of the Eisenstein lattice with lying in the fundamental chamber, then .
Next, write . Since rewrites as , the relation rewrites as . This tells us that the elements of the Eisenstein lattice with and are in bijection with the Eisenstein integers via
It is easy to check that the simple reflections preserve the aforementioned set of vectors and this bijection intertwines those simple reflections with the usual reflection symmetries of the Eisenstein integers (viewed as the vertices of the equilateral triangle lattice). Therefore, all of the aforementioned vectors v can be brought to via a Coxeter group action, as desired. █
What’s next?
A very similar theorem should be true for another regular hyperbolic honeycomb, the square tiling honeycomb:
Here instead of the Eisenstein integers we should use the Gaussian integers, , consisting of all complex numbers with .
Conjecture. The points in the lattice that lie on the hyperboloid are the centers of squares in a square tiling honeycomb.
I’m also very interested in how these results connect to algebraic geometry! That’s the real theme of this series, and I discussed the connection last time. Briefly, the hexagon centers in the hexagonal tiling honeycomb correspond to principal polarizations of the abelian variety . These are concepts that algebraic geometers know and love. Similarly, if the conjecture above is true, the square centers in the square tiling honeycomb will correspond to principal polarizations of the abelian variety . But I’m especially interested in interpreting the other features of these honeycombs — not just the hexagon and square centers — using ideas from algebraic geometry.
Proofs of lemmas
Lemma 1. The 12 matrices
are the points in that as close as possible to the identity matrix without being equal to it. In other words, they have the smallest possible trace for matrices in .
Proof. Matrices in are of the form
where , , the trace is and the determinant is . Since and are integers, and must be integers divided by 2.
The smallest possible trace for such a matrix is , realized only by the identity matrix. We are looking at the second smallest possible trace, which is . So, we have and , i.e. . Since is a half-integer and is an Eisenstein integer, the only options are to let and let be an Eisenstein integer of norm , i.e. a sixth root of unity. These give the matrices
for . █
Lemma 2. The group consists of finite products of matrices of the form
for .
Proof. In Section 8 of Quadratic integers and Coxeter groups, Johnson and Weiss cite Bianchi to say that is generated by these matrices:
The second and third of these matrices equal and , respectively, so we just need to write the first,
as a product of matrices and (or their inverses, which are again matrices of this form). Since
we have
Since the first matrix in this product is , it suffices to note that
is the product of and . █
Lemma 3. Every element of is an element of multiplied on the right by some power of
Proof. The determinant of any is some sixth root of unity, and the determinant of is a primitive sixth root of unity, so for some power we have and thus . It follows that equals some element of , namely , multiplied on the left by some power of , namely . █
Lemma 4. The set equals the set of matrices where is a finite product of the matrices and .
Proof. By Lemma 3, is exactly the set of matrices where and
But the adjoint of is its inverse so
Thus, by Lemma 2, is exactly the set of matrices where is a finite product of the matrices and . █



Re: Line Bundles on Complex Tori (Part 5)
Over on Mastodon, Mist proved the new conjecture!
Conjecture. The points in the lattice that lie on the hyperboloid are the centers of squares in a square tiling honeycomb.
I’ll quote Mist here:
The proof strategy I used before also works for the Gaussian lattice and square tiling honeycomb. Here’s an outline:
Using the same notation as before for hermitian matrices, where the matrix
is viewed as a vector , and using the negative of the Minkowski form, namely , I choose vectors
and check that they have the correct pairwise inner products to be a root system for the Dynkin diagram
o–(4)–o–(4)–o—o
which corresponds to the square tiling honeycomb, as stated here: https://en.wikipedia.org/wiki/Square_tiling_honeycomb
The first vertex of the Dynkin diagram is circled, meaning that the vertices of the squares in the tiling correspond to the extremal ray of the fundamental chamber which lies opposite to the facet defined by . The shape of the fundamental chamber implies that the centers of the squares correspond to the extremal ray of the fundamental chamber which lies opposite to the facet defined by . We can check that this extremal ray points in the direction of , i.e. towards the identity matrix.
To check that the Gaussian lattice is invariant under the simple reflections (and therefore contains the set of square centers), we let v be any element of the Gaussian lattice and consider the reflection
For , the inner product is an integer, and itself belongs to the Gaussian lattice, so the image lies in the Gaussian lattice. For , the inner product is times something in the Gaussian lattice, and the claim follows from the fact that lies in the Gaussian lattice.
To check that every norm-1 element of the Gaussian lattice is a square center, use the same strategy as before. The null vector again is an extremal ray of the fundamental chamber, and one can show that every norm-1 element of the Gaussian lattice which lies in the (closed) fundamental chamber satisfies , i.e. it lies on the horosphere defined by this same equation. Again, this horosphere can be explicitly described as the set of points , and such a point is an element of the Gaussian lattice if and only if and are both integers. We can again check that the reflections generate a group which acts transitively on the 2D lattice of such pairs , so every norm-1 element of the Gaussian lattice is conjugate to , as desired.
Remark: The easiest way to figure out what have to be is to first figure out the points on the horosphere , figure out how the simple reflections for must act on those points, and then look at the difference between each point and its image to find vectors parallel to .