Grothendieck–Galois–Brauer Theory (Part 5)
Posted by John Baez
Lately I’ve been talking about ‘separable commutative algebras’, writing serious articles with actual proofs in them. Now it’s time to relax and reap the rewards! So this time I’ll come out and finally explain the geometrical meaning of separable commutative algebras.
Just so you don’t miss it, I’ll put it in boldface. And in case that’s not good enough, I’ll also say it here! Any commutative algebra gives an affine scheme called its spectrum, and is separable iff can be separated into the diagonal and the rest!
I’ll explain this better in the article.
Let’s try to get a clearer geometrical picture of what I’ve been talking about lately.
The algebra I’ll be discussing today works for any commutative algebra over any commutative ring . And so does the geometry! The idea is to think of as an algebra of functions on some sort of space . Algebraic geometers call this sort of space an affine scheme over , and call the spectrum of . But don’t let that intimidate you! I’ll draw pictures of very simple cases, like where is a line.
Since is the algebra of functions on , is the algebra of functions on . The idea is that given functions and on we get a function on by
Notice, there are two different ways to multiply functions in by functions on . One is on the left:
This multiplies a function on by a function that depends only on ‘ coordinate’:
The other is on the right:
This multiplies a function on by a function that depends only on ‘ coordinate’:
This fact — that you can multiply functions on by functions in in two ways, which obey nice associative laws — can be summarized by saying that is an -bimodule.
By the way, the term ‘ and coordinates’ is a bit poetic here: a better thing to say might be ‘first and second variables’. But when is the real line, my picture of is this:
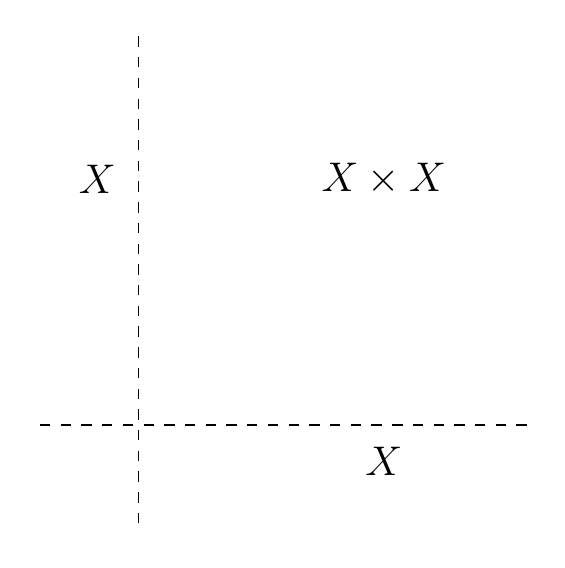
and in this example, and really are just the usual and coordinates.
Now, sitting inside is the diagonal
This plays a starring role in all that follows, so please visualize it:
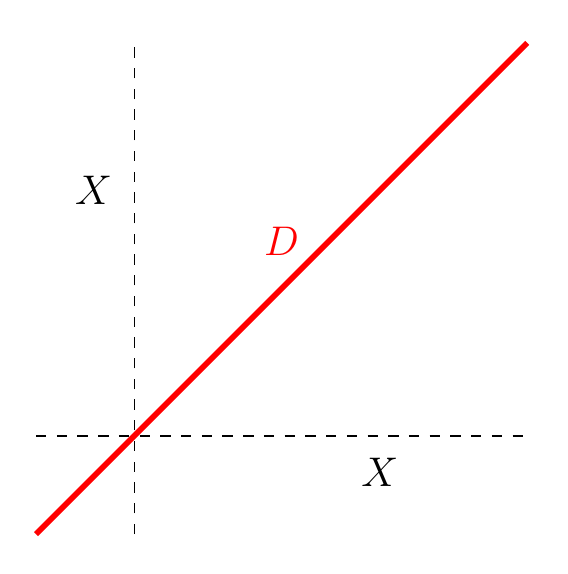
The functions vanishing on the diagonal form an ideal in . Let’s call it . Algebraically, this ideal is precisely the kernel of the multiplication map
I wish this were more visually obvious to me, but it follows from the proof of Lemma 15.
The quotient ring is the ring of functions on the diagonal. But of course, the diagonal is isomorphic to itself. So,
We can dignify this fact by saying we’ve got a short exact sequence of -bimodules:
where is the inclusion of the ideal in . Here is an -bimodule where the left and right actions of agree. That makes sense, since on the diagonal we have .
In Lemma 16 I pointed out something simple but important: the algebra is separable iff this short exact sequence splits! Concretely, this means there’s an -bimodule homomorphism
such that is the identity. This implies the ideal is actually a commutative ring, since taking the unit and applying to it we get a unit for — check it out! So, for a separable algebra we get a way of chopping up like this:
not only as -bimodules, but as commutative rings.
This means we can take the ring of functions on and separate it into two parts that are themselves rings. One of them is , the functions that vanish on the diagonal. The other is , which is the functions that vanish off the diagonal.
And now we finally come to the main point:
The geometrical meaning of separability is that we can separate into two disjoint pieces: the diagonal and the complement .
Yes, the word ‘separable’ actually means you can separate into two pieces. I thank Tom Leinster for pointing this out to me. Finally the word makes sense.
Most commutative algebras are not separable. An affine scheme is not usually the coproduct of the diagonal and ‘the rest’. The problem is that ‘the rest’ snuggles up arbitrarily close to the diagonal.
For example, in the world of affine schemes the plane is not the disjoint union of the diagonal line and the rest of the plane. So the pictures I’ve been showing so far do not illustrate the separable case.
Here’s an example of the separable case:
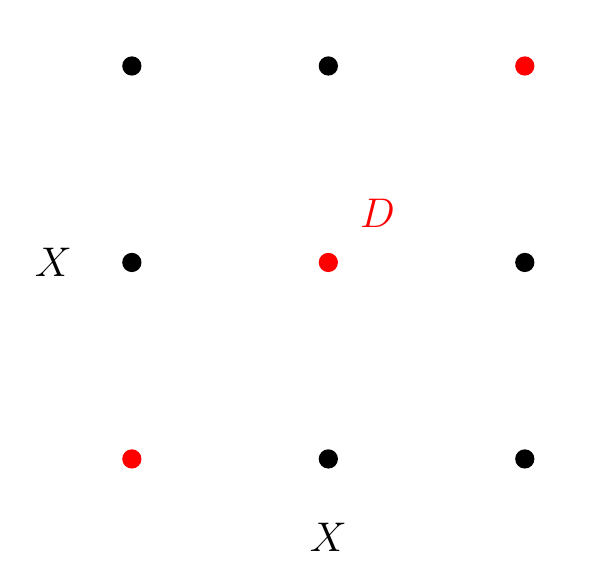
Now is just three points. is all 9 points shown above. The diagonal is the red points, and the ‘rest’, , is the 6 black points. So breaks cleanly into the diagonal and the rest.
All this is related to calculus in a great way. consists of functions on modulo functions that vanish to second order on the diagonal. In our example where is the real line, consists of Taylor series where we expand about the diagonal, like this:
but then throw out all the higher order terms! You see, so , and in we set it to zero. We’re left with a first-order Taylor series of this form:
Since is nonzero in but its square is zero, it acts like an ‘infinitesimal’. This is part of a whole philosophy relating nilpotent elements of rings to infinitesimals.
In general, for any commutative algebra , people call the affine scheme corresponding to is the ‘first-order infinitesimal neighborhood of the diagonal’ in . I visualize it sort of like this:
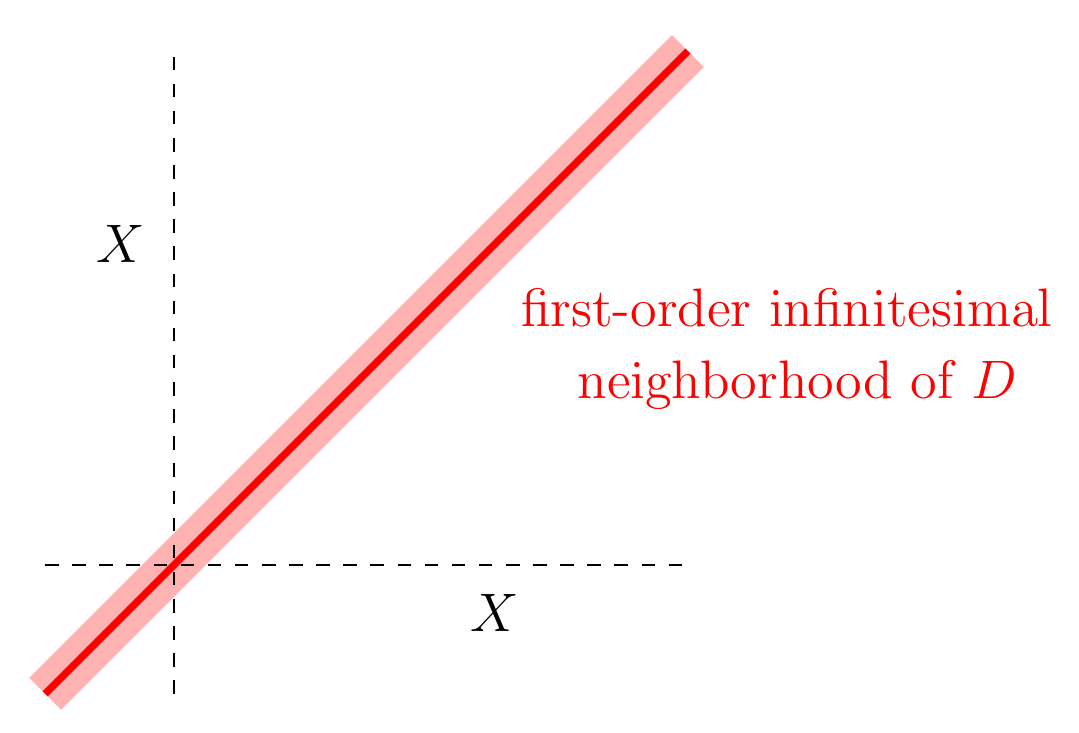
It’s hard to draw accurately, because it’s thicker than a line but only infinitesimally thicker. Algebraic geometers often call this sort of infinitesimal thickening ‘nilpotent fuzz’.
Next, what about ? This consists of functions on that vanish on the diagonal modulo functions that vanish to second order on the diagonal. And these are the same as 1-forms on , since they say to first order how a function changes as you start at a point and then start moving to a nearby point .
But by ‘1-forms’, what I really mean are Kähler differentials, elements of . I defined these in Part 3, and Lemma 15 proved that
So, if what I’m saying now seems annoyingly hand-wavy, check that out.
What happens if is separable? First, the diagonal in is the same as its own first-order infinitesimal neighborhood. There’s nothing ‘infinitesimally close’ to the diagonal except the diagonal itself! This is easy to believe in our example where is a finite set of points:

But it’s also rigorous math: if is separable then the ideal has a multiplicative unit, so , and
Second, if is separable there aren’t any nonzero 1-forms on . More precisely:
This is a precise way of saying that the affine scheme is ‘zero-dimensional’.
So, much of what I’ve been doing has a nice geometrical meaning. Atiyah famously claimed:
Algebra is the offer made by the devil to the mathematician. The devil says: “I will give you this powerful machine, it will answer any question you like. All you need to do is give me your soul: give up geometry and you will have this marvellous machine.”
I don’t agree. To me there is insight to be had in algebra as well as geometry: it’s not just a “powerful machine”. But even if you agree with Atiyah, you can cheat the devil. You can compute using algebra, and then go back and interpret what you’ve done using geometry.
By the way, besides algebra and geometry there’s also logic. The diagonal corresponds to the predicate . If is the spectrum of a separable algebra, there’s also an affine scheme corresponding to the predicate , and a version of the ‘law of excluded middle’ holds.

Re: Grothendieck–Galois–Brauer Theory (Part 5)
This has a nice resonance with the Euler characteristic of a manifold as the self intersection of the manifold with itself in the tangent space. This meshes nicely with the infinitesimal neighborhood of the diagonal. This is an algebraic versions of the fact that the normal bundle of the diagonal is the tangent bundle i think.