Commutative Separable Algebras III
Posted by John Baez
I wrote two blog articles on this theme back in 2010:
Now for rather different reasons I’m returning to it.
A separable algebra over a commutative ring is an algebra that’s projective as -module. That may sound dry, but you can see three other equivalent definitions here. For example, a separable algebra is an algebra that can be given a comultiplication obeying the Frobenius laws:
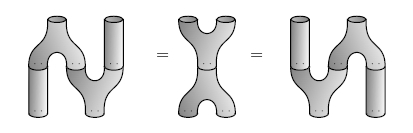
and the special law:
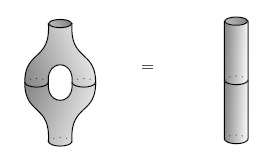
Lately I’ve been trying to understand Azumaya algebras, which are separable algebras over whose center is just . The interesting Azumaya algebras are of course the noncommutative ones, since the only commutative one is itself.
But commutative separable algebras are also interesting. They are important in Grothendieck’s approach to Galois theory. So, I want to understand them better, to better understand how Azumaya algebras are connected to Galois theory.
So, back to commutative separable algebras! And this time we’ll see how they show up in the Fundamental Theorem of Grothendieck Galois Theory!
First let me talk about commutative separable algebras over a field . These are just the finite direct sums of finite-dimensional separable extensions of . If you don’t know what a separable extension is, well for starters every finite-dimensional extension of a finite field, or a field of characteristic zero, is separable. So to a zeroth approximation, you can think of a separable extension as one that’s not really weird.
But in algebraic geometry, we think of commutative algebras as being spaces, with the arrows between them turned around. Then each field corresponds to a ‘kind of point’ , and an extension of that field is a fatter kind of point that maps down to :
Then the basic idea is that is separable if and only if this map doesn’t map any nonzero tangent vectors on to zero tangent vectors down on . (More precisely, this is true when is finite-dimensional over .)
Of course it’s weird to think that one kind of point could map in an interesting way down to another kind of point — or that a point could have nonzero tangent vectors! But this is part of the fun of algebraic geometry.
Anyway, if a field has no finite-dimensional separable extensions except itself, we say it’s separably closed. This happens, for example, if it’s algebraically closed. When this happens, the study of commutative separable algebras over simplifies immensely. In this case the only such algebras are the finite products .
Geometrically speaking, in this case there’s only one kind of point that can sit over our point , namely the same kind of point! Thus, the most general sort of zero-dimensional space that can sit over this point is just a finite collection of points of this kind. The algebra of functions on this finite set is then .
So we get a result:
Theorem. If a field is separably closed, the opposite of the category of commutative separable algebras over is equivalent to .
In the case some related results later became important in relating quantum mechanics to set theory:
- Bob Coecke, Dusko Pavlovic and Jamie Vicary, A new description of orthogonal bases.
but these were formulated in terms of commutative Frobenius algebras rather than commutative separable algebras.
Right now I’m eager to look at fields that aren’t separably closed! Then we get different kinds of point that can sit over the kind of point corresponding to : one for each finite-dimensional separable extension of . And using some ideas from Galois theory, Grothendieck proved this:
The Fundamental Theorem of Grothendieck Galois Theory. The opposite of the category of commutative separable algebras over a field is equivalent to the topos of continuous actions on finite sets of the absolute Galois group of .
The absolute Galois group of is the Galois group of the separable closure of over . We should think of the separable closure as a kind of ‘universal cover’ of the point corresponding to , and the absolute Galois group as a group of ‘deck transformations’ of this cover. (How a point could have an interesting fundamental group is another one of the mysteries of algebraic geometry!) This absolute Galois group naturally gets a structure of a profinite group, so it gets a topology.
Now, while this is fascinating, it’s tempting to generalize. First we could generalize from fields to commutative rings, and look at commutative separable algebras over such rings. Grothendieck did this, I’m pretty sure.
But we could also go further and look at commutative monoids in some sufficiently nice symmetric monoidal category . (When these are just commutative rings.)
One nice thing is that the opposite of the category of commutative monoids in a symmetric monoidal category is always a cartesian category. This exhibits the duality between ‘commutative algebras’ and ‘spaces’ in a very general, simple way.
But we can also define commutative separable monoids in . Many of the different equivalent definitions of commutative separable algebra generalize straightforwardly. And it turns out that Aurelio Carboni generalized the Fundamental Theorem of Grothendieck Galois Theory to commutative separable monoids in any sufficiently nice symmetric monoidal category!
He did it here:
- Aurelio Carboni, Matrices, relations, and group representations.
(A deceptively elementary-sounding title!)
Here is what he proved:
Theorem. Let be a compact closed additive category with coequalizers. Then the opposite of the category of separable commutative monoids in is an essentially small Boolean pretopos.
Even though I’m not advanced enough to find a Boolean pretopos heartwarming, I know it’s a generalization of the category of finite sets. So this is nice. But do any of you have anything more to say about this, like examples of Boolean pretopoi that show up this way, which aren’t topoi?
Someone who likes string diagrams should rewrite large sections of Carboni’s paper using those. There are a lot of intimidating calculations that should become very pretty.
By the way, I heard about Carboni’s theorem here:
- Georgios Chara-Lambous, On the relationship between Galois and Tannakian categories: an open letter.
I found this paper quite fun to read, mainly because it clarified some connections I’ve been trying to make lately.

Re: Commutative Separable Algebras III
For applications of Azumaya algebras to physics, see:
D-branes and Azumaya noncommutative geometry: From Polchinski to Grothendieck
and
Azumaya noncommutative geometry and D-branes - an origin of the master nature of D-branes