The n-Category Café

Last time, we introduced the idea of a “reference measurement”: a measurement that lets us write our quantum states for a system as probability distributions. Mathematically speaking, such a measurement is a positive-operator-valued measure whose elements form a basis for the space of Hermitian operators on a finite-dimensional Hilbert space. Because the elements form a basis, we can represent any Hermitian operator as a list of its inner products with the basis elements. The textbook rules of quantum theory tell us that, if we ascribe the quantum state $\rho$ to our system of interest, then the probability of obtaining the $i$-th outcome of the measurement $\{E _i \}$ is $p(i) = tr(\rho E_i)$. So, if our operators $\{E_i\}$ form a basis, then we can replace the matrix of complex numbers $\rho$ with the vector of nonnegative real numbers $p$. In order to be “informationally complete” like this, a POVM must have at least $d^2$ elements, where $d$ is the dimension of our system’s Hilbert space. We focused our attention on the symmetric informationally complete POVMs, or SICs, which have exactly $d^2$ elements. We defined a SIC as a set of $d^2$ unit vectors $|\pi_j\rangle$ that have pairwise inner products of equal magnitude:

$$|\langle \pi_j | \pi_k \rangle|^2 = \frac{d \delta_{j k} + 1}{d+1}.$$

The projectors onto these lines comprise a POVM when scaled appropriately:

$$E_j = \frac{1}{d} | \pi_j \rangle\langle \pi_j |.$$

Fixing a SIC thus establishes a mapping from the set of quantum states into the ($d^2 - 1)$-dimensional probability simplex. If $\rho$ and $\sigma$ are two quantum states whose probabilistic representations are $p_\rho$ and $p_\sigma$, then the Hilbert–Schmidt inner product of these states is simply related to the Euclidean inner product of the probability vectors:

$$tr(\rho \sigma) = d(d+1)\sum_{i=1}^{d^2} p_\rho(i) p_\sigma(i) - 1.$$

From this, it follows that

$$\frac{1}{d(d+1)} \leq p_\rho \cdot p_\sigma \leq \frac{2}{d(d+1)}.$$

The upper bound is attained if and only if $\rho = \sigma$ and $tr \rho^2 = 1$, which happens when $\rho$ is a “pure state”, i.e., $\rho = | \psi\rangle\langle \psi |$ for some vector $|\psi\rangle$. The set of all quantum states for Hilbert-space dimension $d$ is the convex hull of the pure states. Intriguingly, once we use a SIC to write quantum states as probabilities, then the question of how close a state is to the boundary of state space is a matter of diversity! The effective number of possible outcomes for a SIC measurement given a pure state $p_\psi$ is the pleasingly combinatorial quantity

$$\left( p_\psi \cdot p_\psi \right)^{-1} = \frac{d(d+1)}{2}.$$

Today, we will bring the Weyl group of the $\mathrm{E}_6$ root system into the picture. There will be a slight amount of nomenclatural turbulence, since Hermann Weyl’s name will be associated with two different kinds of group, but that’s just the risk you run in this business.

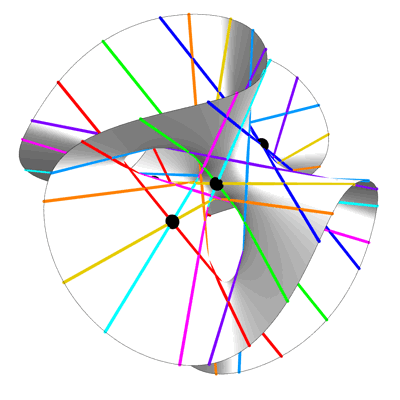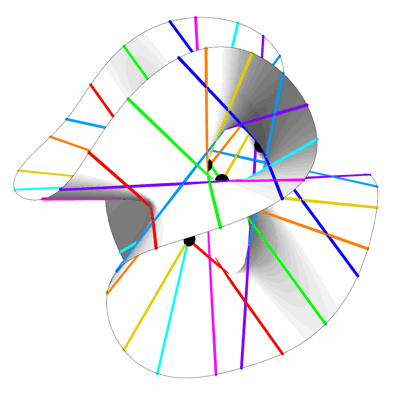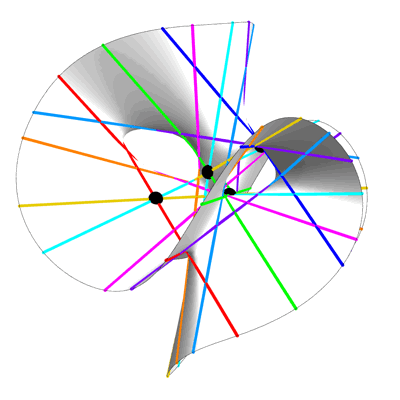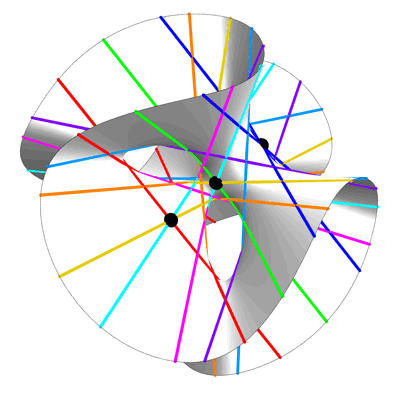
Our primary reference for the next bit will be H. S. M. Coxeter’s Regular Complex Polytopes (Cambridge University Press, 1991). Coxeter devotes a goodly portion of chapter 12 to the Hessian polyhedron, which lives in $\mathbb{C}^3$ and has 27 vertices. These 27 vertices lie on nine diameters in sets of three apiece. (In a real vector space, only two vertices of a convex polyhedron can lie on a diameter. But in a complex vector space, where a diameter is a complex line through the center of the polyhedron, we can have more.) He calls the polyhedron “Hessian” because its nine diameters and twelve planes of symmetry interlock in a particular way. Their incidences reproduce the Hesse configuration, a set of nine points on twelve lines such that four lines pass through each point and three points lie on each line.

Coxeter writes the 27 vertices of the Hessian polyhedron explicitly, in the following way. First, let $\omega$ be a cube root of unity, $\omega = e^{2\pi i / 3}$. Then, construct the complex vectors

$$(0, \omega^\mu, -\omega^\nu),\ (-\omega^\nu, 0, \omega^\mu), \ (\omega^\mu, -\omega^\nu, 0),$$

where $\mu$ and $\nu$ range over the values 0, 1 and 2. As Coxeter notes, we could just as well let $\mu$ and $\nu$ range over 1, 2 and 3. He prefers this latter choice, because it invites a nice notation: We can write the vectors above as

$$0\mu\nu,\ \nu0\mu,\ \mu\nu0.$$

For example,

$$230 = (\omega^2, -1, 0),$$

and

$$103 = (-\omega, 0, 1).$$

Coxeter then points out that this notation was first introduced by Beniamino Segre, “as a notation for the 27 lines on a general cubic surface in complex projective 3-space. In that notation, two of the lines intersect if their symbols agree in just one place, but two of the lines are skew if their symbols agree in two places or nowhere.” Consequently, the 27 vertices of the Hessian polyhedron correspond to the 27 lines on a cubic surface “in such a way that two of the lines are intersecting or skew according as the corresponding vertices are non-adjacent or adjacent.”

Casting the Hessian polyhedron into the real space $\mathbb{R}^6$, we obtain the polytope known as $2_{21}$, which is related to $\mathrm{E}_6$, since the Coxeter group of $2_{21}$ is the Weyl group of $\mathrm{E}_6$. The Weyl group of $\mathrm{E}_6$ can also be thought of as the automorphism group of the 27 lines on a cubic surface.

We make the connection to symmetric quantum measurements by following the trick that Coxeter uses in his Eq. (12.39). We transition from the space $\mathbb{C}^3$ to the complex projective plane by collecting the 27 vertices into equivalence classes, which we can write in homogeneous coordinates as follows:

$$\begin{array}{ccc} (0, 1, -1), & (-1, 0, 1), & (1, -1, 0) \\ (0, 1, -\omega), & (-\omega, 0, 1), & (1, -\omega, 0) \\ (0, 1, -\omega^2), & (-\omega^2, 0, 1), & (1, -\omega^2, 0) \end{array}$$

Let $u$ and $v$ be any two of these vectors. We find that

$$|\langle u, u\rangle|^2 = 4$$

when the vectors coincide, and

$$|\langle u, v\rangle|^2 = 1$$

when $u$ and $v$ are distinct. We can normalize these vectors to be quantum states on a three-dimensional Hilbert space by dividing each vector by $\sqrt{2}$.

We have found a SIC for $d = 3$. When properly normalized, Coxeter’s vectors furnish a set of $d^2 = 9$ pure quantum states, such that the magnitude squared of the inner product between any two distinct states is $1/(d+1) = 1/4$.

Every known SIC has a group covariance property. Talking in terms of projectors, a SIC is a set of $d^2$ rank-1 projectors $\{\Pi_j\}$ on a $d$-dimensional Hilbert space that satisfy the Hilbert–Schmidt inner product condition

$$tr (\Pi_j \Pi_k) = \frac{d\delta_{j k} + 1}{d+1}.$$

These form a POVM if we rescale them by $1/d$. In every known case, we can compute all the projectors $\{\Pi_j\}$ by starting with one projector, call it $\Pi_0$, and then taking the orbit of $\Pi_0$ under the action of some group. The projector $\Pi_0$ is known as the fiducial state. (I don’t know who picked the word “fiducial”; I think it was something Carl Caves decided on, way back.)

In all known cases but one, the group is the Weyl–Heisenberg group in dimension $d$. (Don’t worry, octonion fans! We’ll be getting to the exception soon.) To define this group, fix an orthonormal basis $\{|n\rangle\}$ and define the operators $X$ and $Z$ such that

$$X|n\rangle = |n+1\rangle,$$

interpreting addition modulo $d$, and

$$Z|n\rangle = e^{2\pi i n / d} |n\rangle.$$

The Weyl–Heisenberg displacement operators are

$$D_{l\alpha} = (-e^{i\pi / d})^{l\alpha} X^l Z^\alpha.$$

Because the product of two displacement operators is another displacement operator, up to a phase factor, we can make them into a group by inventing group elements that are displacement operators multiplied by phase factors. This group has Weyl’s name attached to it, because he invented $X$ and $Z$ back in 1925, while trying to figure out what the analogue of the canonical commutation relation would be for quantum mechanics on finite-dimensional Hilbert spaces. It is also called the generalized Pauli group, because $X$ and $Z$ generalize the Pauli matrices $\sigma_x$ and $\sigma_z$ to higher dimensions (at the expense of no longer being Hermitian).

To relate this with the Coxeter construction we discussed earlier, turn the first of Coxeter’s vectors into a column vector:

$$\left(\begin{array}{r} 0 \\ 1 \\ -1\end{array}\right).$$

Apply the $X$ operator twice in succession to get the other two vectors in Coxeter’s table (converted to column-vector format). Then, apply $Z$ twice in succession to recover the right-hand column of Coxeter’s table. Finally, apply $X$ to these vectors again to effect cyclic shifts and fill out the table. This set of nine vectors is known as the Hesse SIC.

Each of the 27 lines corresponds to a weight in the minimal representation of $\mathrm{E}_6$, and so each element in the Hesse SIC corresponds to three weights of $\mathrm{E}_6$.

In dimension $d = 3$, we encounter a veritable cat’s cradle of vectors. First, there’s the Hesse SIC. Like all informationally complete POVMs, it defines a probabilistic representation of quantum state space, in this case mapping from $3 \times 3$ density matrices to the probability simplex for 9-outcome experiments. As we did last time for the qubit case, we can look for the pure states whose probabilistic representations minimize the Shannon entropy. The result is a set of twelve states, which sort themselves into four orthonormal bases of three states apiece. What’s more, these bases are mutually unbiased: The Hilbert–Schmidt inner product of a state from one basis with any state from another is always constant. In a sense, the Hesse SIC has a “dual” structure, and that dual is a set of Mutually Unbiased Bases (MUB). This duality relation is rather intricate: Each of the 9 SIC states is orthogonal to exactly 4 of the MUB states, and each of the MUB states is orthogonal to exactly 3 SIC states.

An easy way to remember these relationships is to consider the Hesse configuration that we mentioned earlier. This configuration is also known as the discrete affine plane on nine points, and as the Steiner triple system of order 3. That’s a lot of different names for something which is pretty easy to put together! To construct it, first draw a $3 \times 3$ grid of points, and label them consecutively:

$$\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}$$

These will be the points of our discrete geometry. To obtain the lines, we read along the horizontals, the verticals and the leftward and rightward diagonals:

$$\begin{array}{ccc} (123) & (456) & (789) \\ (147) & (258) & (369) \\ (159) & (267) & (348) \\ (168) & (249) & (357) \end{array}$$

Each point lies on four lines, and every two lines intersect in exactly one point. For our purposes today, each of the points corresponds to a SIC vector, and each of the lines correponds to a MUB vector, with point-line incidence implying orthogonality. The four bases are the four ways of carving up the plane into parallel lines (horizontals, verticals, diagonals and other diagonals).

To construct a MUB vector, pick one of the 12 lines we constructed above, and insert zeroes into those slots of a 9-entry probability distribution, filling in the rest uniformly. For example, picking the line $(123)$, we construct the probability distribution

$$\left(0,0,0,\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6} \right).$$

This represents a pure quantum state that is orthogonal to the quantum state

$$\left(\frac{1}{6},\frac{1}{6},\frac{1}{6},0,0,0,\frac{1}{6},\frac{1}{6},\frac{1}{6} \right)$$

and to

$$\left(\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{6},0,0,0 \right),$$

while all three of these have the same Hilbert–Schmidt inner product with the quantum state represented by

$$\left(0,\frac{1}{6},\frac{1}{6},0,\frac{1}{6},\frac{1}{6},0,\frac{1}{6},\frac{1}{6} \right),$$

for example.

Considering all the lines in the original structure that are orthogonal to a given line in the dual yields a maximal set of real equiangular lines in one fewer dimensions. (Oddly, I noticed this happening up in dimension 8 before I thought to check in dimension 3, but we’ll get to that soon.) To visualize the step from $\mathbb{C}^3$ to $\mathbb{R}^2$, we can use the Bloch sphere representation for two-dimensional quantum state space. Pick a state in the dual structure, i.e., one of the twelve MUB vectors. All the SIC vectors that are orthogonal to it must crowd into a 2-dimensional subspace. In other words, they all fit into a qubit-sized state space, and we can draw them on the Bloch sphere. When we do so, they are coplanar and lie at equal intervals around a great circle, a configuration sometimes called a trine. This configuration is a maximal equiangular set of lines in the plane $\mathbb{R}^2$.

What happens if, starting with the Hesse SIC, you instead consider all the lines in the dual structure that are orthogonal to a given vector in the original? This yields a SIC in dimension 2. I don’t know where in the literature that is written, but if feels like something Coxeter would have known.

All of this ends up being significant for quantum computation and for a no-go theorem about hidden variables, but right now, the pertinent point is how the study of exceptional Lie groups is starting to enter our tale of quantum measurements.

And we’ve barely scratched the surface! Here’s something else to ponder. Let’s consider the stabilizer group of the Hesse fiducial. That is, let’s take the vector

$$\frac{1}{\sqrt{2}} \left(\begin{array}{r} 0 \\ 1 \\ -1 \end{array}\right)$$

and consider those unitary operations which hold it fixed while permuting the other 8 vectors in the Hesse SIC among themselves. This is a subgroup of the symmetry group of the Hesse SIC, and it is known to be isomorphic to $SL(2, \mathbb{F}_3)$, the group of unit-determinant $2 \times 2$ matrices over the three-element finite field. But this group has other names, too: It is isomorphic to the binary tetrahedral group, which we get by taking the vertices of the 24-cell and multiplying them together as quaternions.

Another path from the sporadic SICs to $\mathrm{E}_6$ starts with the qubit SICs, i.e., regular tetrahedra inscribed in the Bloch sphere. Shrinking a tetrahedron, pulling its vertices closer to the origin, yields a type of quantum measurement (sometimes designated a SIM) that has more intrinsic noise. Apparently, $\mathrm{E}_6$ is part of the story of what happens when the noise level becomes maximal and the four outcomes of the measurement merge into a single degenerate case. This corresponds to a singularity in the space of all rotated and scaled tetrahedra centered at the origin. Resolving this singularity turns out to involve the Dynkin diagram of $\mathrm{E}_6$: We invent a smooth manifold that maps to the space of tetrahedra, by a mapping that is one-to-one and onto everywhere except the origin. The pre-image of the origin in this smooth manifold is a set of six spheres, and two spheres intersect if and only if the corresponding vertices in the Dynkin diagram are connected.

This observation prompted this series of blog posts, but I’m still not sure how it’s connected to the other things we’re exploring!