The Involute of a Cubical Parabola
Posted by John Baez
In his remarkable book The Theory of Singularities and its Applications, Vladimir Arnol’d claims that the symmetry group of the icosahedron is secretly lurking in the problem of finding the shortest path from one point in the plane to another while avoiding some obstacles that have smooth boundaries.
Arnol’d nicely expresses the awe mathematicians feel when they discover a phenomenon like this:
Thus the propagation of waves, on a 2-manifold with boundary, is controlled by an icosahedron hidden at an inflection point at the boundary. This icosahedron is hidden, and it is difficult to find it even if its existence is known.
I would like to understand this!
I think the easiest way for me to make progress is to solve this problem posed by Arnol’d:
Puzzle. Prove that the generic involute of a cubical parabola has a cusp of order 5/2 on the straight line tangent to the parabola at the inflection point.
There’s a lot of jargon here! Let me try to demystify it. (I don’t have the energy now to say how the symmetry group of the icosahedron gets into the picture, but it’s connected to the ‘5’ in the cusp of order 5/2.)
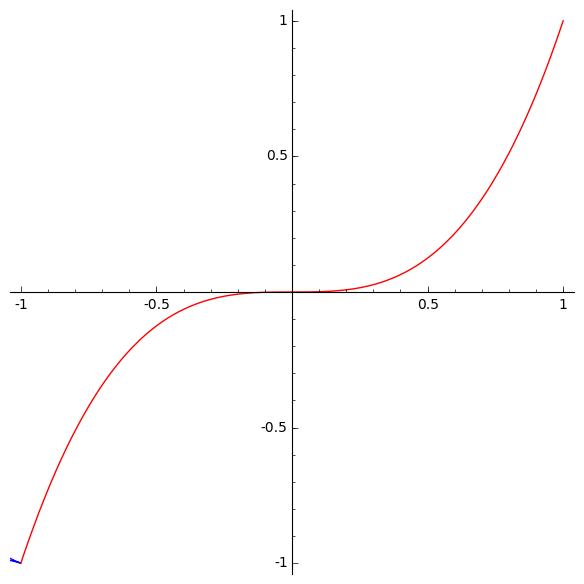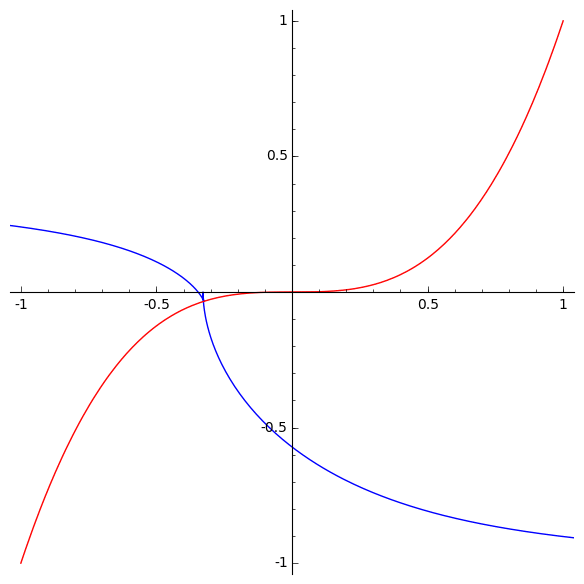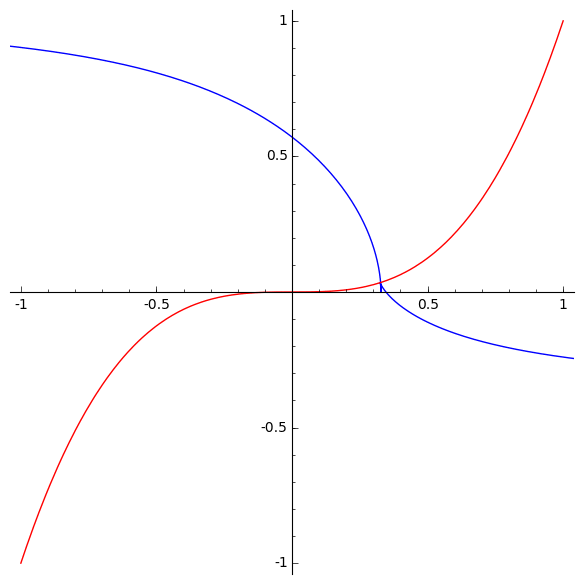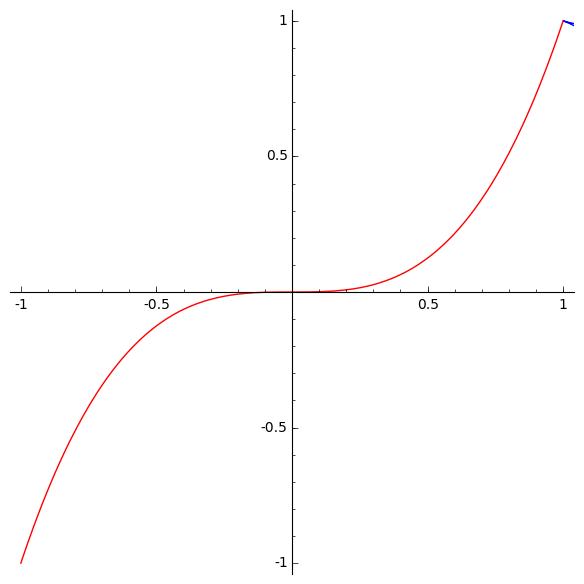
A cubical parabola is just a curve like :
It’s a silly name. I guess looked at and said “I want to be a parabola too!”
The involute of a curve is what you get by attaching one end of a taut string to that curve and tracing the path of the string’s free end as you wind the string onto that curve. For example:
Here our original curve, in blue, is a catenary: the curve formed by a hanging chain. Its involute is shown in red.
There are a couple of confusing things about this picture if you’re just starting to learn about involutes. First, Sam Derbyshire, who made this picture, cleverly moved the end of the string attached to the catenary at the instant the other end hit the catenary! That allowed him to continue the involute past the moment it hits the catenary. The result is a famous curve called a tractrix.
Second, it seems that the end of the string attached to the catenary is ‘at infinity’, very far up.
But you don’t need to play either of these tricks if you’re trying to draw an involute. Take a point on a curve . Take a string of length , nail down one end at , and wind the string along . Then the free end of your string traces out a curve .
is called an involute of . It consists of all the points you can get to from by a path of length that doesn’t cross .
So, Arnol’d’s puzzle concerns the involute of the curve .
He wants you to nail down one end of the string at any ‘generic’ location. So, don’t nail it down at , since that point is different from all the rest. That point is an inflection point, where the curve switches from curving down to curving up!
He wants you to wind the string along the curve , forming an involute. And he wants you to see what the involute does when it crosses the line .
This is a bit tricky, since the region is not convex. If you nail your string down at , your string will have to start out above the curve . But when the free end of your string crosses the line , the story changes. Now your string will need to go below the curve .
It’s a bit hard to explain this both simply and accurately, but if you imagine drawing the involute with a piece of string, I think you’ll encounter the issue I’m talking about. I hope I understand it correctly!
Anyway, suppose you succeed in drawing the involute. What should you see?
Arnol’d says the involute should have a ‘cusp of order 5/2’ somewhere on the line .
A cusp of order 5/2 is a singularity in an otherwise smooth curve that looks like in some coordinates. In a recent post I described various kinds of cusps, and in a comment I mentioned that the cusp of order 5/2 was called a rhamphoid cusp. Strangely, I wrote all that before knowing that Arnol’d places great significance on the cusp of order 5/2 in the involute of a cubical parabola!
Simon Burton drew some nice cusps of order 5/2. The curve looks like this:
This is a more typical curve with a cusp of order 5/2:
It looks like this:
It’s not as symmetrical as the curve , but Arnol’d emphasizes that you should usually expect this sort of shape:
It is easy to recognize this curve in experimental data, since after a generic diffeomorphism the curve consists of two branches that have equal curvatures at the common point, and hence are convex from the same side [….]
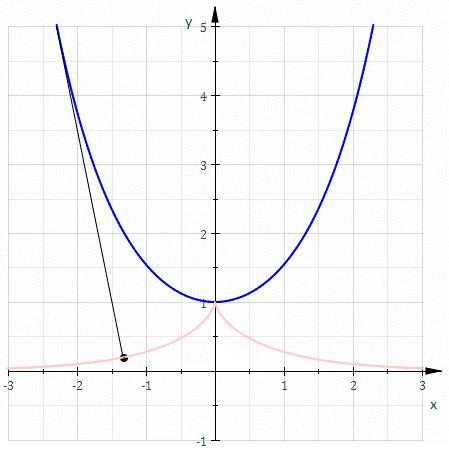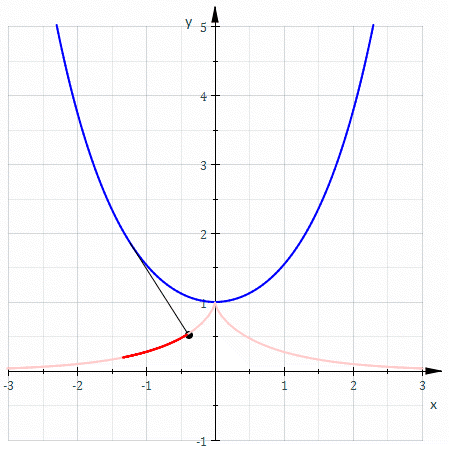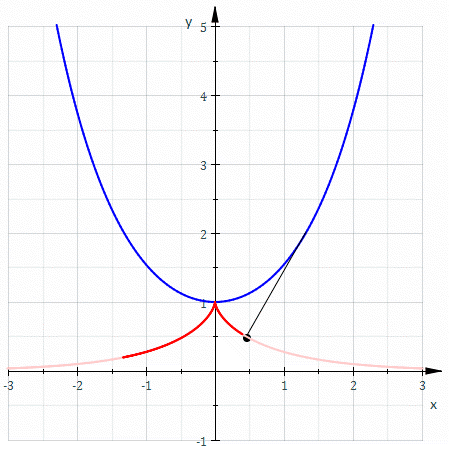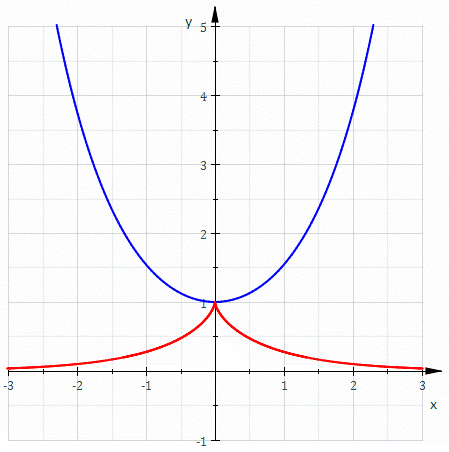
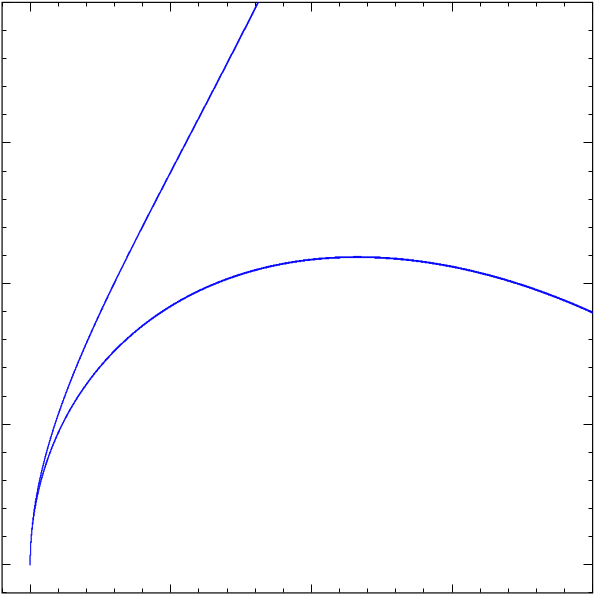
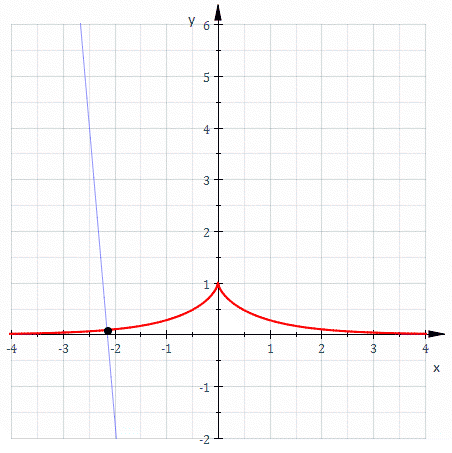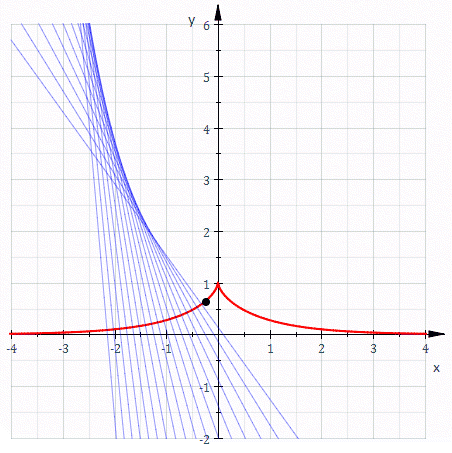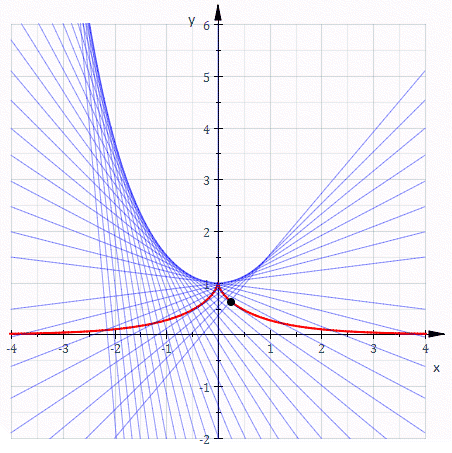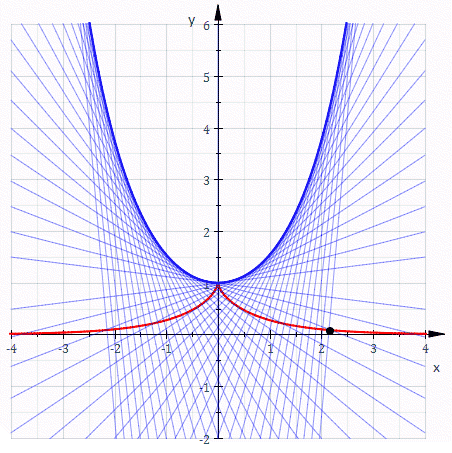
So, if we draw the involutes of a cubical parabola we should see something like this! And indeed, Marshall Hampton has made a great online program that draws these involutes. Here’s one:
The blue curve is the involute. It looks like it has a cusp of order 5/2 where it hits the line It also has a less pointy cusp where it hits the red curve Like the cusp in the tractrix, this should be a cusp of order 3/2, also known as an ordinary cusp.
Hints
Regarding the easier puzzle I posed above, Arnol’d gives this hint:
HINT. The curvature centers of both branches of the involute, which meet at the point of the inflectional tangent, lie at the inflection point, hence both branches have the same convexity (they are both concave from the side of the inflection point of the boundary).
That’s not what I’d call crystal clear! However, I now understand what he means by the two ‘branches’ of the involute. They come from how you need to change the rules of the game as the free end of your string crosses the line . Remember, I wrote:
If you nail your string down at , your string will have to start out above the curve . But when the free end of your string crosses the line , the story changes. Now your string will need to go below the curve .
When the rules of the game change, he claims there’s a cusp of order 5/2 in the involute.
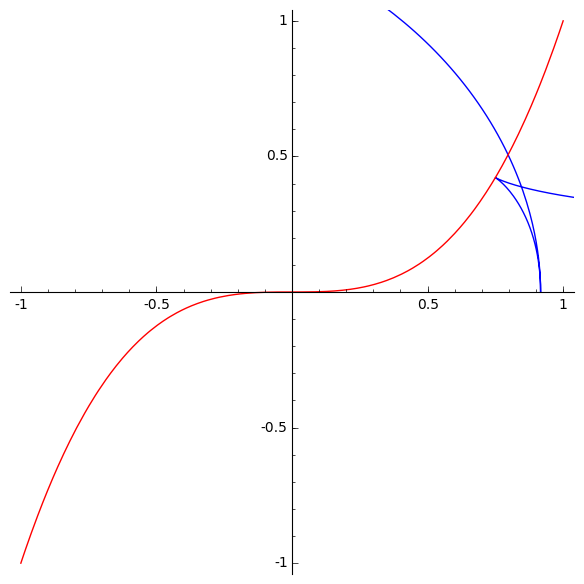
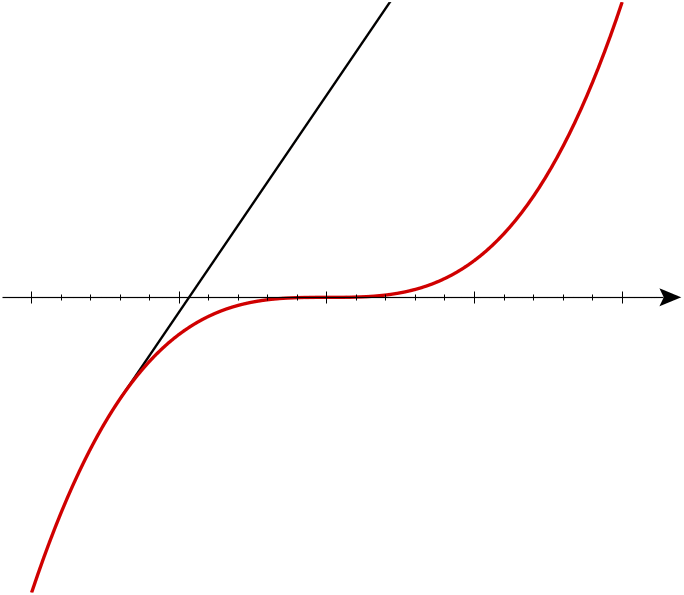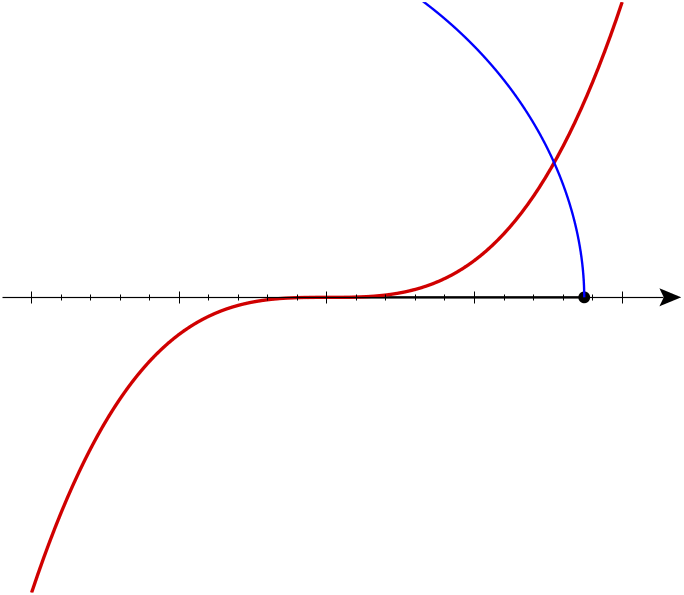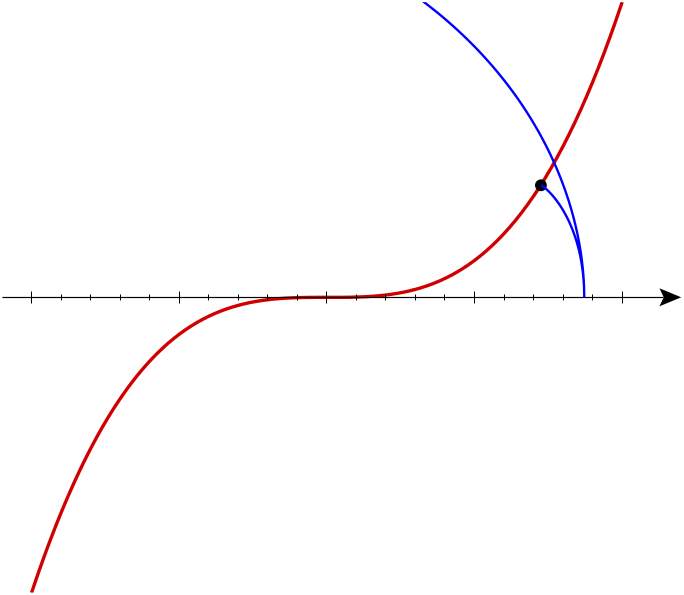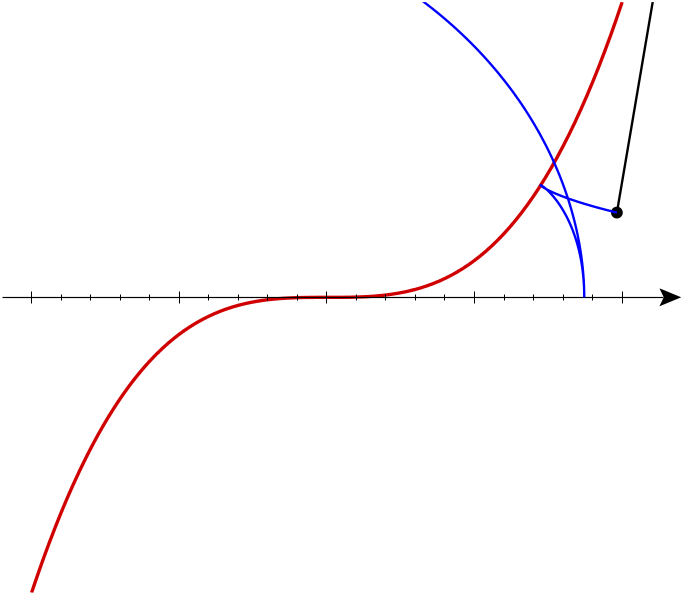
I also think I finally understand the picture that Arnol’d uses to explain what’s going on:
It shows the curve in bold, and three involutes of this curve. One involute is not generic: it goes through the special point . The other two are. They each have a cusp of order 5/2 where they hit the line , but also a cusp of order 3/2 where they hit the curve . We can recognize the cusps of order 5/2, if we look carefully, by the fact that both branches are convex on the same side.
But again, the challenge is to prove that these involutes have cusps of order 5/2 where they hit the line . A cusp of order 7/2 would also have two branches that are convex on the same side!
Here’s one more hint. Wikipedia says that if we have a curve
parametrized by arclength, so
for all , then its involute is the curve
given by
Strictly speaking, this must be an involute. And it must somehow handle the funny situations I described, where the involute fails to be smooth. I don’t know it does this.







Re: The Involute of a Cubical Parabola
The equation is easy to understand. Imagine a string of infinite length lying on top of the curve . Cut it at a point . For each real number , go a distance along the curve (in one direction for and the other for ) to a point we’ll call , and straighten the string between and the point you go to. Align the straightened string with the tangent . Its endpoint will be .
Now is a smooth function. How does that match the singularities shown? Well, just slows down as you approach those singular points. The image of a smooth curve isn’t necessarily smooth…