Morton and Vicary on the Categorified Heisenberg Algebra
Posted by John Baez
Wow! It’s here!
- Jeffrey Morton and Jamie Vicary, The Categorified Heisenberg Algebra I: A Combinatorial Representation.
Back when I was working with Jeffrey Morton on categorifying the harmonic oscillator, I discovered to my surprise that there was another guy, a student of Chris Isham named Jamie Vicary, who was also categorifying the harmonic oscillator, using different but related ideas. Luckily, they started to collaborate… and they discovered some quite wonderful things.
In quantum mechanics, position times momentum does not equal momentum times position! This sounds weird, but it’s connected to a very simple fact. Suppose you have a box with some balls in it, and you have the magical ability to create and annihilate balls. Then there’s one more way to create a ball and then annihilate one, than to annihilate one and then create one.
Huh? Yes: if there are, say, 3 balls in the box to start with, there are 4 balls you can choose to annihilate after you’ve created one but only 3 before you create one.
In quantum mechanics, when you’re studying the harmonic oscillator, it’s good to think about operators that create and annhilate… not balls, but ‘quanta of energy’. The creation operator is called and the annihilation operator is called , and the argument I just sketched can be used to show that
It’s a wonderful fact that you can express the position and momentum of the oscillator in terms of these creation and annihilation operators:
So the fact that position and momentum don’t commute, but instead obey
(in units where Planck’s constant is 1) can be seen as coming from the more intuitive fact that the annihilation and creation operators don’t commute, but instead obey
This insight, that funny facts about quantum mechanics are related to simple facts about balls in boxes, allows us to ‘categorify’ a chunk of quantum mechanics—including the Heisenberg algebra, which is the algebra generated by the position and momentum operators. Now is not the time to explain what that means. The important thing is that Mikhail Khovanov figured out a seemingly quite different way to categorify the same chunk of quantum mechanics, so there was a big puzzle about how his approach relates to the one I just described. Jeffrey Morton and Jamie Vicary have solved that puzzle.
The big spinoff is this. Khovanov’s approach showed that in categorified quantum mechanics, a bunch of new equations are true! These equations are ‘higher analogues’ of Heisenberg’s famous formula
So, these new equations should be important! But they look very mysterious at first:
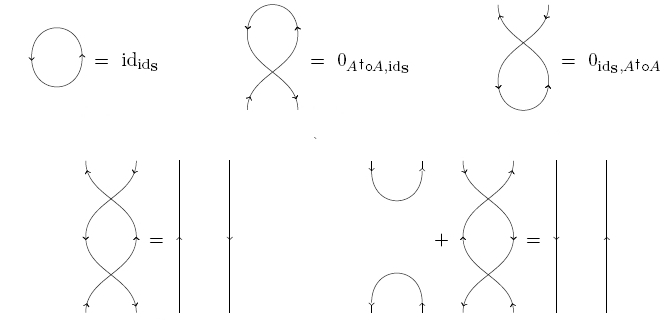
In fact, when I first saw them, it seemed as if Khovanov had just plucked them randomly from thin air! Of course he had not: they arose from the representation theory of symmetric groups. But their intuitive meaning was far from transparent.
Now Jeffrey and Jamie have shown how to get these equations just by thinking about balls in boxes. The equations in fact make perfect sense! See Section 2.8: Combinatorial Interpretation for details. Let me just get you started. We should replace the equation
by an isomorphism
This provides a one-to-one correspondence between ‘ways to annihilate a ball and then create one… together with one more thing’ and ‘ways to create a ball and then annihilate it’. This isomorphism is built from two parts:
and
The thing I’m calling
says how every way to annihilate a ball (say the ball ) and then create a different one (say ) gives a way to create one (namely ) and then annihilate one (namely ). The thing I’m calling
says how there is one other way to create a ball and then annihilate one: namely, by annihilating the same ball we just created!
The five equations shown in the picture above are then a clever graphical way of describing basic facts about the morphisms and and two others which are a bit subtler to describe. These others, which deserve to be called
and
do not give functions that send one way to do things to another. Instead, they give relations. You can’t ‘turn around’ a function and get a function going the other way unless it’s invertible. But you can turn around a function and get a relation going the other way.
I’ve hit the limit on what I can explain without getting more serious and ruining the light-hearted, easy-going tone of this post. If you want details, I’d rather just let you read the paper!
But I’d like to say a few fancier things, just for the experts. In reality, what matters most for Jeffrey and Jamie are not sets and relations, but groupoids and spans of groupoids. Spans of groupoids allow you to ‘turn around’ a functor between groupoids. In our old work on categorifying quantum mechanics, Jeffrey and I used the bicategory of
- groupoids,
- spans of groupoids,
- isomorphism classes of maps of spans of groupoids.
Recently Alex Hoffnung has shown this is a monoidal bicategory—in fact part of a monoidal tricategory if you don’t wimp out and take isomorphism classes at the 2-morphism level, as I just did. (Alex, to his credit, did not.) Mike Stay has gone further and shown it’s a compact closed symmetric monoidal bicategory.
As I said, spans of groupoids let you ‘turn around’ a functor between groupoids, like and get something going the other way, which we denote with a dagger:
This is how we construct the annihilation operator starting from the creation operator in categorified quantum mechanics. But to define 2-morphisms like and above, Jeffrey and Jamie need to turn around maps of spans of groupoids. And to do this, we need spans of spans of groupoids. So they need a monoidal bicategory like this:
- groupoids,
- spans of groupoids,
- isomorphism classes of spans of spans of groupoids.
They show that the equations in Khovanov’s categorified Heisenberg algebra follow from equations between 2-morphisms here… which have nice combinatorial interpretations in terms of balls in boxes!
It would be interesting to see what happens if we go even further. We don’t really need to stop at spans of spans. We could keep on going forever, as noted in the famous Monte Python song:
span, span, span, span…
If we went one notch further we could categorify our categorified Heisenberg algebra and get a 2-categorified Heisenberg algebra. We would find that the equations relating and became isomorphisms, and we could work out what equations those isomorphisms and their daggers satisfy!
The important thing is this: those equations are not something we get to choose, or make up. They are what they are, and they’re just sitting there waiting for us to discover them.
It could be that these higher equations are trivial for some reason. That would be interesting: it would mean that Khovanov’s categorified Heisenberg algebra is the end of the story, not the tip of an even deeper iceberg. Or, maybe these equations are nontrivial! That would be even more interesting!
Of course, there’s also a lot to think about without categorifying further. What if any physical meaning do the relations in the categorified Heisenberg algebra have? Can we actually do something like physics with some categorified version of quantum theory? Or is this stuff mainly good for understanding the representation of symmetric groups in a deeper way, using combinatorics? That would already be very interesting. And so on…

Re: Morton and Vicary on the Categorified Heisenberg Algebra
One comment I’d like to add is that what we have here is, as our title implies, a combinatorial “representation” of Khovanov’s categorification. That is, we have a functor from the monoidal category whose morphisms are those diagrams (which we think of as a 2-category with one object) into the 2-category , where the one object is taken to the groupoid of finite sets and bijections.
Since the morphisms of aren’t functors or maps, it’s not exactly what people often mean by a “categorified representation”, which would be an action on a category in terms of functors and natural transformations. We do talk about how to get one of these on a 2-vector space out of our groupoidal representation toward the end.
So in some sense, Khovanov’s category of diagrams is a universal theory of what a categorification of the Heisenberg algebra must look like, and the combinatorial representation is a particular model of that theory. It’s one which happens to have a nice combinatorial story in which the relations John quoted are easy to see.