The Three-Fold Way (Part 4)
Posted by John Baez
It’s been more than a month since the last post in this thread… so let me remind you of the story so far.
I showed you how real and quaternionic quantum mechanics are lurking inside good old, ordinary complex quantum mechanics. Ordinary physicists only like complex Hilbert spaces. For example, they describe elementary particles using irreducible unitary representations of groups. And these are representations on complex Hilbert spaces. They couldn’t care less about real or quaternionic Hilbert spaces.
But — lo and behold! — the math gods have decreed that irreducible unitary representations come in three kinds:
- The real ones. These are the ones that you get by complexifying representations on real Hilbert spaces. These guys are isomorphic to their own dual. In fact, any representation of this kind comes with an invariant nondegenerate bilinear function with
- The quaternionic ones. These are the ones that you get by taking representations on quaternionic Hilbert spaces, and thinking of them as complex Hilbert spaces. These guys are also isomorphic to their own dual. In fact, any representation of this kind comes with an invariant nondegenerate bilinear map with
- The truly complex ones. These are the ones that aren’t isomorphic to their own dual.
So, even if we don’t want to think about real and quaternionic Hilbert spaces, the math gods are hinting that we should!
And indeed, I showed you that an electron is a quaternion.
Well, that’s just a deliberately overdramatic way of putting it. More precisely, I showed you that any irreducible unitary representation of SU(2) is either real or quaternionic. And the famous ‘spin-1/2’ representation, which we use to describe electrons, is quaternionic. We usually describe the state of a spin-1/2 particle using two complex numbers. But we could also use a single quaternion!
Now, you might think this is a completely trivial statement, since you can take two complex numbers and combine them into one quaternion. That’s part of the idea — but what I’m saying is not quite that trivial. What I’m saying is that acts as quaternion-linear transformations that preserve the inner product on a 1-dimensional quaternionic Hilbert space — and that’s the spin-1/2 representation in disguise.
In fact all the half-integer-spin or ‘fermionic’ representations of SU(2) are quaternionic, while all its integer-spin or ‘bosonic’ representations are real.
I also showed you that a unitary group representation is quaternionic if and only if it comes equipped with an antiunitary operator that commutes with all the group operations and obeys That’s not surprising: this operator is just multiplication by the quaternion . But the cool part is that a unitary group representation is real if and only if it has a with all the same properties, except now Now this operator comes from complex conjugation!
What’s the physical meaning of this operator ? For representations of , it’s time reversal: it reverses the angular momentum!
Okay, now you’re caught up.
Last time I ended with a puzzle:
It seems natural that time reversal should obey , as it does in the bosonic. It may seem strange to have , as we do for fermions. Should not applying time reversal twice get us back where we started? It actually does, in a crucial sense: the expectation values of all observables are unchanged when we multiply a state by . So, time reversing an electron twice gets us an electron that’s physically indistinguishable from the one we started with. Still, the minus sign seems a bit curious.
But it should remind you of the equally curious minus sign that a fermion picks when you rotate it a full turn!
Are these signs related?
The answer appears to be yes, though the following argument is more murky than I’d like. It has its origins in Feynman’s 1986 Dirac Memorial Lecture on antiparticles, together with the well-known ‘belt trick’ for demonstrating that isn’t simply connected — which is why we need its double cover to describe rotations in quantum theory. The argument uses string diagrams, which are a generalization of Feynman diagrams.
The basic ideas apply to any Lie group . If an irreducible unitary representation of this group is isomorphic to its dual, it comes with an invariant nondegenerate pairing We can draw this as a ‘cup’:
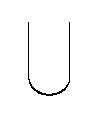
If this were a Feynman diagram, it would depict two particles of type coming in on top and nothing going out at the bottom: since is isomorphic to its dual, particles of this type act like their own antiparticles, so they can annihilate each other.
Since defines an isomorphism , one can show there’s a linear map back from to , which we draw as a ‘cap’:
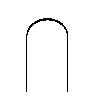
uniquely determined by requiring that the cap and cup obey the zig-zag identities:
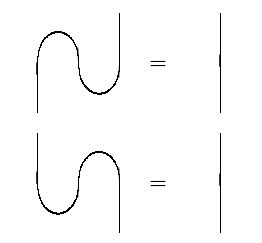
Indeed, for any , we have a ‘cup’ and ‘cap’ obeying the zig-zag equations: in the language of category theory, we say that is compact closed. But when is isomorphic to its dual, we can write the cap and cup using just .
As we have seen, there are are two choices. If is real, obeys Using string diagrams, we can draw this equation as:
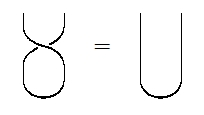
But if is quaternionic, we have which we can draw as:

The power of string diagrams is that we can apply the same diagrammatic manipulation to both sides of an equation and get a new equation. Take the pictures I just drew, turn them clockwise a bit and stretch out the string a little! Then when is a real representation we get:
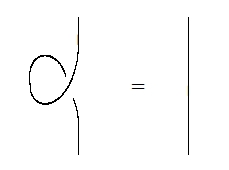
while when is quaternionic we get:
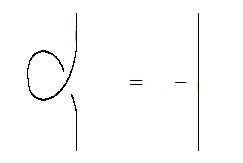
Both sides of these equations describe operators from to itself. The vertical straight line at right corresponds to the identity operator If you do the math, the more complicated diagram at left turns out to correspond to the operator . So, it follows that when the representation is real, while when is quaternionic. Of course I already told you this… but now I’m sketching a picture proof.
While it may seem puzzling to those who have not been initiated into the mysteries of string diagrams, everything so far is perfectly rigorous. Now comes the slightly murky part! The string diagram at left:
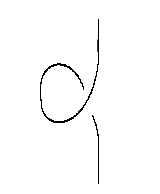
looks like a particle turning back in time, going backwards for a while, and then turning yet again and continuing forwards in time. In other words, it looks like a picture of the square of time reversal! So, the fact that the corresponding morphism is indeed the square of time reversal when somehow seems right.
Moreover, in the theory of string diagrams it is often useful to draw the strings as ‘ribbons’. This allows us to take the diagram at left and pull it tight, as follows:

At left we have a particle (or actually a small piece of string) turning around in time, while at right we have a particle making a full turn in space as time passes. So, in the case it seems to make sense that when the spin is an integer: after all, the state vector of an integer-spin particle is unchanged when we rotate that particle a full turn. Similarly, it seems to make sense that when is a half-integer: the state vector of a half-integer-spin particle gets multiplied by when we rotate it by a full turn.
So, we seem to be on the brink of having a ‘picture proof’ that the square of time reversal must match the result of turning a particle 360 degrees! Unfortunately this argument is not yet rigorous, since we have not explained how the topology of ribbon diagrams (well-known in category theory) is connected to the geometry of rotations and time reversal. We started out talking about group representations… but somehow spacetime snuck into our argument. Can you explain what’s going on?
While our discussion here focused on the group , real and quaternionic representations of other groups are also important in physics. For example, gauge bosons live in the adjoint representation of a compact Lie group on the complexification of its own Lie algebra; since the Lie algebra is real, this is always a real representation of . This is related to the fact that gauge bosons are their own antiparticles.
In the Standard Model, fermions are not their own antiparticles, but in some theories they can be. Among other things, this involves the question of whether the relevant spinor representations of the groups are complex, real (‘Majorana spinors’) or quaternionic (‘pseudo-Majorana spinors’). The options are well-understood, and follow a nice pattern depending on the dimension and signature of spacetime modulo 8. We should emphasize that the spin groups are not compact unless or , so their finite-dimensional complex representations are hardly ever unitary, and many of the results I’ve been explaining don’t apply. Nonetheless, we may ask if such a representation is the complexification of a real one, or the underlying complex representation of a quaternionic one—and the answers have implications for physics.
is not the only compact Lie group with the property that all its irreducible unitary representations on complex Hilbert spaces are real or quaternionic! For a group to have this property, it is necessary and sufficient that every element be conjugate to its inverse. All compact simple Lie groups have this property except those of type for , with odd, and . I learned this from the nice people over on Mathoverflow. And for the symmetric groups , the orthogonal groups , and the special orthogonal groups , all representations are in fact real.
So there is a rich supply of real and quaternionic group representations, which leave their indelible mark on physics even if we think we are doing complex quantum theory!
Next time I want to say more about how real, complex and quaternionic quantum theory fit together. I’ve made it sound like complex quantum theory is the main thing, with the real and quaternionic theories sitting inside it. But that’s just part of the story. To see the whole story, we should use a bit more category theory.



Re: The Three-Fold Way (Part 4)
As usual, when I blog about something I think about it harder and later notice errors in what I said. Usually I correct them but this time I’ll leave it as a puzzle, at least for now.
What mathematical mistake did I make above? I’m not talking about poetic exaggerations like “an electron is a quaternion” — I’m talking about a straightforward mathematical statement that happens to be false.