State-Observable Duality (Part 1)
Posted by John Baez
I’m writing a paper called “Division algebras and quantum theory”, which is mainly about how quantum theory can be formulated using either the real numbers , the complex numbers , or the quaternions — and how these three versions are not really separate alternatives (as people often seem to think), but rather three parts of a unified structure.
This is supposed to resolve the old puzzle about why Nature picked when it was time for quantum mechanics, while turning up her nose at and . The answer is that she didn’t: she greedily chose all three!
But sitting inside this paper there’s a smaller story about Jordan algebras and the Koecher–Vinberg classification of convex homogeneous self-dual cones. A lot of this story is ‘well-known’, in the peculiar sense that mathematicians use this term, meaning at least ten people think it’s old hat. But it’s still worth telling — and there’s also something slightly less well-known, the concept of state-observable duality, which is sufficiently lofty and philosophical as to deserve consideration on this blog, I hope.
So I’ll tell this story here, in three parts. The first is just a little warmup about normed division algebras. If you’re a faithful reader of This Week’s Finds, you know this stuff. The second is also a warmup, of a slightly more esoteric sort: it’s about an old paper on the foundations of quantum theory written by Jordan, von Neumann and Wigner. And the third will be about the Koecher–Vinberg classification and state-observable duality.
The laws of algebra constrain the possibilities for theories that closely resemble the quantum mechanics we know and love. Various classification theorems delimit the possibilities. Of course, theorems have hypotheses. It is easy to get around these theorems by weakening our criteria for what counts as a theory ‘closely resembling’ quantum mechanics; if we do this, we can find a large number of alternative theories. This is especially clear in the category-theoretic framework, where many theories based on convex sets of states give rise to categories of physical systems and processes sharing some features of standard quantum mechanics Here, however, I want to focus on results that pick out real, complex and quaternionic quantum mechanics as special. But before we start, let’s make sure we’re up to speed on our normed division algebras!
After discovering that complex numbers could be viewed as simply pairs of real numbers, Hamilton sought an algebra of ‘triples’ where addition, subtraction, multiplication and division obeyed most of the same rules. Alas, what he was seeking did not exist. After much struggle, he discovered the ‘quaternions’: an algebra consisting of expressions of the form (), equipped with the associative product with unit uniquely characterized by these equations: He carved these equations into a bridge as soon he discovered them:
Yes, that’s him. And he spent the rest of his life working on the quaternions, so this algebra is now called in his honor.
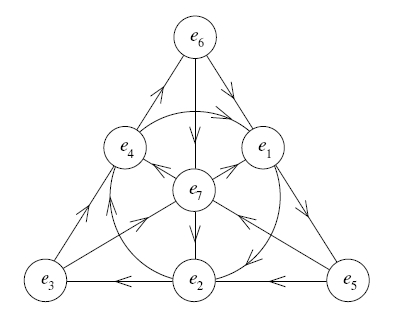
The day after Hamilton discovered the quaternions, he sent a letter describing them to his college friend John Graves. A few months later Graves invented yet another algebra, now called the ‘octonions’ and denoted . The octonions are expressions of the form with . The multiplication of octonions is not associative, but it is still easily described using the Fano plane, a projective plane with 7 points and 7 lines:
This is my feeble attempt to rival Tim Silverman when it comes to pretty pictures. The ‘lines’ here are the sides of the triangle, its altitudes, and the circle containing the midpoints of the sides. Each line contains three points, and each of these triples has a cyclic ordering, as shown by the arrows. If and are cyclically ordered in this way then Together with these rules:
- is the multiplicative identity,
- are square roots of -1,
the Fano plane completely describes the algebra structure of the octonions. If you haven’t done it before, make sure to use these rules to check that the octonions are nonassociative! When is it true that and when is it false? There’s a cute answer.
What is so great about the number systems discovered by Hamilton and Graves? Like the real and complex numbers, they are ‘normed division algebras’. For us, an algebra will be a real vector space equipped with a multiplication that is real-linear in each argument. We do not assume our algebras are associative. We say an algebra is unital if there exists an element with for all . And we define a normed division algebra to be a unital algebra equipped with a norm obeying the rule
The real and complex numbers are obviously normed division algebras. For the quaternions we can define the norm to be: A similar formula works for the octonions: With some sweat, one can check that these rules make and into normed division algebras.
The marvelous fact is that there are no more! In an 1898 paper, Hurwitz proved that , , and are the only finite-dimensional normed division algebras. In 1960, Urbanik and Wright removed the finite-dimensionality condition:
Theorem: Every normed division algebra is isomorphic to either , , or .
For quantum mechanics, it is important that every normed division algebra is a -algebra, meaning it is equipped with a real-linear map obeying these rules: For this map is just complex conjugation, while for it is the identity map. For the quaternions it is given by: and for the octonions, One can check in all four cases we have
For the three associative normed division algebras, the -algebra structure lets us set up a theory of Hilbert spaces. Let’s quickly sketch how. Suppose is an associative normed division algebra. Then we define a -vector space to be a right -module: that is, an abelian group equipped with a map that obeys the laws We say a map between -vector spaces is -linear if for all and . When no confusion can arise, I’ll call a -linear map a linear operator or simply an operator.
Yeah, I know: you’re probably appalled that I’m multiplying by scalars on the right here. It makes no difference except for the quaternions, which are noncommutative. Even in that case, we could use either left or right multiplication by scalars, as long as we stick to one convention. But since we write the operator on the left in the expression , it makes more sense to do scalar multiplication on the right, so no symbols trade places in the law . This will be especially nice when we write the operator using a matrix.
There is a category of -vector spaces and operators between them. As usual, every vector space has a basis, and any two bases have the same cardinality, so we can talk about the dimension of a vector space over , and every finite-dimensional vector space over is isomorphic to . Every operator can be written as matrix: See? This obeys , with the scalar coming out on the right!
The -algebra structure of the normed division algebras becomes important when we study Hilbert spaces. We define an inner product on a -vector space to be a map sending a pair of vectors to a number that is -linear in the second argument: obeys and is positive definite: with equality only for .
As usual, an inner product gives a norm: and we say a -vector space with inner product is a -Hilbert space if this norm makes the vector space into a complete metric space. Every finite-dimensional -Hilbert space is isomorphic to with its standard inner product And, it turns out we can do quantum theory using these Hilbert spaces for either the real numbers, the complex numbers or the quaternions! Next time I’ll tell you a theorem about why these three choices are special.
This is fine for , and : what about ? It would be nice if we could think of as an -dimensional octonionic vector space, with scalar multiplication defined in the obvious way. Unfortunately, the law fails, because the octonions are nonassociative. Furthermore, there are no maps obeying except the zero map. So, nobody has managed to develop a good theory of octonionic linear algebra. (But that doesn’t mean it doesn’t exist!)
While the octonions are nonassociative, they are still ‘alternative’. You’ve heard of people leading an ‘alternative lifestyle’, and that’s very much what the octonions are like. We say an algebra is alternative if the associative law holds whenever two of the elements being multiplied are equal: Surprisingly, this is enough to let us carry out a bit of quantum theory as if , and were well-defined octonionic Hilbert spaces. The 3-dimensional case is by far the most exciting: it leads to a structure called the ‘exceptional Jordan algebra’. This leads to a whole world of fun. But beyond dimension 3, it seems there is little to say.



Re: State-Observable Duality (Part 1)
If you relax the axioms a little further (skip alternativity but keep power associativity), you get sedenions.