Pictures of Modular Curves (V)
Posted by Guest
guest post by Tim Silverman
Welcome back!
Last time, I introduced the subgroup of consisting of what I called the “affine transformations” of , of the form , which preserve the relation “having the same denominator”; and I also introduced two of its subgroups, the “translations”, of the form , which preserve denominators, and the “rescalings” of the form —between them, these two groups generate the affine transformations.
And I said that I intended to talk more about the latter group first. So that is what I am going to do.
The Rescaling Action
We’ll start with the orbits of the action.
Since we’ve decided to organise the tiling by denominator, the first thing to look at is the action on denominators, ignoring numerators. But the action on denominators just amounts to the action of the units in on the elements of by multiplication.
The orbits of the latter action are quite simple to enumerate: they correspond to the factors of . The units themselves form one orbit (corresponding to , since they are all multiples of by a unit). The singleton set is a second orbit (corresponding to , seeing as how mod ). Any other factor of gives its own orbit, consisting of multiples of that factor by units. If and are two different factors of , neither of which is a factor of the other, then there is no way that multiplying one of them by a unit can give a multiple of the other, so the different factors stay separate under the action of multiplication by units. Similarly, if , then multiples of which are not multiples of will still be so after multiplication by any unit.
So, to sum up, each factor of gives rise to an orbit consisting of multiples of which are not multiples of any larger factor of .
Let’s see how this works in a few cases.
We’ll start small, but not too small. For , the group of units is trivial, so not very illustrative for our case. For , the group of units is , or in other words, , but since we are quotienting everything out by , this also reduces to triviality; and the same is true for .
So the first interesting case is . Here the group of units is , and after quotienting out by , we get a group isomorphic to (the group) , for which we can choose representative members . Or, within , we can choose matrices to implement the corresponding rescalings, such as and .
At the same time, we can see that, geometrically, once we start organising things around the “at infinity” faces, whose fractions have denominator , the icosahedron divides into two isomorphic parts (coloured here blue and green):
N = 5: two isomorphic pieces
Consider the action of on the blue fractions:
Viz: the blue fractions are sent to the green fractions.
On the green fractions, the action is of course precisely the reverse. Putting these actions together, this “rescaling” is just a rotation of the sphere through about an axis passing through the equator (with the axis lying roughly in the plane of the page in these particular pictures):
N = 5: action of unit 2
Or side by side for comparison:
N = 5: Before and After
has a group of units consisting of just , hence trivial, so we’ll move onto the more interesting case .
Let’s look once more at the example coloured by denominator.
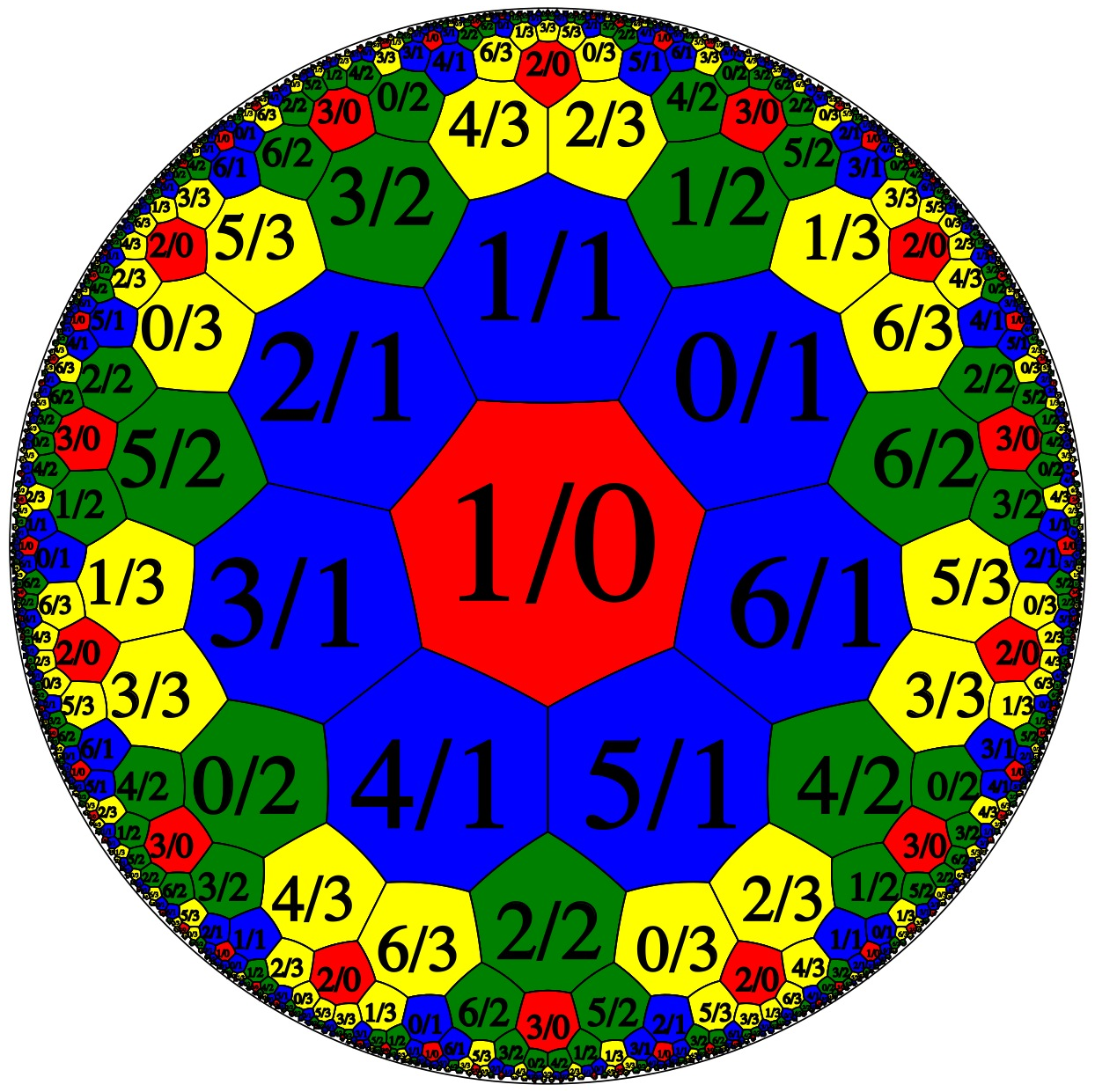
N = 7: coloured by denominator
Consider the faces with denominator , coloured red. There are three of these: , and . Each is surrounded by a uniformly coloured ring: by a blue ring of faces with denominator , by a yellow ring of faces with denominator , and by a green ring of faces with denominator .
Consider the group of units in , viz. . After modding out by , we can pick representatives . In , we can represent the actions on fractions, which result in multiplying denominators by these units , , and , respectively, by the matrices , and .
For instance, multiplying the above picture by , we get the following:

N = 7: denominators multiplied by 2
Here is what we are seeing: each of the three different kinds of face is the centre of a block, consisting of itself together with the ring of faces surrounding it, all of which have, as denominator, the unit ). And under the action of the group of units, each such block gets sent to another such block.
Let’s just show those blocks, each in its own colour, and outlined with thickened edges, grouped by still thicker edges into adjacent triplets, each corresponding to the entire quotient space.

N = 7: coloured by block
Or, bringing out the unit group action more clearly as a symmetry:

N = 7: coloured by block, symmetrical
In general, for an odd prime, we always get a version of the pattern we have seen for and . There will be units in , (just as there are units in ). These will give a “rescaling group” with elements. (The elements are units mod —just as the rescaling group mod consists of , as we say above).
The modular curve will be made up of blocks of -gons, corresponding to the elements of the rescaling group—just like the blue, yellow and green blocks for .
Each block will itself consist of a central face (for some unit ), surrounded by faces with denominator .
There will be orbits of the rescaling action in total: one including (and all the other -denominator fractions), and then one for each fraction of the form (including this fraction together with its images with different denominators, viz. other units-mod-).
When is not prime, the surface doesn’t divide up quite so neatly, but luckily things are not too different. However, since I’ve been talking for a while, I think I’ll leave that for next time.
