Farey Sequences and the Stern-Brocot Tree
Posted by John Baez
guest post by Tim Silverman
I want to discuss in more detail the modular curves , and , that is, the quotients of the upper half plane by , and respectively (with cusps filled in). These are charismatic entities — for example, you may have seen Greg Egan’s movie of , also known as Klein’s quartic curve:
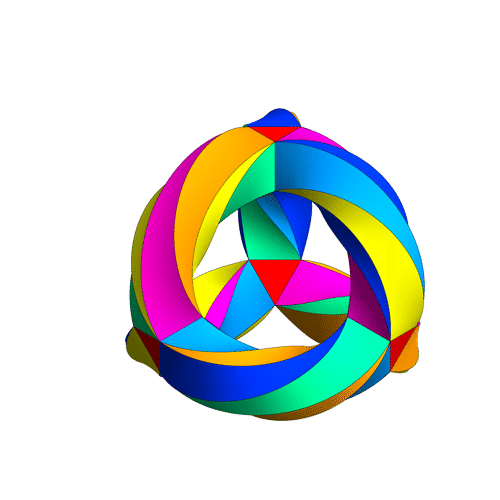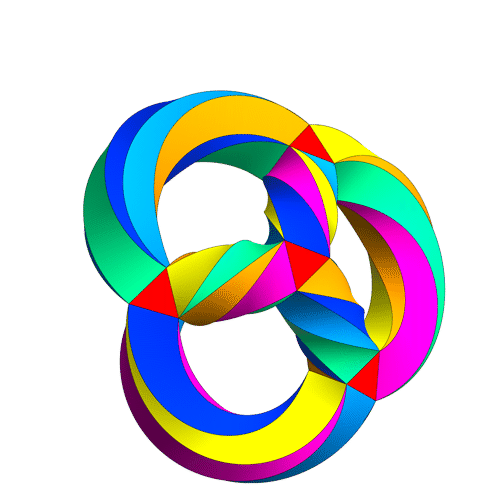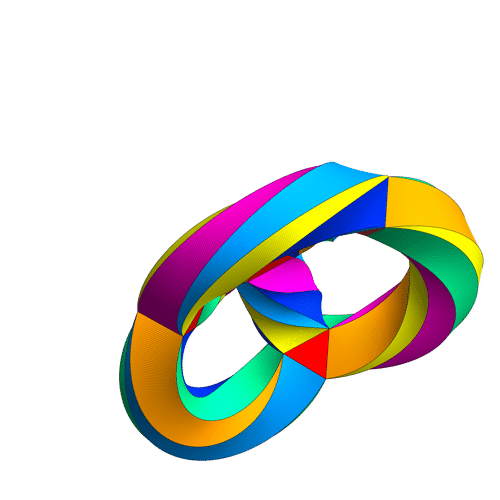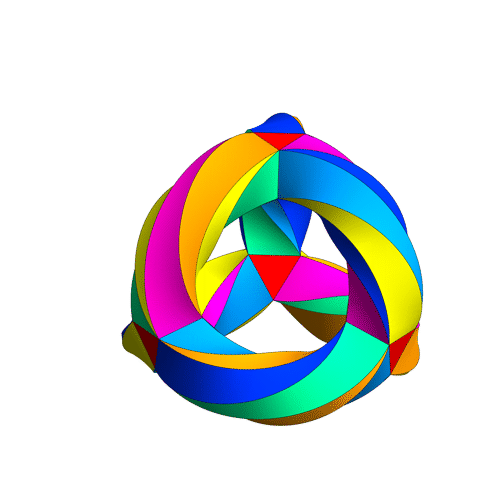
I also want to talk about the actions of the Hecke operators and on modular forms—or at least the corresponding actions on modular curves. Alas, I don’t think I’m going to get there in this post, but I can at least make a start.
But before I talk about all that, I want to talk about Farey sequences!
I was introduced to Farey sequences by a maths teacher at school, when I was about 13 or so, one afternoon when I’d done all my work and was feeling bored. They’re a simple and cute idea, and I found them kind of fascinating, but, not being much of a number theory person, I never looked into them all that deeply. But one stumbles across these things in the oddest places.
What is a Farey sequence? It’s very simple. Take all the reduced fractions from 0 to 1 (inclusive) with denominators no larger than some maximum . Now arrange them in order of increasing value. And that’s a Farey sequence. Thus Farey sequences include
and so on. Here’s the ninth Farey sequence:
There are some curious facts about Farey sequences. Here’s one: if and appear adjacent to one another in some Farey sequence, then .
Here’s another: if and appear adjacent to one another in some Farey sequence, then the next fraction which gets inserted between them, as you work your way through the successive Farey sequences, is the fraction . This funny combination is called the mediant of and , since it always lies between them. By repeatedly taking mediants, we build up all Farey sequences, and hence get each rational number from to exactly once.
We can indicate the way that the mediant derives from two parent fractions by drawing lines from the parents to their mediant:
A Farey sequence in tree form
Additionally, one of the parents must always derive from the other—it must have been inserted as a mediant itself at some earlier time. So if a fraction is connected to its parents by a pair of lines, the parents must also be connected to each other. So these lines actually make up a bunch of triangles, except at the top of the picture where everything starts. Taking the three numbers at the vertices of a triangle, any one of them can be derived from the other two either as their mediant, , or as what we might call their ‘mediant difference’, . In fact every pair of numbers joined by a line belongs to two triangles (one on either side of the line joining them), and one of the triangles will contain their mediant as its third point, while the other will contain their mediant difference instead!
So, can the Farey tree be extended to include fractions outside the interval ? That’s something we might be wondering, and the answer is Yes! In fact, this would have happened already if we hadn’t foolishly forgotten something: we’ve included fractions with denominators of , , , etc, but we’ve forgotten to include fractions with denominator ! How could we have been so careless? Let us remedy this oversight at once!
Including the fraction right at the top of the tree, it turns out that we can actually derive from this together with , as their mediant, and then we can get from and , and so forth, and by building up mediants, we can get all non-negative rational numbers that way. The whole tree is called the Stern-Brocot tree.
A piece of Stern-Brocot Tree
Once we’ve made these extensions, and added an edge connecting and , we see that every fraction in the tree, including the ones right at the top, belongs to a triangle—in fact, it belongs to an infinite number of triangles! We can just keep forming new mediants from it with its new neighbours forever. However, an infinite number of triangles hanging off every vertex is rather unmanageable. Is there some way we can get a toy version, with only a finite number of triangles instead? For instance, suppose we mod out the fractions by some natural number ? That is, we mod out both numerator and denominator by , taking care not to forget that ? Then many different -fractions will map to the same -fraction, and if we identify the corresponding points, and also, of course, identify the corresponding edges connecting corresponding points, then we will get something finite.
For instance, suppose we take the above tree mod (reducing the fractions where necessary to their lowest form, and bearing in mind that , so ). We get this:
A piece of Stern-Brocot Tree Mod 3
Or reducing mod (and bearing in mind that and , we get this:
A piece of Stern-Brocot Tree Mod 4
The rule about mediants and mediant differences still applies, but sometimes, with all the swapping of signs, we’ve switched around which fraction relates to which how!
Anyway, with these trees in hand, all we need to do is identify the vertices and edges correctly, and we’ll get something interesting and finite. In fact, while we’re about it, why not fill in those triangles? Then we’ll get a compact surface! It will be triangulated, and in fact each vertex will be the apex of just triangles (this is completely obvious in the case of the vertex , but it applies to all vertices). Or, dually, every vertex will stand at the centre of an -gon, while each of the triangular faces gives rise, dually, to a vertex at which -gons meet.
Wait a minute …
That sounds familiar …
Could it be … ?
Yes it is! The compact surface we have just constructed is none other than , the quotient of by . Quel surprise! The fractions mod correspond to the cusps, and we can make the dual tiling completely regular if we pick the right constant-curvature metric (which will need positive curvature for , negative curvature for , and will have to be flat for ).
In fact, this also works for the full Stern-Brocot tree, without any modding out, with fractions over all integers. We can see this either arithmetically or geometrically.
Arithmetically, replace the fraction by the element in . Of course, acts on this by ordinary matrix multiplication; indeed, acts on it too, more nicely, since switching the signs of both numerator and denominator doesn’t affect the value of the fraction.
In particular, if we pick an element of such as
then those two starting fractions at the top of the tree, and , will get sent, under the action of that group element, to a pair of fractions and such that . (That minus sign is a result of listing the fractions the ‘wrong’ way around). This same relation holds true of any two adjacent elements in a Farey sequence, and since some member of is available to send and to any adjacent pair, we get all Farey sequences in this way—over all integers, not just in the interval .
Now, and are joined to each other by an edge, and, being adjacent elements of a Farey sequence, so will their images be. In addition, each of and is also joined by an edge to , their mediant. But the mediant of fractions corresponds simply to the sum in (considered as a -module). And obviously the sum relation is preserved by . So if gets sent to and gets sent to , then gets sent to the mediant of and , meaning that the other two sides of that top triangle -- are also preserved—sent to sides of a triangle in the image.
So triangles are sent to triangles. Moreover, since the relation of being the mediant (or sum) of the other two vertices—as opposed to their mediant difference (or difference)—uniquely picks out one vertex of a given triangle, and since the sign of the determinant—or, more simply, which of the parent vertices is larger—uniquely picks an orientation of the triangle, each triangle is sent to another triangle in only one way. So acts freely on the set of triangles, and of course preserves their relations.
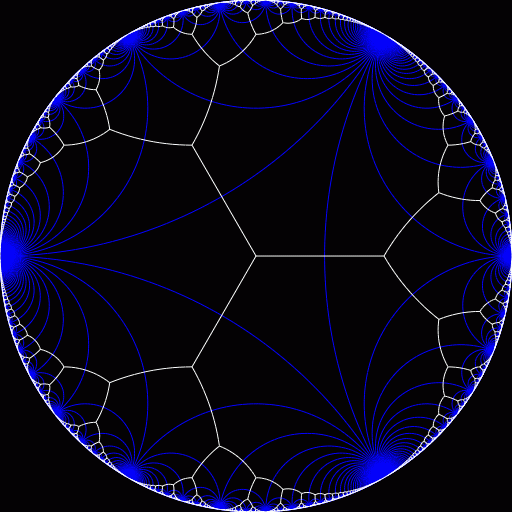
Geometrically, as we can see from Don Hatch’s nice Hyperbolic Tesselations web page, the tilings of the hyperbolic plane by regular -gons, meeting at each vertex, have a limiting case with a tiling by what one might call regular -gons, or regular -gons, with an infinite number of sides! They appear in the website as {infinity, 3}:
Dually, we get a tiling by triangles, an infinite number of which meet at the ‘centre’ of each -gon. These triangles correspond precisely to the triangles in the Stern-Brocot tree. Rather confusingly, however, in the Poincaré disk model, the ‘centre’ of a -gon appears at the edge of the disk—that’s the sort of thing that happens when you have an infinite number of sides and are trying to show them all in a bounded region.
If we compare the Poincaré disk model of the hyperbolic plane with the ‘upper half-plane’ model, we see that the real line of the latter goes to the boundary circle of the former. The -gons, drawn in the Poincaré disk, are all tangent to the boundary circle, each with its own distinct point of tangency, and these points correspond precisely to the rational numbers (together with ). In turn, these rational numbers are the ones in the Stern-Brocot tree, i.e. at the vertices of the triangles, which can also be seen as tiling the hyperbolic plane, dually to the -gons. In this way, we also get to label each -gon by a unique rational number, and this is inherited when we go over to the version mod —fractions also being reduced mod .
Given all this, one way to try and understand the way that geometry and arithmetic interact in is by working our way down the Stern-Brocot tree mod , which will correspond to working our way outward from one of the -gons in . What we’re going to see is a series of concentric circles of fractions with successively incrementing denominators.
But that, I think, is something for another post.


Re: Farey Sequences and the Stern-Brocot Tree
There seems to be a lot of beautiful classical geometry connected to such locally symmetric spaces, e.g. MacPherson and McConnell construct in:
“Classical projective geometry and modular varieties”, in “Algebraic analysis, geometry, and number theory” (Baltimore, MD, 1988)
cell complexes equivalent to (compactified) locally symm. spaces from configurations of projective geometry:
“Classical projective geometry was a beautiful field in mathematics. It died, in our opinion, not because it ran out of theorems to prove, but because it lacked organizing principles by which to select theorems that were important. Also, it was isolated from the rest of mathematics. Much of what we do may be regarded as direct continuation of nineteenth century synthetic geometry. In fact, we hope the new motivation of studying C-complexes will provide projective geometry with one organizational principle, and with one relation tying it to “mainstream” mathematics. We note … representable matroids, arrangements of hyperplanes, and motivic cohomology. A large part of this paper’s exposition is motivated by this dream of continuing classical projective geometry.”
Here is a related overview.