Enrichment and the Legendre-Fenchel Transform II
Posted by Simon Willerton
Last time, I described the Legendre-Fenchel transform. For a real vector space , the transform gives a bijection between the convex functions on and the convex functions on its dual . This time I’ll show how this is naturally an example of the profunctor nucleus construction in enriched category theory.
The key to this relationship is that the natural pairing between a vector space and its dual can be thought of as profunctor between discrete -categories, where is the extended real numbers thought of as a closed, symmetric monoidal category.
As I’ll explain, we can then apply the machinary of the nucleus construction to get a pair of maps between the -presheaves on , which just means the -valued functions on , and the -copresheaves, ie the -valued functions, on . Restricting to the part on which the pair of maps is bijective, we get that the transform gives a bijection between the respective sets of convex functions.
This category theoretic treatment gives us a little more than the standard treatment. Usually people put an ordering on the functions and observe that Legendre-Fenchel transform is order reversing. The category theory tells us that we can refine this and put a generalized, generalized metric space structure on the space of functions so that the transform is distance non-increasing, and is in fact distance preserving in the case of convex functions. This is illustrated by the above picture, as we will discover below!
1. Enriching over the extended real numbers
The basics
We will be thinking about enriched categories over , the extended real numbers. We make into a category by using the ordering , so there is a morphism if and only if . (The opposite ordering is considered in Lawvere’s paper State categories, closed categories, and the existence of semi-continuous entropy functions.)
We make into a symmetric monoidal category using addition ‘’ and we can use subtraction ‘’ as the internal hom to make it into a closed symmetric monoidal category: this is because It’s important here to note how this arithmetic extends to the infinite elements, in particular, despite notational appearances, is not the additive inverse of , indeed is a rather ambiguous thing to write as Full addition and subtraction tables can be found in the nice Bachelor’s thesis of Soichiro Fujii.
We’ve got a closed symmetric monoidal category so we can consider categories enriched over . An -category is a generalized, generalized metric space!
Remember that a generalized metric space in the sense of Lawvere is like a metric space but the main difference is that we don’t impose that the ‘distances’ are symmetric, so in general .
An -category is further generalized in that we allow negative ‘distances’. For want of a better name, these generalized, generalized metric spaces I will call ‘-spaces’. This means that an -space is a set with a function such that
for all ;
for all .
Putting into the second inequality gives that is either or , with latter only possible if and are infinite for every .
An example of an -space is equipped with -distance If you know about the Hilbert metric you might wish to think how this is related.
Vector spaces
Now suppose that we have a real vector space . We think of this as a discrete -spaces so that for and . Similarly, we think of the dual vector space as a discrete -space. The tautological pairing can be considered as an -profunctor between these -spaces.
We can now interpret what the -spaces of presheaves and opcopresheaves on our vector spaces are. As the vector spaces are considered as discrete -metric spaces the -space of presheaves on and the -space of opcopresheaves on , will just be the sets of -valued functions with no constraints on them, the interesting pieces of structure are the metrics: The distance from a function to a function is the most that you have to go ‘up’ from to get to , where going down means going ‘up’ a negative amount.
For example, for the functions illustrated at the top of the post we have and The fact that these distances coincide is not mere coincidence, as we shall below.
2. The nuclear construction
Now I will remind you of the general construction of profunctor nucleus (this needs a better name!) that I blogged about last year. We start with a -profunctor between two -categories and obtain a duality between certain subcategories of presheaves on one category and copresheaves on the other. In practice, these often turn out to be interesting dualities.
For instance, if we work over the monoidal category then a profunctor between discrete categories amounts to a relation between sets, whereas a presheaf amounts to a subset, so from a relation between between sets you get a bijection between certain distinguished sets of subsets. This underpins many dualities in mathematics. Here is a classic example.
- Suppose we take one set to be , the other set to be polynomials in -variables, and take the relation to be that is related to if . Then the resulting duality is the classical algebraic geometry correspondence between algebraic subsets of and radical ideals of .
I should remind you what process leads us here. Starting with a closed symmetric category , two -categories and , and a profunctor between them, we obtain an adjunction between presheafs on and opcopresheaves on . The left and right adjoints can be given by end formulas: for instance if is a presheaf on then The nucleus is defined as the centre of this adjunction. This means that it consists of the induced isomorphism between the part on which the monad is an isomorphism and the comonad is an isomorphim.
3. The synthesis
We can now feed our vector space pairing in to the profunctor nucleus machine. What pops out of the machine first is an -adjunction between function spaces: We can denote both of the maps by asterisks, and we find that both of them have the same form, so for a function on and a function on we find These are, of course, precisely the Legendre-Fenchel transform and its reverse!
The standard theory of the profunctor nucleus tells us that and This means that if we restrict to the image inside then we get an isomorphism. The image consists of the (lower semi-continuous) convex functions, so we get This is the usual Fenchel-Legendre duality.
From our machine we get a little more than this. As we have an adjunction we know that : spelling that out we have the following theorem.
Theorem: Suppose that we have functions and then
I would welcome any nice interpretation of this result!
On top of that, we know that the transform is a distance non-increasing map so we have . Spelling this out as well gives the following.
Theorem: Suppose that we have functions then
As the reverse transform is also distance non-increasing, and as we know that when is convex, we get the immediate corollary that distance is preserved for convex functions.
Corollary: Suppose that we have (lower semi-continuous) convex functions then , in other words,
This is illustrated by the example at the top of the post (click for a larger picture), where we have already observed that
This -metric on the space of (convex) functions seems to be overlooked in literature that I’ve seen. (In many cases the distance between convex functions will be infinite.) However, people do consider the partial order on the set of convex functions: when for all . The -distance is a refinement of this partial order in the if and only if .
The standard fact that the Legendre-Fenchel transform is order reversing is then a corollary of the above corollary: in other words we get that for convex functions we have
If anyone has seen these -metrics being used in this context I’d be happy to hear about it.
Anyway, the encroachment of category theory into analysis continues…

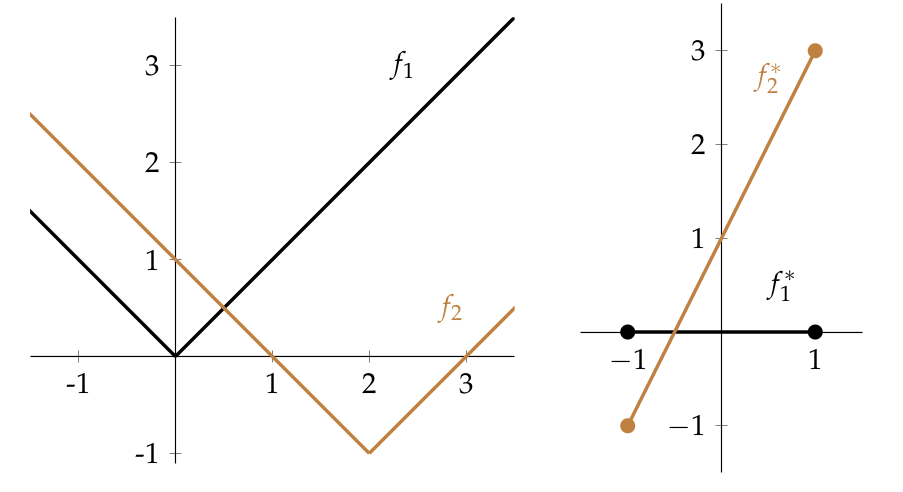
Re: Enrichment and the Legendre-Fenchel Transform II
Nice post!
The corollary (with an arbitrary function) is called Toland–Singer duality, and seems to be known in the field of continuous optimization. But the simpler first theorem yields it immediately and it’s pleasant that the theorem is just the adjunction isomorphism!